Глава 12. Расчеты ожидаемой эффективности проекта

503

Так, если имеются независимые наблюдения ь_х,..., ь_т случайной величины, распределение которой имеет плотность р(р, в), зависящую известным образом от неизвестного скалярного или векторного параметра 0, то правдоподобие какой-либо оценки 0* этого параметра характеризуется произведением р^, 9*)* ...• р(р_т, 0*). Математическая статистика рекомендует при этом принимать в качестве наиболее точной оценки неизвестного параметра его наиболее правдоподобное значение, на чем и основаны почти все методы статистического оценивания.

ПРИМЕР 12.20. Время задержки платежа за поставленную продукцию рассматривается как случайная величина, имеющая экспоненциальное распределение, — вероятность того, что длительность задержки превысит I, при положительных I равна е'¹^. Таким образом, плотность этого распределения равна 0~'е~'/^е. В расчет эффективности решили заложить среднюю длительность задержек, для данного распределения она равна 0. Для определения 0 использованы следующие данные о фактической длительности задержек десяти платежей в днях: 8, 17, б, 45, 39, 32, 11, 51, 21, 37. Плотность вероятности для фактически наблюденных значений задержки определится теперь как произведение

(г¹*-^ Ид-'е-^ ]= 0-'V²⁶⁶/".

Само это выражение не очень удобно для графического представления. Однако легко проверить, что наиболее правдоподобным будет значение 0 = 226/10 = 26,6. При этом функция правдоподобия примет наибольшее значение (26,6е)~¹⁰. Разделив значения функции правдоподобия на ее максимальное значение, получим, что относительное правдоподобие того или иного значения 9 может быть задано формулой

-,10 26,6 1-26,6/9

о ^е . График этой функции приведен на следующем рисунке.

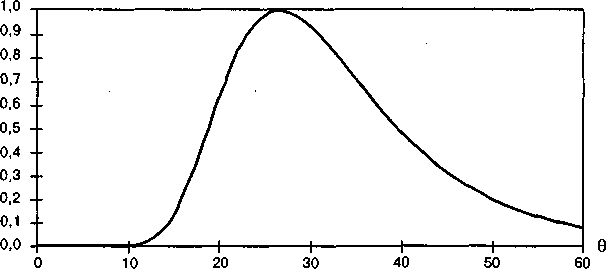
504 Часть I. Теоретические основы оценки инвестиционных проектов

Таким образом, ориентироваться только на наиболее правдоподобное значение 6 было бы не слишком реалистично — любые значения 6 в пределах, например, от 20 до 35 представляются также достаточно правдоподобными, для того чтобы их можно было использовать в расчетах. Поэтому в данной ситуации следовало бы оценить проект при разных значениях 6, учитывая при этом степень их правдоподобия.

Мы не будем подробно останавливаться на математико-статистичес-ком происхождении функций правдоподобия и их использовании в статистике, адресуя читателей к [41] и другой литературе по этим вопросам. Дело в том, что математическая статистика — не единственный источник приписывания определенной степени правдоподобия тем или иным явлениям или числам.

ПРИМЕР 12.21. Иванов на работе обычно молчит. Однако сослуживцы заметили, что если он выпивает, то на следующий день становится очень разговорчивым. Сегодня Иванов необычайно разговорчив. Поэтому весьма правдоподобно, что вчера он выпивал.

»

ПРИМЕР 12.22. В прессе появилось множество интервью с представителями экономических ведомств о том, что проведение денежной реформы в существующих условиях нецелесообразно. Рядовой гражданин делает из этого однозначный вывод о том, что проведение такой реформы в ближайшее время весьма правдоподобно.

ПРИМЕР 12.23. Из баланса предприятия видно, что дебиторская задолженность невелика. Тем не менее рабочим длительное время не выдают заработную плату, ссылаясь на то, что покупатели не оплатили поставленную продукцию. Поэтому весьма правдоподобно, что в балансе допущены ошибки.

Таким образом, рассматривая какие-то значения неопределенной величины или какие-то возможные события, мы приписываем им (возможно, не отдавая себе в этом отчет) определенное число, выражающее степень их правдоподобия. При этом нам обычно не важно, в каких единицах, в каком масштабе это правдоподобие измерено, поскольку нам необходимо лишь сравнивать разные числа или события по степени их правдоподобия. В этих условиях естественно договориться о том, что наиболее правдоподобному числу или событию будет приписана степень правдоподобия, равная единице, а всем остальным — какая-то меньшая, но неотрицательная степень. Невозможным значениям неопределенной величины или невозможным событиям (в примере 12.21 — "Иванова назначили премьер-министром") естественно приписать нулевую степень правдоподобия.