Глава 12. Расчеты ожидаемой эффективности проекта

501

1,0 -г 0,8 --0,6 --0,4 --0,2 4-) 0,0

■В 0,0

800 900 1000 110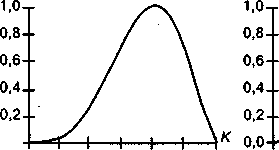0

720 740 760 780 800 820 840

Н 1 1-

0,4 0,42 0,44 0,46 0,48 0,5

Степень принадлежности, равная единице, отвечает базовым значениям параметров: В = 900, К = 800, у = 0,47. В этом случае эффект проекта, рассчитанный по приведенной формуле, составит 240,7 и ему будет отвечать степень принадлежности, равная единице.

Производя методом Монте-Карло перебор других сочетаний возможных значений параметров проекта и определяя их степень принадлежности (по каждому сочетанию она равна наименьшей из степеней принадлежности для В, К и у), можно построить и функцию принадлежности для нечеткого ЧДЦ, представленную на следующем рисунке, — из-за того, что перебирались не все возможные сочетания, она оказалась не слишком "гладкая".

1,0 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0,0

-400-300-200-100 0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500

Примем следующие допущения:

• значения эффекта, имеющие степень принадлежности менее 0,1, не учитываются;

• случайные величины ^их\ имеют одно и то же распределение на отрезке [0,1, 1] с плотностью р(х) = 2(х - 0,1)/0,81;

• параметр "оптимизма-пессимизма" X = 0,3.

Используя полученный график, можно рассчитать ^-максимальное и ^-минимальное значения нечеткого эффекта при разных % и г\ и с помощью стандартных программ численного интегрирования найти их математические ожидания: М^[М(^Л)] = -23,3; М_л[т(т1,>1)]= 178,2. Теперь ожидаемый эффект проекта находится по формуле (12.14)

502

Часть I. Теоретические основы оценки инвестиционных проектов

Э_ож(А) = Ш^[МЙ,Л)]+(1-А.)М_п[т(т₁,Л)] = 0₁7х(-23₎3) + 0,Зх178,2 = 154,9.

Как видим, расчет с учетом неопределенности дает более "осторожное" значение ожидаемого эффекта по сравнению с расчетом по наиболее возможным, базовым значениям параметров.

В заключение следует отметить, что для ситуации интервальной неопределенности критерий (12.14) совпадает с критерием Гурвица (12.6).

12.7. """Проекты с эффектом, наделенным правдоподобием

Многое из того, что мы называем менеджментом, заключается в том, чтобы усложнить людям работу.

Питер Ф. Друкер

При разработке проектов нередко возникают ситуации, когда какой-либо параметр проекта определяется на основе статистической информации. Любые значения параметров, которые при этом получаются, не могут рассматриваться как абсолютно достоверные. Приведем простой пример.

ПРИМЕР 12.19. Расход сырья на единицу готовой продукции по четырем аналогичным предприятиям составляет 20, 23, 25 и 24 единицы. В проект предполагается заложить среднее арифметическое значение. Однако фактические удельные расходы отклоняются от средних — соответствующее среднеквадратичное отклонение равно

^[(20-23)² + (23-23)² + (25-23)² + (24-23)²]/4=Д5=1,9.

Что же означает полученный результат? Если считать, что наблюдаемые значения расхода имеют нормальное распределение и ограничиться доверительным уровнем 95%, то отсюда следует, что истинное значение среднего расхода может отличаться от рассчитанного примерно на 4 единицы в обе стороны. Но следует ли из этого, что расход 27 следует заложить в расчет с тем же основанием, что и расход 23? Нет, не следует. Вероятность наблюдать значения 20, 23, 25 и 24 при среднем расходе 27 намного меньше, чем при среднем расходе 23. В математической статистике в этих целях используется выражение "менее правдоподобно", а соответствие между принятым уровнем какого-либо параметра и наблюдаемыми реализациями зависящих от него других величин характеризуют величиной правдоподобия.