Часть I. Теоретические основы оценки инвестиционных проектов

значениях нормы дисконта интегральный эффект отрицателен. В математических терминах последний пример приводит к кратному (в данном случае — двойному) корню. Если же в данном проекте уменьшить денежный поток на шаге 2 до -17, то уравнение Ф_инт(йГ) = 0 приводится к виду 10х² - 2бх + 17 = 0. Последнее уравнение вообще не имеет вещественных корней (его корни — комплексные величины). Поэтому приведенный в примере денежный поток ВИД иметь не может.

Попытка найти ВИД для проекта 3 приводит к уравнению 10х² + 2<Ьх -- 16,5 = 0. Хотя это уравнение и имеет положительный корень х_х ~ 0,528, соответствующее ему значение й_х = х_х - 1 < 0, и поэтому й_х не является ВНД. У этого проекта ВНД тоже отсутствует.

\+а

ос Наконец, для проекта 4 интегральный эффект Ф_инт = -10-

16,5

₂. Сразу ясно, что при любых неотрицательных нормах дисконта он отрицателен, и поэтому ВНД такой проект также иметь не может.

Что касается проектов второй группы, то ни один из них не может иметь ВНД. Если для денежных потоков этих проектов существует единственный простой положительный корень с1₀ уравнения Ф_инт(й9 = 0, интегральный эффект отрицателен при нормах дисконта, меньших с1₀, и положителен при нормах дисконта, превышающих с1₀, что противоречит определенным выше свойствам ВНД. Все остальные случаи (отсутствие корней, существование нескольких корней, кратные корни) рассматриваются так же, как и для проектов первой группы.

'Перейдем теперь от примера к описанию общей ситуации. Здесь могут возникнуть такие ситуации, показанные на рисунке:

I

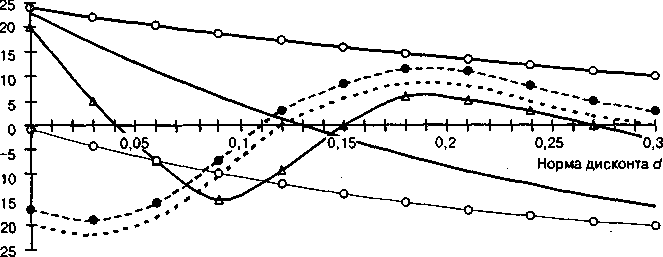
."Типичная" ситуация —Ситуация 3

> Ситуация 1 ■ Ситуация 4

Ситуация 2 Ситуация 5

Глава 8. Интегральные характеристики денежного потока

299

1) при всех положительных значениях а" функция Ф_инт(с1) положитель на. Так может быть, если проект начинается и заканчивается денеж ными поступлениями, а расходы осуществляются "в середине";

2) функция Ф_инт(й) положительна при малых положительных значе ниях а", но имеет несколько корней;

3) при всех положительных значениях а" величина Ф_инт(йО отрица тельна. Так может быть, если проект начинается с расходов и за канчивается расходами, тогда как доходы имеют место "в середи не проекта";

4. функция Ф_инт(й) отрицательна при малых положительных значениях й, но при увеличении й она становится и остается положительной;

5. функция Ф_инт(йО отрицательна при малых положительных значениях й, но имеет несколько корней.

Выше мы определили понятие ВНД только для "типичной" ситуации. Хотелось бы, однако, определить ВНД и для других ситуаций, чтобы сравнение ее с нормой дисконта позволяло не ошибаться в заключениях как об эффективности, так и о неэффективности проектов. Далее мы покажем, что это можно сделать только тогда, когда функция Ф_ИШ(с1) правильная в смысле п. 8.2.2 — каким бы способом ни определялась ВНД при неправильных Ф_инт(й!), это всегда может привести к ошибочным решениям.

В ситуации 1 проект будет эффективен при любой норме дисконта. Это значит, что ВНД > й при любом положительном а\ Ясно, что таким значением ВНД может быть только бесконечно большое (ВНД = + °°). В ситуации 3 проект будет неэффективен при любой положительной норме дисконта. Это значит, что ВНД < й при любом положительном а\ Ясно, что таким значением ВНД может быть только нулевое (для придания ситуации большей математической строгости можно принять ВНД = -1).

Сложнее обстоит дело с ситуациями 2, 4 и 5 (они имеют место для проектов, прекращение которых требует значительных ликвидационных затрат, скажем, для проектов создания АЭС). Здесь функция Ф_инт(й) имеет несколько корней, и нам удобно разделить их на три группы. Для этого заметим, что. изменение знака функции Ф_ИШ(сГ) при переходе через корень г определяется знаком ее производной. Для правильных функций Ф'_инт(г) < 0. Такие корни назовем нормальными. Если в точке г график функции Ф_инт(^) пересекает ось абсцисс "снизу вверх", то Ф'_инг(г) > 0. Такие корни назовем аномальными. Наконец, если этот график касается оси абсцисс в точке г, то Ф'_инт0*) = 0; такой корень назовем двойным. Последний случай крайне редок. Тем не менее, говоря о нем, отметим, что выбирать двойной корень в качестве ВНД мы не рекомендуем: при небольшом изменении проекта этот корень может стать "простым", но может и

300