§95. Пряма та обернена геодезичні задачі на площині

Вгеодезичній практиці часто необхідно розв’язувати дві задачі – пряму і обернену геодезичні задачі.

Пряма геодезична задача

Дано: координати першої точки Х₁ і Y₁ горизонтальну проекцію від першої до другої точки d і дирекційний кут лінії _1-2. Необхідно визначити координати Х₂ і Y₂ другої точки.

Спроектуємо точки 1 і 2 на осі координат (Рис.105). Проекції лінії d на осі Х і Y, очевидно будуть дорівнювати Х₂-Х₁=Х і Y₂-Y₁=Y. Різниця координат точок 2 і 1 називається приростами координат. З приведених формул можна написати, що Х₂=Х₁+Х Y₂=Y₁+Y

З прямокутного трикутника 1а2:

Х=dcos_1-2 Y=dsin_1-2

Отже, Х₂=Х₁+dcos_1-2

Y₂₌Y₁+dsin_1-2

В залежності від дирекційного кута, прирости координат можуть мати різні знаки. Знаки приростів координат визначаються знаками тригонометричних функцій sin і cos відповідної чверті.

Таблиця 6 показує залежність між дирекційними кутами і знаками приростів координат.

Таблиця 6

Прирости координат	Дирекційні кути
	від 0 до 90	від 90 до 180	від 180 до 270	від 270 до 360
	І чверть	ІІ чверть	ІІІ чверть	ІV чверть
Х Y	+ +	- +	- -	+ -

Обернена геодезична задача

Дано: координати Х₁ і Y₁ – першої точки і X₂ і Y₂ – другої точки. Необхідно знайти дирекційний кут лінії _1-2 і горизонтальну проекцію d між точками 1 і 2.

Знаюча координати першої і другої точок, можна визначити прирости координат: Х=Х₂–Х₁=dcos_1-2

Y=Y₂–Y₁=dsin_1-2

Очевидно, що в прямокутному трикутнику (Рис.105). 1а2 відношення Y до Х дозволяє визначити тангенс _1-2

Кут одержаний за тангенсом із таблиць натуральних значень тригонометричних функцій, буде табличним кутом (румбом) r_1-2. Для переходу від румба до дирекційного кута необхідно врахувати знаки приростів координат і визначити чверть (Таблиця 6) в якій розташований румб і від румба перейти до дирекційного кута. Визначивши дирекційний кут, можна визначити горизонтальну проекцію d за формулами:

;

Крім цього, віддаль можна визначити за теоремою Піфагора з прямокутного трикутника 1а2

§96. Обчислення зімкнутих теодолітних ходів

Перед тим, як приступити до обчислень теодолітних ходів, виконується перевірка обчислень в польових журналах. Після цього складають схему ходу і на ній виписують всі кути з журналу і горизонтальні проекції. Потім зі схеми кути переписують у відомість обчислення координат (Таблицю 7 графа 2).

Обчислення кутової нев’язки

В графі 2 підраховують суму всіх кутів, яку називають практичною сумою _П. Суму кутів _П порівнюють з теоретичною _т внутрішніх кутів многокутника, яка обчислюється за формулою: _т=180(n-2), де n – кількість кутів у зімкнутому теодолітному ході. Різниця між сумами _п і _т називається кутовою нев’язкою ходу “f”; f=_П–_т. Кутова нев’язка не повинна перевищувати величини f_доп=1, де n – кількість кутів теодолітного ходу, Якщо обчислена нев’язкаf не перевищує f_доп, то її розподіляють порівно в кожний виміряний кут з оберненим знаком, тобто . Після введення поправок “_К” у виміряні кути _П повинна дорівнювали _т.

Обчислення дирекційний кутів і румбів сторін зімкнутого теодолітного ходу.

Після виправлення кутів в теодолітному ході приступають до обчислення дирекційний кутів всіх його сторін. Якщо нам відомий дирекційний кут вихідної сторони АВ (Рис.106) і прилеглий кут ' то обчислюють дирекційний кут прилеглої сторони А-1.

Рис.106

Згідно з рисунком 106 можна написати:

_А-1=_АВ+'

_1-2+₁=_А-1+180

_2-3+₂=_1-2+180

або .............................

_1-2=_А-1+180-₁ (1)

_2-3=_1-2+180-₂

............................

з наведених рівнянь (1) можна написати: дирекційний кут наступної лінії дорівнює дирекційному кутові попередньої лінії плюс 180 і мінус правий за ходом кут і навпаки – дирекційний кут наступної лінії дорівнює дирекційному кутові попередньої лінії мінус 180 і плюс лівий за ходом кут.

_А-4=_1-А-180+_А (2)

При обчислені дирекційних кутів за формулами (1) і (2) бувають випадки, коли обчислений дирекційний кут може мати значення більше за 360, то такий дирекційний кут необхідно зменшити на 360. Якщо від дирекційного кута меншого за 180 необхідно відняти 180, то до зменшуваного слід додати 360. Для контролю правильності обчислення дирекційних кутів в кінці ходу знову обчислюють дирекційний кут сторони А-1 за допомогою кута _А, який не використовувався в попередніх обчисленнях дирекційних кутів.

Після цього за дирекційними кутами обчислюють румби всіх сторін ходу.

Обчислення приростів координат і лінійної нев’язки в приростах координат зімкнутого теодолітного ходу

Маючи обчисленні горизонтальні проекції сторін теодолітного ходу і їх дирекційні кути, користуючись формулами Х=dcos і Y=dsin обчислюють прирости прямокутних координат всіх ліній ходу.

Після обчислення приростів всіх сторін теодолітного ходу підраховують алгебраїчні суми приростів які називають практичними сумами, тобто _ХП і _YП.

Як відомо, прирости координат є проекціями сторін теодолітного ходу на осі координат і в зімкнутому многокутнику повинні дорівнювати 0 (Рис.107), тобто теоретична сума приростів на осі координат дорівнює 0

Х₁+Х₂+Х₃=0; _Х=0; Y₁+Y₂+Y₃=0; _Y=0

Р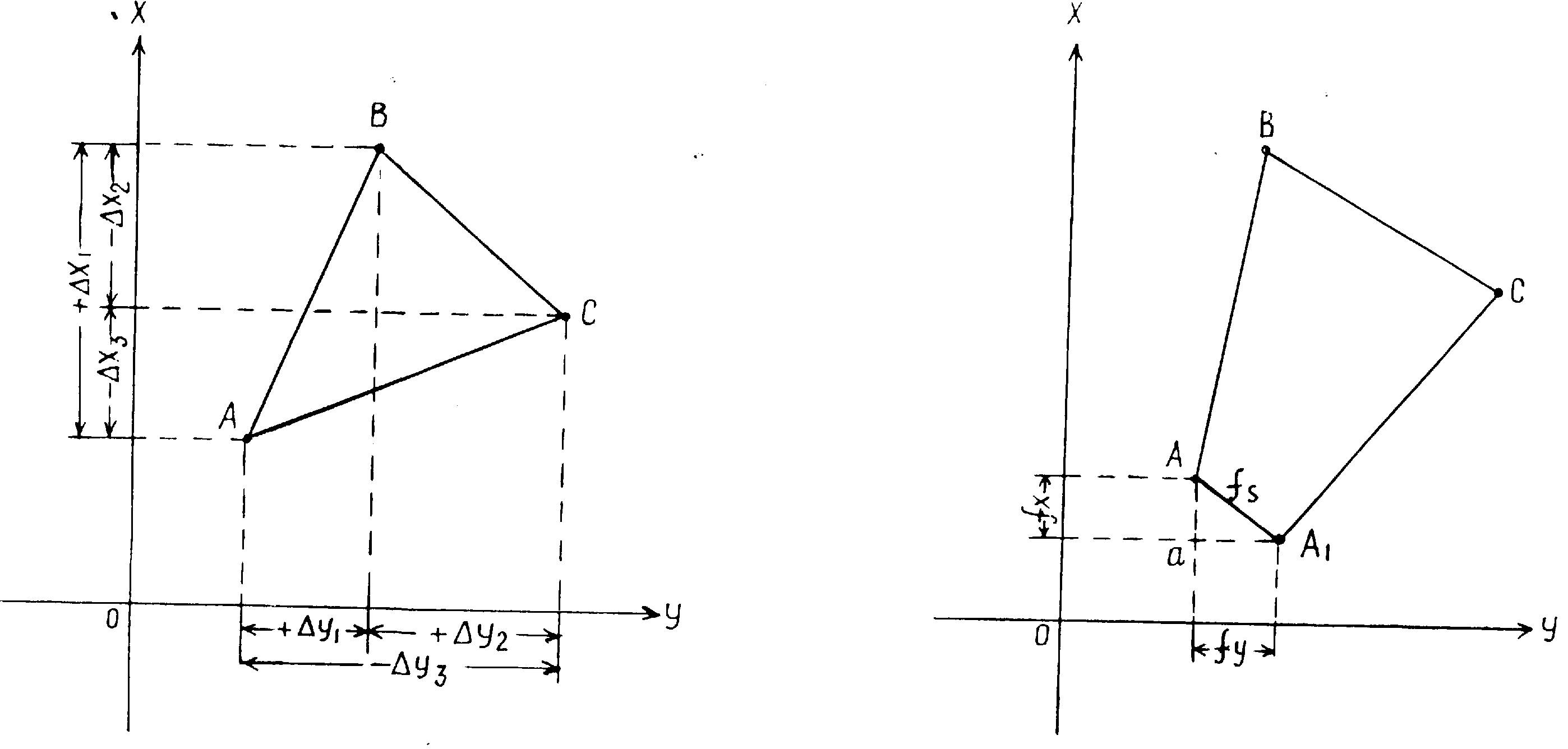ис.107 Рис.108

Але, внаслідок помилок при вимірюванні кутів і ліній ця умова виконуватись не буде і суми приростів по осях координат не будуть дорівнювати 0, а деяким величинам f_x і f_y тобто _xп=f_x; _yп=f_y. Внаслідок цього точка А (Рис.108) в кінці ходу займе інше положення, а саме А₁. Таким чином многокутник не зімкнеться на величину АА₁=f_s. Величина “f_s“ називається абсолютною лінійною нев’язкою, а f_x і fy – нев’язками в приростах координат. З трикутника АаА₁ обчислюють f_абс . На практиці користуються відносною лінійною нев’язкоюf_від, тобто відношенням f_абс до периметру полігона Р, або нев’язкою, що припадає на одиницю довжини ходу. Ця величина не повинна перевищувати довжини ходу. Якщоf_від перевищує допуск, то необхідно визначити місце в теодолітному ході, де допущена груба помилка при вимірюванні кутів, або ліній. Для цього за нев’язкими f_x і f_y слід визначити сторону ходу, в якій допущена помилка в довжині, або напрямку.

Згідно з рисунком 108 , – дирекційний кут напрямку нев’язки АА₁. За допомогою знаків визначають назву румба, а за румбом дирекційний кут напрямку нев’язки АА₁. Порівнюючи дирекційний кут напрямку нев’язки з дирекційними кутами сторін теодолітного ходу, знаходять сторони дирекційні кути, яких близькі до дирекційного кута нев’язки. Після цього перевіряють обчислення приростів координат пов’язаних з цими дирекційними кутами і коли не знаходять помилок в обчисленнях, то повторюють відповідні вимірювання на місцевості.

Якщо відносна нев’язка не перевищує допуск, то нев’язки в приростах координат розподіляють по приростах пропорционально до довижин ліній з протилежним знаком так, щоб після розподілу нев’язок суми приростів координат дорівнювали “0”, тобто _Хп=0; _YП=0. Для цього визначають поправку на 1 метр довжини лінії. З цією метою величини нев’язок ділять на периметр полігона ,, а потім визначають поправку на всю довжину лінії;. В тих випадках, коли нев’язкиf_x і f_y за абсолютною величиною малі, то обчислюють поправки не на 1 м довжини лінії, а на 100 м, тому що на 1 м ці поправки дуже малі, тоді ;.

Додаючи алгебраїчно обчислені поправки _xi_yiдо обчислених приростів координат, одержимо виправлені прирости координат.

;

;

В приведених формулах:

; ... обчислені прирости координат

; ... обчислені прирости координат

; ... виправлені прирости координат

; ... виправлені прирости координат

Сума виправлених приростів координат в зімкнутому полігоні повинна дорівнювати “0”, тобто теоретичній сумі приростів.