Операции над комплексными изображениями гармонических функций

Определим операции над комплексными амплитудами, соответствующие ли нейным операциям (см. модуль 2.1) над гармоническими функциями времени.

Найдем комплексную амплитуду функции a(t) = α · a1(t), полученной путем ум ножения гармонической функции а1(t) = Аm1 cos(ωt + ψ1) на вещественное число α. Очевидно, что

Таким образом, умножению гармонической функции времени на произвольное число соответствует умножение комплексной амплитуды на это же число:

. 2.36

Определим комплексное изображение суммы гармонических функций времени a1(t), a2(t), ..., aN (t) одной частоты ω с комплексными амплитудами m1, m2, …, mN. В соответствии с (2.34) получаем

Следовательно, суммированию гармонических функций времени одной часто ты соответствует суммирование комплексных амплитуд:

. 2.37

Из выражений (2.36) и (2.37) следует, что линейной комбинации гармониче ских функций времени одной частоты соответствует линейная комбинация их ком плексных амплитуд:

,

где αk— постоянные коэффициенты; N — произвольное целое число.

Найдем комплексное изображение производной гармонической функции вре мени a(t):

Таким образом, дифференцированию гармонических функций времени соот ветствует умножение их комплексных амплитуд на jω:

104

Определим комплексное изображение интеграла от гармонической функции времени a(t):

Следовательно, интегрированию гармонических функций времени соответст вует деление комплексных амплитуд на jω:

Линейным операциям над гармоническими функциям времени соответст­ вуют линейные операции над их комплексными амплитудами, причем опера­ ции дифференцирования и интегрирования заменяются операциями умноже­ ния и деления. Эти свойства комплексных изображений гармонических функ­ ций позволяют существенно упростить анализ линейных цепей, находящихся под гармоническим воздействием, так как дают возможность замешать систему интегродифференцнальных уравнений электрического равновесия цепи, со­ ставленную для мгновенных значений токов и напряжений ветвей, системой алгебраических уравнений для комплексных амплитуд соответствующих токов и напряжений.

Наряду с комплексной амплитудой Аm в качестве изображения гармонической функции a(t) в комплексной плоскости широко используют другую комплексную величину — комплексное действующее значение . По определению, комплексное действующее значение гармонической функции времени a(t) = √2· A∙cos(ωt+ψ) представляет собой комплексное число , модуль которого равен действующему значению А гармонической функции, а аргумент — ее начальной фазе ψ

. 2.40

С помощью выражений (2.12) и (2.32) можно установить связь между ком плексной амплитудой гармонической функции a(t) и ее комплексным дейст вующим значением :

направлению с вектором . Длина вектора в √2 раз меньше длины вектора .

105

Все правила, устанавливающие соответствие между операциями над гармони ческими функциями времени и операциями над их комплексными амплитудами, справедливы и для операций над комплексными действующими значениями гармо нических функций.

Комплексные сопротивление и проводимость пассивного участка цепи

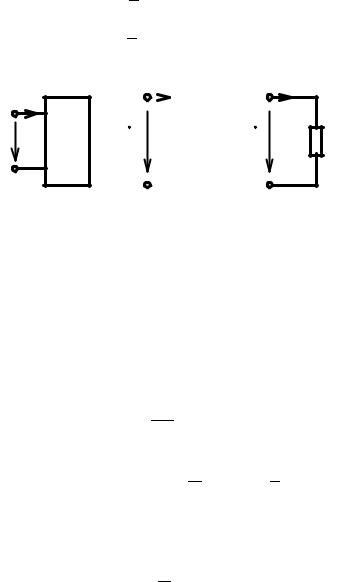
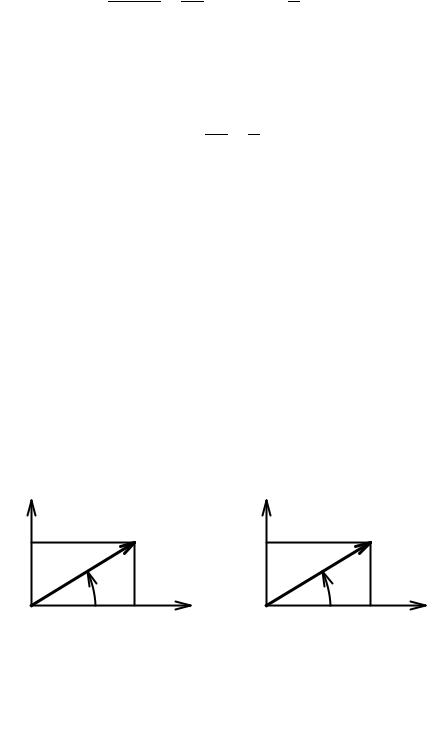
Рассмотрим произвольную линейную цепь с сосредоточенными параметрами, находящуюся под гармоническим воздействием. Выделим участок этой цепи, имею щий два внешних зажима и не содержащий источников энергии (рис. 2.7, а). Ток i и напряжение u на зажимах этого участка являются гармоническими функциями вре мени:

Рис. 2.7. Идеализированный пассивный двухполюсник (а) и его комплексные схемы заме щения (б, в)

По определению, комплексным входным сопротивлением (комплексным со­ противлением) Z пассивного участка цепи называется отношение комплексной ам плитуды напряжения на зажимах участка цепи к комплексной амплитуде тока:

. 2.42

Выражая комплексные амплитуды напряжения и тока через соответствующие комплексные действующие значения √2 ; √2 , устанавливаем, что ком плексное сопротивление пассивного участка цепи может быть также найдено как отношение комплексных действующих значений напряжения и тока:

. 2.43

Комплексное входное сопротивление пассивного участка цепи представляет собой в общем случае комплексное число; поэтому оно может быть представлено в показательной

2.44

106

и алгебраической формах.

2.45

Величины z = |Z| и φ называются соответственно модулем и аргументом ком плексного сопротивления, величины r и х его вещественной (резистивной) и мни мой (реактивной) составляющими (модуль комплексного входного сопротивления цепи z называют также полным входным сопротивлением). Представляя ком плексные амплитуды и комплексные действующие значения напряжений и токов в показательной форме, из (2.42) и (2.43) находим

. 2.46

Сравнивая (2.44) и (2.46), устанавливаем, что модуль комплексного сопротив ления z равен отношению амплитуд или действующих значений напряжения и тока на зажимах рассматриваемого участка цепи:

а аргумент равен разности начальных фаз напряжения и тока:

. 2.48

Взависимости от фазовых соотношений между напряжением и током значение

φможет быть больше нуля (напряжение опережает ток по фазе), меньше нуля (на пряжение отстает по фазе от тока) или равно нулю (ток и напряжение совпадают по фазе).

Комплексное входное сопротивление может быть представлено в виде вектора, расположенного в комплексной плоскости, длина которого в определенном масшта бе равна z, а угол наклона к положительной вещественной полуоси равен φ (рис. 2.8, а). Вещественная r и мнимая х составляющие входного сопротивления Z представ ляют собой проекции вектора Z на вещественную и мнимую оси:

Рис. 2.8. Изображение Z и Y на комплексной плоскости

107

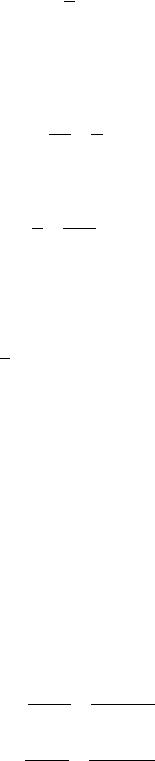
Величина, обратная комплексному входному сопротивлению, называется ком­ плексной входной проводимостью (комплексной проводимостью) участка цепи:

1 . 2.49

Комплексная входная проводимость может быть определена как отношение комплексных амплитуд или комплексных действующих значений тока и напряже ния на зажимах рассматриваемого участка цепи:

. 2.50

Представляя комплексную проводимость Y в показательной форме

1

, 2.51

находим, что модуль комплексной входной проводимости y = |Y|, называемый пол­ ной входной проводимостью цепи, является величиной, обратной модулю ком плексного входного сопротивления:

Подставляя в (2.49) Z = r + jx и Y = g + jb, определим связь между вещественными и мнимыми составляющими комплексного сопротивления и комплексной проводи мости участка цепи:

1

; 2.52

1

. 2.53

Из выражений (2.52), (2.53) следует, что резистивные составляющие комплекс ного входного сопротивления и комплексной) входной проводимости имеют одина ковые знаки:

108

комплексным сопротивлением или проводимостью, а токи и напряжения на его за жимах — комплексными амплитудами (см. рис. 2.7, б) или комплексными дейст вующими значениями (см. рис. 2.7, в).

Представляя все входящие в моделирующую цепь идеализированные пассив ные элементы их комплексными схемами замещения, а токи и ЭДС идеализирован ных источников — их комплексными амплитудами или комплексными действую щими значениями, получаем комплексную схему замещения цепи (схему замещения для комплексных амплитуд или схему замещения для комплексных действующих значений). В отличие от комплексных схем замещения, рассмотренные ранее схемы, на которых были изображены идеализированные двухполюсные элементы и указа ны мгновенные значения токов i и напряжений u ветвей и идеализированных ис точников, будем называть схемами замещения для мгновенных значений.

Таким образом, комплексная схема замещения цепи может быть получена из схемы замещения для мгновенных значений путем замены всех идеализи­ рованных пассивных двухполюсников их комплексными сопротивлениями (проводимостями) и всех токов и напряжений — их комплексными изображе­ ниями.

По внешнему виду комплексная схема замещения цепи подобна цепи постоян ного тока, составленной только из сопротивлений и идеализированных источников энергии, причем, подобно цепи постоянного тока, компонентные уравнения всех ветвей в комплексной форме являются алгебраическими.

Мгновенные значения токов и напряжений различных ветвей электрической цепи связаны между собой линейными алгебраическими уравнениями баланса то ков и напряжений, составляемыми на основании законов Кирхгофа. Учитывая, что суммированию гармонических функций времени соответствует суммирование их комплексных изображений, перейдем от законов Кирхгофа для мгновенных значе ний токов и напряжений к законам Кирхгофа для комплексных изображений токов и напряжений, называемых обычно законами Кирхгофа в комплексной форме.

Первый закон Кирхгофа в комплексной форме устанавливает связь между ком плексными изображениями токов в каждом из узлов моделирующей цепи: сумма комплексных амплитуд (комплексных действующих значений) токов всех ветвей, подключенных к каждому из узлов электрической цепи, равна нулю:

где k — номер ветви, подключенной к рассматриваемому узлу.

Второй закон Кирхгофа в комплексной форме определяет связь между ком плексными изображениями напряжений ветвей, входящих в произвольный контур электрической цепи: сумма комплексных амплитуд (комплексных действующих зна­

110

чений) напряжений всех ветвей, входящих в любой контур моделирующей цепи, равна нулю:

где — номер ветви, входящей в рассматриваемый контур.

В ряде случаев бывает удобно использовать другую формулировку второго за кона Кирхгофа в комплексной форме: сумма комплексных изображений напряжений на всех элементах любого контура моделирующей цепи, кроме источников напряже­ ния, равна сумме комплексных изображений ЭДС всех входящих в контур источников напряжения:

где , — комплексные изображения напряжений всех элементов контура, за исключением источников напряжения; , — комплексные изображения ЭДС источников напряжения, действующих в рассматриваемом контуре.

В связи с тем, что выражения (2.58) — (2.60) непосредственно вытекают из со отношений (1.39) — (1.41), при суммировании комплексных изображений токов и напряжений ветвей электрической цепи, в выражениях (2.58) — (2.60) сохраняются те же правила знаков, что и при суммировании мгновенных значений токов и на пряжений.

Законы Кирхгофа были сформулированы только для мгновенных значе­ ний, комплексных амплитуд и комплексных действующих значений токов и напряжений. Они не выполняются для амплитуд и действующих значений со­ ответствующих величин.

Используя выражения для законов Ома и Кирхгофа в комплексной форме, мож но составить систему уравнений электрического равновесия цепи для комплексных изображений токов и напряжений. В отличие от уравнений электрического равно весия, составленных для мгновенных значений токов и напряжений, уравнения электрического равновесия для комплексных изображений токов и напряжений яв­ ляются алгебраическими. Решение таких уравнений намного проще, чем решение дифференциальных уравнений электрического равновесия, составленных для мгно венных значений токов и напряжений. Таким образом, с использованием комплекс ных схем замещения и полученных на их основании уравнений электрического рав новесия цепи в комплексной форме анализ цепи переменного тока становится не сложнее анализа цепи постоянного тока и может производиться с помощью тех же приемов.

111