
- •Краткое содержание
- •Полный список примеров, задач и кейсов
- •Предисловие
- •Благодарности
- •Оптимизация в условиях полной определенности
- •1. Метод линейной оптимизации
- •Теоретические замечания.
- •Приемы решения задач
- •1.П-1. Фирма «Фасад»
- •Решение задачи.
- •1.П-2. Компания “Черные каски”
- •Решение задачи.
- •1.П-3. Сталепрокатный завод
- •Решение задачи.
- •1.П-4. На кондитерской фабрике. (Кейс)
- •Анализ Действия 1-го.
- •Действие 2-е. Жаль…, ведь мы все так любим «Батончик»!
- •Анализ Действия 2-го.
- •Дейчтвие 3-е. Проблема учета постоянных издержек
- •Анализ Действия 3-его.
- •1.П-5. Оптимизация производства на заводе «Прогресс» (Кейс)
- •Действие 1-е. Оптимальный план.
- •Первый шаг анализа
- •Второй шаг анализа (Предложение добросовестного рабочего)
- •Четвертый шаг анализа
- •Пятый шаг анализа
- •Анализ Действия 1-го.
- •1.П-6. Аренда с предоплатой
- •Решение задачи.
- •1.П-7. Большой портфель
- •Решение задачи.
- •Задачи для самостоятельного решения
- •1.1. Планирование производства
- •1.1. Три магнитофона
- •1.2. Ферма
- •1.3. Мебельная фабрика
- •1.4. Смешивание соков
- •1.5. Пять типов продукции
- •1.6. Корпорация «Тополь»
- •1.8. Выпуск процессоров
- •1.9. Предприятие в Энске
- •1.10. Электронные переключатели
- •1.11. Фермер Билл Петрушкин
- •1.13. Предприятие «Высокий октан»
- •1.14. Корпорация «Ветер»
- •1.15. Компания «Подмосковная электроника»
- •1.16. Компания «Пауэр Кулинг»
- •1.17. Добыча руды в компании “Седьмой круг”
- •1.18. Детские велосипеды
- •1.19. Горнопромышленная компания “Белые каски”
- •1.20. Предприятие Танти Мару
- •1.21. Очистка нефти
- •1.23. План ремонта станков
- •1.25. Бакалейная лавка
- •1.26. Сухофрукты
- •1.27. Джинсовая одежда
- •1.28. Сэндвичи Жаннет
- •1.29. Компания «Корвет»
- •1.30. Фильм! Фильм! Фильм!!!
- •1.31. Предприятие «Маяк»
- •1.32. Англия, Франция и Испания
- •1.2. Планы закупок
- •1.33. Том, Дик и Джерри
- •1.35. Универсальный магазин
- •1.36. Торговая фирма «Одежда не для всех»
- •1.37. Торговая фирма «Одежда для всех»
- •1.38. Оптовая торговля замороженными овощами
- •1.3. Реклама и маркетинг
- •1.40. Рекламная компания
- •1.41. Эластичность спроса
- •1.42. Фирма «JL»
- •1.43. Корпорация «Фарма Лаб» (бизнес-кейс)
- •1.45. Индекс цен на молочные продукты
- •1.4. Оптимальный состав
- •1.46. Собачья еда
- •1.47. Свиноферма
- •1.48. Фармацевтическая компания
- •1.49. Пять предприятий
- •1.51. Школьные обеды
- •1.5. Финансы
- •1.53. Банк и 6 проектов
- •1.54. Комитет планирования
- •1.55. Инвестиционный бюджет
- •1.56. Консервативный инвестор
- •1.57. Портфель инвестиций
- •1.58. Дистрибьюторская компьютерная фирма
- •1.59. Инвестор и 5 проектов
- •1.60. Частный инвестор
- •1.61. Сара Вильямс
- •1.62. Оценка прибыльности цеха бухгалтерией
- •1.63. Аренда с ежемесячными выплатами
- •1.64. Сертификаты
- •1.65. Компания «СуперИнвест»
- •1.66. Планирование финансового потока
- •1.6. Расписания и графики выполнения заказов на производстве
- •Приемы решения задач
- •1.П-8. Банк «Простор»
- •Решение задачи.
- •1.П-9. Последовательность выполнения заказов
- •Решение задачи.
- •Задачи для самостоятельного решения
- •1.68. “Ясный перец”
- •1.71. Электроэнергия
- •1.72. Последовательность обработки деталей на двух станках
- •1.73. Последовательность обработки деталей на трех станках
- •2. Транспортные задачи и логистика; задачи о назначениях и отборе.
- •Теоретические замечания.
- •Транспортная задача
- •Несбалансированность в транспортной задаче
- •Задача о назначениях
- •Задачи оптимизации логистики и цепочек поставок.
- •Приемы решения задач
- •2.П-1. Дорстрой
- •Решение задачи.
- •2.П-2. Поставки двух видов продуктов
- •Решение задачи.
- •2.П-3. Компью-Нет
- •Решение задачи.
- •2.П-4. Распределение аудиторов по фирмам
- •Решение задачи.
- •2.П-5. Заводы ЖБИ
- •Решение задачи.
- •2.П-6. Две бригады
- •Решение задачи.
- •2.П-7. Отделочный камень для коттеджей (Кейс)
- •Анализ кейса.
- •2.П-8. Цепочка поставок компании «НАЦПРОДУКТ» (Кейс)
- •Действие 1-е: Постановка задач оптимизации.
- •Анализ действия 1 кейса.
- •Определение оптимального плана закупок
- •Определение оптимального плана перевозок
- •Действие 2-е: Оптимизация и здравый смысл.
- •Анализ действия 2 кейса.
- •Действие 3-e: Интегрированный план для цепочки поставок
- •Анализ действия 3 кейса.
- •2.П-9. Фирма «Хороший хозяин»
- •Решение задачи.
- •Задачи для самостоятельного решения
- •2.1. Логистика
- •2.1. Транспортный отдел
- •2.2. Транспортные издержки
- •2.3. Поставки со складов
- •2.4. Дефицит товара
- •2.5. Дорожное строительство
- •2.6. Подготовка к отопительному сезону
- •2.7. Перевозка контейнеров
- •2.9. Поставки
- •2.10. Ремонт автодорог
- •2.11. Слишком много поставщиков
- •2.12. Производственные площадки компании «Воздух»
- •2.13. Перевозки двух продуктов
- •2.14. Перевозки трех продуктов
- •2.15. Многопродуктовая задача
- •2.16. Транспортировка через промежуточные склады
- •2.17. Два завода
- •2.18. Грузовой самолет
- •2.22. Школьные перевозки
- •2.23. Два груза разных объемов
- •2.24. Поставки отопительного оборудования
- •2.25. Воздушные перевозки.
- •2.26. Рейс машины инкассатора
- •2.2. Оптимальные назначения и отбор
- •2.27. 7 команд
- •2.28. 8 команд с проблемой
- •2.29. 9 команд
- •2.30. Олимпийские игры
- •2.31. Назначение слесарей
- •2.32. Отбор специалистов и составление команд
- •2.33. Выбор мест для складов
- •2.34. Распределение оптовиков
- •2.35. Назначение центров снабжения
- •2.36. Склады для компании «Чистые материалы»
- •2.37. Отбор и расстановка рабочих
- •2.38. Дефицит рабочих
- •2.39. Запасная бригада
- •2.40. На стройках МТС
- •2.41. Назначение бригад ремонтников
- •2.43. Проблема мастера
- •2.44. Закупки для компании «Южный производитель»
- •3. Планирование и анализ проектов
- •Теоретические замечания.
- •Приемы решения задач.
- •3.П-1. Обеспечение заданных сроков за счет сверхурочных
- •Решение задачи.
- •3.П-2. Предел еженедельного финансирования проекта.
- •Решение задачи.
- •3.П-3. Проект Омикрон
- •Решение задачи.
- •3.П-4. Научно-просветительский центр планирования семьи в Нигерии.
- •Задачи для самостоятельного решения
- •3.1. Строительный проект
- •3.2. Новый ресторан МакЛуммокс
- •3.3. Консалтинговый проект для «Чайна ОллПродакт».
- •3.4. Срыв сроков начала работ субподрядчиком.
- •3.5. Автомобиль 007
- •3.6. Строительство торгового центра
- •3.7. Проект компании МегаШоп
- •3.9. Петров и партнеры
- •3.11. Мир женщин
- •3.12. Журнал Червонный Гудок
- •3.13. Проект корпорации «SHARON CONSTRUCTION»
- •4. Оптимальное управление запасами
- •Принятые обозначения и необходимые формулы
- •Теоретические замечания.
- •[S] – денежная единица/на один заказ.
- •Модель экономичного размера заказа
- •Основные допущения и параметры модели
- •Оптимальная частота заказа для группы товаров.
- •Модель производства оптимальной партии продукции
- •Ограничения модели экономичного размера заказа (партии продукции) и возможность их преодоления.
- •Приемы решения задач.
- •4.П-1. Выбор поставщика
- •Решение задачи.
- •4.П-2. Строительная фирма
- •Решение задачи.
- •4.П-3. Лов рыбы
- •Решение задачи.
- •Задачи для самостоятельного решения
- •4.1. Выгодное предложение
- •4.2. Гостиница
- •4.3. Чековая лента
- •4.4. Военный госпиталь
- •4.5. Закупки в компании Стоик
- •4.7. Горный автомобиль
- •4.8. Сибирские моторы
- •4.11. Совхоз Чапаевец
- •4.13. Крыша
- •4.14. Предприятие АСЗ
- •4.15. Сеть магазинов «Деловой костюм»
- •5. Комплексное и многопериодное планирование
- •Приемы решения задач.
- •5.П-1. Агрегатный план производственного отдела компании «Вал» (Кейс)
- •Анализ кейса
- •Стратегия 1: Найм и увольнение.
- •Стратегия 2: Сверхурочные и частичная занятость.
- •Стратегия 3: Использование склада.
- •Оптимальная смесь стратегий.
- •Задачи для самостоятельного решения
- •5.1. План для MemoBlink
- •5.3. Ферма Бэрримора
- •5.4. Горные лыжи
- •5.6. Компания АгроМашЗавод
- •5.7. Компания «Лем и сыновья»
- •5.8. График доставки
- •Методы принятия решений в условиях неопределенности и риска
- •Принятые обозначения и необходимые формулы
- •Теоретические замечания
- •Постановка задачи о количественной оценке риска возникновения дефицита и плате за его снижение до заданного уровня.
- •Основные характеристики случайного спроса.
- •Частотное распределение случайного спроса.
- •Нормальное распределение вероятностей.
- •Оценка риска возникновения дефицита по нормальному распределению.
- •Риск возникновения дефицита и уровень обслуживания.
- •Модель фиксированного периода между заказами.
- •Замечание о случайных вариациях времени поставки.
- •Однопериодная модель заказа.
- •Замечание об экономически обоснованном риске дефицита в модели фиксированного размера заказа.
- •Приемы решения задач
- •6.П-1. Магазин сантехники
- •Решение задачи.
- •6.П-2. Оптовые продажи хозтоваров
- •Решение задачи.
- •6.П-3. Новый Электрон
- •Решение задачи.
- •6.П-4. Свежая пресса
- •Решение задачи.
- •6.П-5. Банк «Белый Тигр»
- •Решение задачи.
- •Задачи для самостоятельного решения
- •6.1. Бесконечный горизонт планирования – фиксированный запас
- •6.1. Отель
- •6.2. Офис крупной компании
- •6.3. Сэм управляет запасами
- •6.4. Мастерская
- •6.5. Стадион
- •6.6. “Биг-лайн”
- •6.7. Женский роман
- •6.8. Магазин «Кандела»
- •6.9. Местная станция обслуживания
- •6.10. Грубый Готлиб
- •6.11. Чехлы
- •6.12. Автосервис
- •6.13. Торговля пиломатериалами
- •6.14. Магазин сантехники
- •6.15. Выбор стратегии
- •6.16. Закупка сырья
- •6.17. Магазин «Хозтовары»
- •6.18. Сигнализация
- •6.19. Кухонные гарнитуры
- •6.20. Фармацевтическая компания
- •6.21. Батарейки
- •6.22. Магазин инструментов
- •6.23. Автомобильная секция
- •6.24. Системы водоснабжения
- •6.2. Бесконечный горизонт планирования – фиксированный период
- •6.26. «Пицца-Хат»
- •6.27. Универсальный магазин
- •6.28. Магазин «Свет»
- •6.29. Гамма Гидры
- •6.30. Универмаг «Приреченский»
- •6.31. Секция универсального магазина
- •6.32. Криминальное чтиво
- •6.33. Мини-Маркет
- •6.3. Однопериодная модель
- •6.35. Футболки
- •6.37. Мясной отдел
- •6.38. Компания «Маски»
- •6.40. Киоск
- •6.41. Расторопный Дмитрий
- •6.42. Бронирование контейнеров
- •6.43. Супермаркет и компания «Хозяюшка»
- •6.44. Отделение банка
- •6.45. Университет
- •6.46. Финансирование проекта
- •7. Выбор альтернатив.
- •Основные формулы теории вероятностей
- •Теоретические замечания.
- •Таблица выигрышей и потерь.
- •Принятие решений в условиях полной неопределенности
- •Принятие решений в условиях риска.
- •Стоимость совершенной информации.
- •Анализ устойчивости выбора оптимальной альтернативы для компании «Энергия палеолита».
- •Дерево альтернатив
- •Анализ устойчивости выбора оптимальной альтернативы по дереву альтернатив для компании «Вольный полет».
- •Переоценка вероятностей сценариев будущего в свете дополнительной информации. Стоимость несовершенной информации.
- •Приемы решения задач
- •7.П-1. Производитель снегоходов
- •Решение задачи.
- •7.П-2. Дефектные комплектующие
- •Решение задачи.
- •Задачи для самостоятельного решения
- •Простые сценарии развития событий
- •7.1. Производитель аэросаней
- •7.2. Оптовый склад хозяйственных товаров
- •7.3. Электротермометры
- •7.4. Хоз-маркет
- •7.5. Обувной отдел
- •7.6. Зеленщица
- •7.7. Маленькая кондитерская
- •7.8. Тракторы и СХ Орудия Барни
- •7.9. Переменный спрос
- •7.10. Супермаски
- •7.11. Компьютерная школа
- •7.12. Оптовая база
- •7.13. Елки-палки
- •7.14. Подготовка к зиме
- •7.15. Центр Компьютерного Тренинга
- •7.16. Производственная линия
- •7.17. Кредит
- •7.18. Две стратегии
- •7.19. Новый магазин
- •7.20. Турфирма «Улет»
- •7.21. Курортное местечко
- •Анализ цепочек событий
- •7.24. Парфюмерная компания
- •7.25. Производство ЭЛТ
- •7.27. Биохимическая лаборатория
- •7.30. Компания "Обуем всех"
- •7.31. Консалтинговая служба
- •7.32. Семейная инвестиционная проблема (бизнес-кейс)
- •7.33. Пекарня
- •7.34. Новый бизнес
- •7.36. Ипотечный фонд
- •7.37. Дворец-строй
- •7.38. Большая нефть
- •7.39. ОбувьСити
- •7.40. Золотой рудник
- •7.41. Риэлторская фирма г. Сидорова
- •8. Управление проектами с учетом случайных вариаций времени выполнения стадий
- •Теоретические замечания.
- •Приемы решения задач.
- •8.П-1. Проект «Снеси-Построй»
- •Задачи для самостоятельного решения
- •8.1. Простой проект
- •8.2. Проект рекрутинговой компании
- •8.3. Полная релаксация
- •9. Оценка эффективности систем массового обслуживания и их оптимизация
- •Теоретическое введение.
- •Коммунальные платежи в отделении сбербанка.
- •Пуассоновский поток заявок.
- •Усредненные характеристики работы системы массового обслуживания.
- •Классификация систем массового обслуживания
- •Расчеты характеристик СМО с помощью теории очередей.
- •Приемы решения задач.
- •9.П-1. Банкоматы
- •Решение задачи.
- •9.П-2. Кафе в парке отдыха
- •Решение задачи.
- •9.П-3. Такси по телефону
- •Решение задачи.
- •Задачи для самостоятельного решения
- •9.1. Телефонная система заказа билетов
- •9.2. Таможенный пункт
- •9.3. Большой цех
- •9.4. Приемная
- •9.5. Ресторан «Ешь вволю»
- •9.6. Торговля по каталогам
- •9.7. Таможенный досмотр
- •9.8. Бармен
- •9.9. Стоматологическая поликлиника (бизнес-кейс)
- •9.10. Парикмахерская
- •9.11. Бери и кати
- •9.12. Трасса Е95
- •9.13. Лодочная станция
- •9.14. Погрузка кирпича.
- •9.15. Бар «Аэродром»
- •9.16. Парк аттракционов
- •9.17. Офис
- •9.18. Аттракционы в парке отдыха
- •9.19. Колониальные товары
- •9.20. Мир цветов
- •9.21. Магазин сети «Шамбала»
- •9.22. Кафе «Золотая форель»
- •9.23. Серфинг
- •9.24. Радио-такси
- •9.26. Станки-автоматы
- •9.27. Полиграфическая компания
- •9.28. Кофе для преподавателя
- •9.29. Прядильная мастерская
- •9.30. Тамагочи
- •9.32. Полный порядок
- •9.33. Виртуальный друг
- •9.34. Завод научного приборостроения
- •9.35. Вязальные станки
- •Ответы к задачам
- •Оптимизация в условиях полной определенности
- •Метод линейной оптимизации.
- •1.2 Ферма
- •1.3 Мебельная фабрика
- •1.4 Смешивание соков
- •1.5 Пять типов продукции
- •1.6 Корпорация «Тополь»
- •1.9 Предприятие в Энске.
- •1.11 Фермер Билл Петрушкин
- •1.13 Предприятие «Высокий октан»
- •1.14 Корпорация «Ветер»
- •1.15 Компания «Подмосковная электроника»
- •1.16 Компания «Подмосковная электроника»
- •1.17 Добыча руды в компании “Седьмой круг”
- •1.18 Детские велосипеды
- •1.19 Горнопромышленная компания “Белые каски”
- •1.20 Предприятие Танти Мару
- •1.21 Очистка нефти
- •1.22 Производство минеральных плит
- •1.23 План ремонта станков
- •1.25 Бакалейная лавка
- •1.26 Сухофрукты
- •1.27 Джинсовая одежда
- •1.28 Сэндвичи Жаннет
- •1.29 Компания «Корвет»
- •1.30 Фильм! Фильм! Фильм!!!
- •1.31 Предприятие «Маяк»
- •1.32 Англия, Франция и Испания
- •1.33 Том, Дик и Джерри
- •1.34 Поставки химического сырья
- •1.36 Торговая фирма «Одежда не для всех»
- •1.38 Оптовая торговля замороженными овощами
- •1.39 Корпорация «Природный газ»
- •1.40 Рекламная компания
- •1.41 Эластичность спроса
- •1.42 Фирма «JL»
- •1.45 Индекс цен на молочные продукты
- •1.46 Собачья еда
- •1.47 Свиноферма
- •1.48 Фармацевтическая компания
- •1.51 Школьные обеды
- •1.53 Банк и 6 проект
- •1.56 Консервативный инвестор
- •1.58 Дистрибьюторская компьютерная фирма
- •1.60 Частный инвестор
- •1.61 Сара Вильямс
- •1.62 Оценка прибыльности цеха бухгалтерией
- •1.63 Аренда с ежемесячными выплатами
- •1.64 Сертификаты
- •1.65 Компания «СуперИнвест»
- •1.67 «Дом-строй»
- •1.68 “Ясный перец”
- •1.71 Электроэнергия
- •1.72 Последовательность обработки деталей на двух станках
- •1.73 Последовательность обработки деталей на трех станках
- •Транспортные задачи и логистика; задачи о назначениях и отборе
- •2.1 Транспортный отдел
- •2.2 Транспортные издержки
- •2.3 Поставки со складов
- •2.4 Дефицит товара
- •2.5 Дорожное строительство
- •2.6 Подготовка к отопительному сезону
- •2.7 Перевозка контейнеров
- •2.9 Поставки
- •2.10 Ремонт автодорог
- •2.11 Слишком много поставщиков
- •2.12 Производственные площадки компании «Воздух»
- •2.13 Перевозки двух продуктов
- •2.14 Перевозки трех продуктов
- •2.15 Многопродуктовая задача
- •2.16 Транспортировка через промежуточные склады
- •2.17 Два завода
- •2.22 Школьные перевозки
- •2.23 Два груза разных объемов
- •2.24 Поставки отопительного оборудования
- •2.25 Воздушные перевозки.
- •2.26 Рейс машины инкассатора
- •2.27 7 команд
- •2.28 8 команд с проблемой
- •2.29 9 команд
- •2.30 Олимпийские игры
- •2.31 Назначение слесарей
- •2.32 Отбор специалистов и составление команд
- •2.33 1:1:2:7: Выбор мест для складов
- •2.34 Распределение оптовиков
- •2.35 Назначение центров снабжения
- •2.36 Склады для компании «Чистые материалы»
- •2.37 Отбор и расстановка рабочих
- •2.38 Дефицит рабочих
- •2.39 1:2:2:13. Запасная бригада
- •2.40 На стройках МТС
- •2.41 Назначение бригад ремонтников
- •2.43 Проблема мастера
- •2.44 Закупки для компании «Южный производитель»
- •Планирование и анализ проектов
- •3.1 Строительный проект
- •3.2 Новый ресторан МакЛуммокс
- •3.3 Консалтинговый проект для «Чайна ОллПродакт».
- •3.4 Срыв сроков начала работ субподрядчиком.
- •3.5 Автомобиль 007
- •3.6 Строительство торгового центра
- •3.7 Строительство торгового центра
- •3.9 Петров и партнеры
- •3.11 Мир женщин
- •3.12 Журнал Червонный Гудок
- •3.13 Проект корпорации «SHARON CONSTRUCTION»
- •Оптимальное управление запасами
- •4.2 Гостиница
- •4.3 Чековая лента
- •4.5 Закупки в компании Стоик
- •4.7 Горный автомобиль
- •4.8 Сибирские моторы
- •4.10 ЖК-панели
- •4.11 Совхоз Чапаевец
- •4.13 Крыша
- •4.14 Предприятие АСЗ
- •4.15 Сеть магазинов «Деловой костюм»
- •Комплексное и многопериодное планирование
- •5.1 План для MemoBlink
- •5.3 Ферма Бэрримора
- •5.4 Горные лыжи
- •5.5 Компания Красный молот
- •5.6 Компания АгроМашЗавод
- •5.7 Компания «Лем и сыновья»
- •5.8 График доставки
- •Методы принятия решений в условиях неопределенности и риска
- •Оптимальное управление запасами с учетом случайных вариаций спроса
- •6.1 Отель
- •6.2 Офис крупной компании
- •6.3 Сэм управляет запасами
- •6.4 Мастерская
- •6.5 Стадион
- •6.6 “Биг-лайн”
- •6.7 Женский роман
- •6.8 Магазин «Кандела»
- •6.9 Местная станция обслуживания
- •6.10 Грубый Готлиб
- •6.11 Чехлы
- •6.12 Автосервис
- •6.13 Торговля пиломатериалами
- •6.14 Магазин сантехники
- •6.15 Выбор стратегии
- •6.16 Закупка сырья
- •6.17 Магазин «Хозтовары»
- •6.18 Сигнализация
- •6.19 Кухонные гарнитуры
- •6.20 Фармацевтическая компания
- •6.21 Батарейки
- •6.22 Магазин инструментов
- •6.23 Автомобильная секция
- •6.24 Системы водоснабжения
- •6.26 «Пицца-Хат»
- •6.27 Универсальный магазин
- •6.28 Магазин «Свет»
- •6.29 Гамма Гидры
- •6.30 Универмаг «Приреченский»
- •6.31 Секция универсального магазина
- •6.32 Криминальное чтиво
- •6.33 Мини-Маркет
- •6.35 Футболки
- •6.37 Мясной отдел
- •6.38 Компания «Маски»
- •6.39 Шубы
- •6.40 Киоск
- •6.41 Расторопный Дмитрий
- •6.42 Бронирование контейнеров
- •6.43 Супермаркет и компания «Хозяюшка»
- •6.44 Отделение банка
- •6.45 Университет
- •6.46 Финансирование проекта
- •Выбор альтернатив
- •7.1 Производитель аэросаней
- •7.2 Оптовый склад хозяйственных товаров
- •7.3 Электротермометры
- •7.4 Хоз-маркет
- •7.5 Обувной отдел
- •7.6 Зеленщица
- •7.7 Маленькая кондитерская
- •7.8 Тракторы и СХ Орудия Барни
- •7.9 Переменный спрос
- •7.10 Супермаски
- •7.11 Компьютерная школа
- •7.12 Оптовая база
- •7.13 Елки-палки
- •7.14 Подготовка к зиме
- •7.15 Центр Компьютерного Тренинга
- •7.16 Производственная линия
- •7.17 Кредит
- •7.18 Две стратегии
- •7.19 Новый магазин
- •7.20 Турфирма «Улет»
- •7.21 Курортное местечко
- •7.24 Парфюмерная компания
- •7.25 Производство ЭЛТ
- •7.26 Пробка
- •7.27 Биохимическая лаборатория
- •7.28 Повышение квалификации
- •7.30 Компания "Обуем всех"
- •7.31 Консалтинговая служба
- •7.32 Семейная инвестиционная проблема
- •7.33 Пекарня
- •7.34 Новый бизнес
- •7.36 Ипотечный фонд
- •7.37 Дворец-строй
- •7.38 Большая нефть
- •7.39 ОбувьСити
- •7.40 Золотой рудник
- •7.41 Риэлторская фирма г. Сидорова
- •7.42 Покупка магазина
- •Управление проектами с учетом случайных вариаций времени выполнения стадий
- •8.1 Простой проект
- •8.2 Проект рекрутинговой компании
- •8.3 Полная релаксация
- •Оценка эффективности систем массового обслуживания и их оптимизация
- •9.1 Телефонная система заказа билетов
- •9.2 Таможенный пункт
- •9.3 Большой цех
- •9.4 Приемная
- •9.5 Ресторан «Ешь вволю»
- •9.6 Торговля по каталогам
- •9.7 Таможенный досмотр
- •9.8 Бармен
- •9.9 Стоматологическая поликлиника
- •9.10 Парикмахерская
- •9.11 Бери и кати
- •9.12 Трасса Е95
- •9.13 Лодочная станция
- •9.14 Погрузка кирпича.
- •9.15 Бар «Аэродром»
- •9.16 Парк аттракционов
- •9.17 Офис
- •9.18 Аттракционы в парке отдыха
- •9.19 Колониальные товары
- •9.20 Мир цветов
- •9.21 Магазин сети «Шамбала»
- •9.22 Кафе «Золотая форель»
- •9.23 Серфинг
- •9.24 Радио-такси
- •9.26 Станки-автоматы
- •9.27 Полиграфическая компания
- •9.28 Кофе для преподавателя
- •9.29 Прядильная мастерская
- •9.30 Тамагочи
- •9.32 Полный порядок
- •9.33 Виртуальный друг
- •9.34 Завод научного приборостроения
- •9.35 Вязальные станки
- •Глоссарий
2,2 |
|
|
|
|
|
|
|
|
|
|
2,0 |
|
|
|
|
|
|
|
|
|
|
1,8 |
|
|
|
|
|
|
|
|
|
|
1,6 |
|
|
|
|
|
|
|
|
|
|
1,4 |
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
Рис. 200 |
|
|
|
|
|
|
|
|
|
|
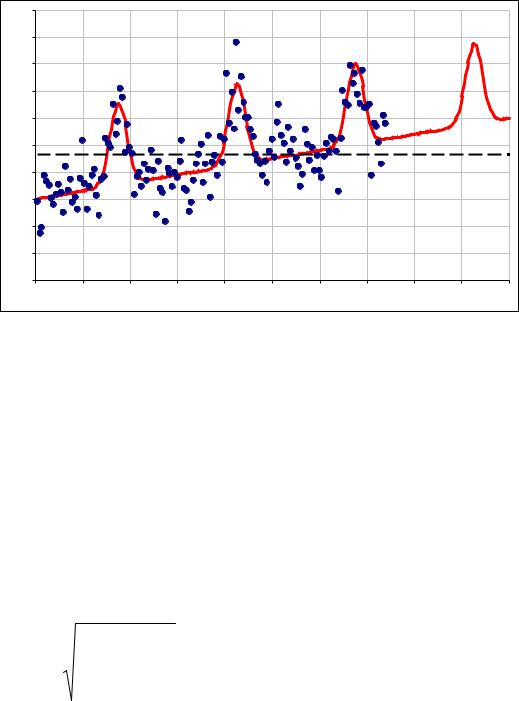
Разумеется, невозможно определить, как долго обнаруженная тенденция |
||||||||||
будет продолжаться. Однако если она существовала достаточно долго в прошлом, |
||||||||||
есть основания надеяться, что она сохранится и в ближайшем будущем. |
|
|||||||||
Полученная линия тренда определяет ожидаемое (среднее) значение |
||||||||||
спроса в разные моменты времени в прошлом и в будущем |
x(t) . Кроме того, |
|||||||||
применяемый статистический метод прогноза обязательно выдаст стандартное |
||||||||||
отклонение точек выборки от линии тренда –s (поскольку сама линия проведена |
||||||||||
на основе минимизации s2). |
|
|
|
|
|
|
|
|
||
Подчеркнем, что если все же вычислить ожидаемый спрос, как простое |
||||||||||
среднее, получится линия «прогноза», показанная пунктиром на Рис. 200. |
||||||||||
Предсказываемое этой линией «ожидаемое» значение спроса не может иметь |
||||||||||
ничего общего с действительностью, но, что еще более важно, вычисленное на |
||||||||||
основе этого «ожидаемого» значения стандартное отклонение спроса |
|
|
||||||||
N
(xi x)2
s |
i 1 |
|
N 1 |
||
|
будет, очевидно, намного больше реального.
Частотное распределение случайного спроса.
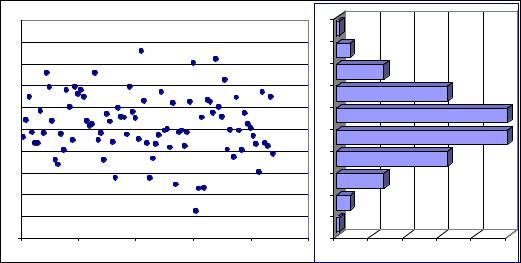
Разобьем весь диапазон изменения спроса (в нашей выборке спрос заключен в пределах от 0 до 2-х контейнеров) на небольшое число более мелких интервалов так, чтобы в каждый из них попали какие-то точки из нашей выборки (Рис. 201 а). Подсчитаем количество точек выборки , попавших в каждый такой интервал и построим диаграмму частотного распределения спроса (Рис. 201 б).
Зайцев М.Г., Варюхин С.Е. |
401 |
Площадь каждого из прямоугольников на этой диаграмме равна доли точек, попадающих в интервал, на который такой прямоугольник опирается (Рис. 201 б). Очевидно, что сумма площадей всех прямоугольников на диаграмме частотного распределения равна 1.
2.0 |
|
|
|
|
|
1.9 |
|
|
b) |
|
|
1.8 |
a) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1.7 |
|
|
|
|
|
|
1.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
1.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3 |
|
|
|
|
|
|
1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.1 |
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0% |
5% |
10% |
15% |
20% |
25% |
|
0 |
20 |
40 |
60 |
80 |
100 |
Рис. 201
Частотное распределение дает оценку вероятности попадания спроса в каждый из выделенных интервалов. С его помощью можно попытаться оценить риск дефицита. Представим себе, что мы планируем запас товара на один день, зная, что средний спрос равен 1 контейнеру. Допустим, что мы собираемся оставить на один день торговли 1,2 контейнера данного товара. Какова будет вероятность того, что спрос превысит наш запас, и возникнет дефицит?
Для ответа на этот вопрос попробуем просто сложить площади прямоугольников, опирающихся на интервалы [1,2-1,4], [1,4-1,6], [1,6-1,8] и [1,8- 2,0] (Рис. 201 б). Площадь каждого из прямоугольников равна частоте, с которой спрос из нашей выборки попадал в каждый из этих интервалов. Сумма площадей этих прямоугольников, очевидно, покажет, как часто спрос превышал 1,2 контейнера. В данном случае окажется, что это частота равна 0,22 (22 точки из 100 вошедших в выборку лежат выше ординаты 1,2).
Если эту частоту, которая относится к случайной выборке из истории продаж данного товара использовать, как оценку вероятности того, что спрос превысит 1,2 контейнера, то получается, что вопрос об оценки риска возникновения дефицита решен.
Однако, на самом деле, оценка вероятности по частоте всегда сопряжена с ошибкой, которая тем больше, чем меньше размер выборки. Если мы подбрасываем монету 10 раз, то вполне возможно, что орел выпадет 8 раз, что приведет к оценке выпадения монетки на орла равной 0,8. Разумеется, если подбросить монету 100 раз, выпадение орла 80 раз практически исключено, и оценка вероятности получится гораздо более близкой к 0,5.
Статистика позволяет оценить ошибки в оценках вероятности по частоте и среднего и стандартного отклонения по выборке (см. для справки здесь и далее,
например, книгу В.Н. Сулицкий, Методы статистического анализа в управлении, «Дело», Москва, 2002). Допустим, в нашем случае выборки из 100 чисел – значений спроса на некоторый товар за предшествующие 100 дней, среднее

значение оценено как x 1, а стандартное отклонение спроса - как s 0,1. Тогда стандартная ошибка x в определении среднего составит
x |
s |
1% , |
(9) |
|
N |
||||
|
|
|
где N=100 – размер выборки. Такого же порядка будет и ошибка в определении стандартного отклонения s (хотя формула для нее будет сложнее). А
вот относительная стандартная ошибка в определении вероятности p попадания случайного спроса в тот или иной интервал частотной диаграммы будет равна
p |
|
(1 p) |
, |
(10) |
p |
pN |
что для p 0,1 и N = 100 составит величину в 30%, а для p 0,01 – почти 100%! Разумеется, увеличение размера выборки позволяет уменьшить и ошибки в оценке распределения вероятностей, однако, на практике в бизнесе редко удается получить большие выборки. Кроме того, если, как в случае, показанном на Рис. 200, среднее (ожидаемое) значение спроса меняется со временем, получение адекватного частотного распределения существенно усложняется.
Вместе с тем, оказывается, что во многих случаях специальных исследований для оценки распределения вероятностей интересующей нас величины (в частности, распределения вероятностей различных значений спроса) по частотному распределению выборочных значений не требуется. Дело в том,
что если нас интересует суммарный спрос за несколько (L) дней или суммарный спрос в нескольких сравнимых друг с другом торговых точек, то его распределение заранее известно.
Независимо от того, как распределено каждое случайное слагаемое в сумме случайных величин, сама сумма должна быть распределена нормально со средним значением, равным сумме средних значений слагаемых (формула 4) и дисперсией, равной сумме дисперсий слагаемых (формула 5).
Это утверждение выражает важнейший статистический закон, известный как центральная предельная теорема теории вероятностей [5,8]. Везде, где мы имеем дело с суммой случайных величин (не важно, одинаково распределенных или нет, если только одна или несколько из них не доминируют над всеми остальными), мы встречаем это замечательное распределение вероятностей. Даже если речь идет о спросе за 1 день, он весьма часто формируется благодаря множеству малых случайных факторов, и потому также распределен нормально. Это распределение очень часто встречается на практике и в других случаях (именно поэтому оно и называется нормальным). Вследствие этого стоит изучить его свойства и использовать для оценки различных рисков, в частности, риска возникновения дефицита.
Нормальное распределение вероятностей.
Нормальное распределение для плотности вероятности случайной величины имеет вид:

Зайцев М.Г., Варюхин С.Е. |
|
|
|
|
|
|
403 |
||||
|
|
1 |
e |
(x x)2 |
|
|
|
|
|
|
|
p(x) |
|
2sx2 |
, |
|
|
|
|
(11) |
|||
где x |
|
2 |
|
|
|
|
|
|
|
|
|
- |
среднее значение случайной величины (например, ожидаемое |
||||||||||
значение случайного спроса), а sx – ее стандартное отклонение. |
|
||||||||||
Это распределение было введено Гауссом еще в 18 веке. Затем два |
|||||||||||
российских математика – П.Чебышев и А.Марков в конце 19 и в начале 20 века, |
|||||||||||
доказали (во все более общих предположениях) центральную предельную |
|||||||||||
теорему о том, что сумма большого числа любых слагаемых распределена в |
|||||||||||
соответствие с этим распределением, где |
x |
равно |
сумме |
средних значений |
|||||||
слагаемых (4), а дисперсия sx2 |
- равна сумме дисперсий каждого слагаемого (5). |
||||||||||
Чтобы не вдаваться в точное определение плотности распределения |
|||||||||||
вероятности, несколько упрощенно, можно представить себе, что описанная |
|||||||||||
формулой (11) кривая – это огибающая частотного распределения, составленного |
|||||||||||
из очень узких столбиков, площадь каждого из которых дает вероятность того, |
|||||||||||
что случайная величина (спрос) попадет в тот интервал, на котором столбик |
|||||||||||
построен (Рис. 202). Сумма площадей всех прямоугольников на этой диаграмме, |
|||||||||||
т.е. площадь под кривой нормального распределения равна 1. |
|
||||||||||
p(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
-3 |
|
-2 |
|
-1 |
0 |
1 z 2 |
3 |
z 4 |
|
Рис. 202 |
|
|
|
|
|
|
|
|
|
|
|
Интересно, что выбором масштаба все нормальные кривые (с разными |
|||||||||||
средними значениями и стандартными отклонениями) можно свести к одной. |
|||||||||||
Если ввести величину z, равную |
|
|
|
|
|
||||||
z x x , |
|
|
|
|
|
|
(12) |
|
|
||
sx |
|
|
|
|
|
|
|
|
|
|
|
и измеряющую величину отклонения спроса от его среднего значения, |
|||||||||||
выраженную в единицах стандартного отклонения, то получится, так называемое |
|||||||||||
