9. Оценка эффективности систем массового обслуживания и их оптимизация

Теоретическое введение.

Начнем рассмотрение вопроса об оценки пропускной способности и экономической эффективности систем массового обслуживания (СМО) с простого примера.

Коммунальные платежи в отделении сбербанка.

В отделение сбербанка для оплаты коммунальных услуг и др. счетов 9-10 числа каждого месяца заходит в среднем 28 человек в час (примем, что этот поток приблизительно постоянен в течение всего рабочего времени кассы). Опыт показывает, что оператор тратит в среднем 4 мин на человека.

Сколько Вы бы задействовали операторов (окошек), чтобы обслужить этот поток?

Как Вы оцениваете, будет ли при этом очередь? Сколько людей будет ожидать обслуживания (в среднем)?

Как Вы оцениваете, сколько примерно времени (в среднем) каждый посетитель будет проводить в сберкассе для оплаты своих счетов?

Операторы - добросовестные, не отлучаются и работают весь день с постоянной скоростью, как машины, если есть посетители. Если посетителей нет - они отдыхают (и раздражают начальство своим бездействием). Какую долю времени, Вы думаете, они будут не заняты?

Авторы многократно задавали эти вопросы в самых различных учебных группах для выявления типичных интуитивных реакций. Эти реакции, в массе своей, независимо от возраста и опыта слушателей, весьма сходны. Примерно две трети участников предлагают задействовать два окошка, полагая, что людей, ожидающих своей очереди оплатить счета, будет от 2 до 7 человек. Соответственно, предполагается, что в среднем человек, зашедший в отделение сбербанка, проведет в нем от 8 до 18 минут.

Все эти оценки выглядят весьма естественно. Действительно, если один оператор в среднем тратит на клиента 4 минуты, то за 1 час он сможет обслужить в среднем 15 клиентов. Два оператора обслужат 30 клиентов, а в среднем их заходит в отделение 28 человек в час. Таким образом, кажется, что два оператора вполне справятся с таким потоком клиентов. Нетрудно сосчитать, что в среднем каждый оператор будет иметь 4 минуты в час (или 1/15 часть часа) свободного времени, т.е. процент его загрузки составит (1-1/15)= 93%, что кажется вполне приемлемой цифрой (особенно с точки зрения плановоучетного отдела предприятия). Если в очереди находится от 2 до 7 человек (как предполагают наши респонденты), то человек, стоящий в конце очереди подойдет к окошку через время от 4 до 14 минут. Действительно, за 4 минуты 2 оператора обслужат двух человек, а 7 человек будут обслужены за 14 минут.

(Заметим, что увеличение до 29, 29.5 и 30 существенно не изменит

результаты в табл.2, так как критическим значением будет теперь 45 ( )). Так какой же вариант решения следует предпочесть в нашем простом

примере: 2 оператора или 3? Прежде чем сформулировать ответ на этот вопрос заметим, что среди ответов наших респондентов (крайне редко!) попадалось предложение задействовать только одного оператора. Такое предложение всегда встречалось аудиторией с недоумением. В ответ на это недоумение звучало что-то вроде: «Ну, а куда они (клиенты) денутся? Ведь платить-то все равно нужно. Ну и пусть постоят в очереди, или пусть приходят в другие дни». Хотя это предложение звучит не очень красиво и даже цинично, оно дает ключ к решению проблемы, сколько операторов необходимо иметь в нашей сберкассе и, более общо, какое количество каналов обслуживания необходимо иметь в той или иной системе массового обслуживания. В рыночной экономике (в отличие от социалистической) стремление к наилучшему обслуживанию клиентов продиктовано не альтруистическими («Все для блага человека!»), а экономическими соображениями. Если длинные очереди или большое время ожидания обслуживания отпугивают клиентов от покупки продукта или услуги в предприятиях вашей компании, вследствие чего уменьшается спрос и выручка от продаж, вы постараетесь оценить эти потери и уменьшить их, вводя новые каналы обслуживания. Если же ваша компания является монополистом в данной области (как в настоящее время Сбербанк в сфере коммунальных платежей), и клиентам действительно «некуда деваться», то экономических причин для увеличения числа каналов обслуживания нет. Поэтому сберкассы с одним или двумя окошками (там, где хотелось бы иметь 3-х или 4-х операторов) реально встречаются очень часто. По мере роста доходности этого вида услуг и появления конкурентов, число окошек непременно увеличится.

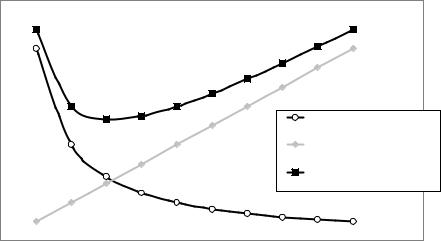
Итак следует соотносить уменьшение потерь от длинных очередей с увеличением затрат на содержание дополнительных каналов обслуживания. Качественно соотношение между этими издержками можно представить в виде графика, похожего на тот, который уже встречался при выводе оптимального размера заказа в теоретическом введении к разделу «Оптимальное управление запасами» (Рис. 292).

Издержки на содержание каналов обслуживания обычно можно считать прямо пропорциональными числу каналов, а издержки от ожидания клиентов (или сотрудников) в очереди – пропорциональными длине очереди или времени ожидания, которые, согласно формулам теории очередей, резко падают с увеличением числа каналов обслуживания. В результате можно оценить оптимальное число каналов обслуживания, минимизирующее полные издержки, связанные с функционированием системы массового обслуживания.

Издержки на содержание каналов обслуживания – это прямые расходы, которые весьма легко оценить. Издержки от ожидания в очереди клиентов (или сотрудников) – это альтернативные издержки, упущенная выгода (если, например, клиенту надоело ждать, и он ушел) и потери от утраты доброго отношения клиентов (потери от уменьшения будущих продаж). В некоторых случаях (сотрудники стоят в очереди на ксерокс, механики автосервиса ждут в очереди получения необходимой детали со склада) эти издержки могут быть легко оценены. В случае если в очереди стоят клиенты, оценка издержек от ожидания оказывается более сложной и может быть сделана лишь ориентировочно. Однако

влюбом случае сначала нужно установить связь между издержками от ожидания

вочереди с длиной очереди или временем ожидания, а затем использовать теорию очередей для оценки этих характеристик в зависимости от интенсивности входного потока, скорости обслуживания и числа каналов обслуживания.

Пуассоновский поток заявок.

Теория очередей предполагает, что входной поток клиентов (или заявок на обслуживание) описывается вероятностной моделью, которая называется

простейшим или пуассоновским потоком. Чтобы быть пуассоновским потоком, входной поток заявок должен обладать тремя свойствами. Он должен быть

ординарным,

стационарным,

без памяти.

Ординарный - это значит, что все заявки поступают в систему по одной, а

не группами. Например, если группа слушателей программы МВА в перерыв между парами устремляется в буфет, свойство ординарности потока нарушается, и правильно описать такую ситуацию теория очередей не сможет.

Свойство стационарности означает неизменность потока во времени. Требование стационарности не означает, разумеется, что в каждый час, минуту или день в систему приходит одинаковое число заявок. Теория очередей рассматривает входной поток как случайный, т.е. если взять два последовательных и равных промежутка времени, то в систему будет приходить разное (случайное) число заявок. Однако среднее число заявок, взятое по большому числу реализаций случайного процесса, в каждом равном промежутке времени будет одно и то же. Если, например, наблюдая некоторую столовую изо дня в день, мы обнаружим, что входной поток клиентов (а с ним и очередь) нарастает с момента открытие в 10 часов утра и достигает максимума в «часы пик» от 13 до 14, а затем идет на убыль, то свойство стационарности не выполняется.

Свойство отсутствие памяти означает, что вероятность поступления в систему очередной заявки в следующий час или минуту, совершенно не зависит

от того, сколько времени прошло с момента поступления предыдущей заявки. Заявки поступают в систему независимо друг от друга, и очередная заявка «не знает» (и потому «не может помнить») когда пришла предыдущая. Если вы ждете троллейбус на остановке уже 15 минут (а на табличке написано, что средний промежуток времени между ними составляет 5 минут), то, вместе со все возрастающим чувством досады, растет и вероятность того, что он все-таки придет в следующую минуту. В движении троллейбусов есть следы расписания. Хотя из-за случайных вариаций во времени обработки на предыдущих производственных этапах, детали на конвейер могут поступать в случайные моменты времени, «память» (или «следы расписания») в этом потоке, несомненно, присутствует. Применение формул теории очередей к таким процессам (по крайней мере, без всяких поправочных коэффициентов) неправомерно. А вот для потоков клиентов или заявок в системы массового обслуживания отсутствие памяти это очень характерное свойство. Неважно, когда

поступила предыдущая заявка, вероятность P того, что новая заявка поступит в

где - это интенсивность входного потока заявок, т.е. среднее число заявок, поступающих в единицу времени. Это равенство будет выполняться тем

точнее, чем меньше выбранный промежуток времени, при условии, что t<<1. Пусть P(t) – это вероятность того, что за время t в систему не поступит ни

одной заявки, а P(t+ t) – вероятность того, что и за время t+ t ни одной заявки в систему не придет. Тогда очевидно, что между двумя вероятностями существует следующая связь:

т.е. вероятность того, что заявка не поступит в систему за время t+ t есть произведение вероятностей двух независимых событий: 1) заявка не

2) заявка не поступила в систему за следующий малый промежуток времени t. Если раскрыть скобки, можно получить следующее дифференциальное уравнение:

Для читателей, знакомых с элементами дифференциального и интегрального исчисления, из (3) нетрудно получить, что выражение для

вероятности того, что за время t в систему не поступит ни одной заявки:

а вероятность того, что за время t в систему поступит хотя бы одна заявка, будет, очевидно, выражаться формулой:

Из формулы (5) следует, что частотное распределение для промежутка времени между последовательными заявками, поступившими в систему, будет экспоненциальным распределением