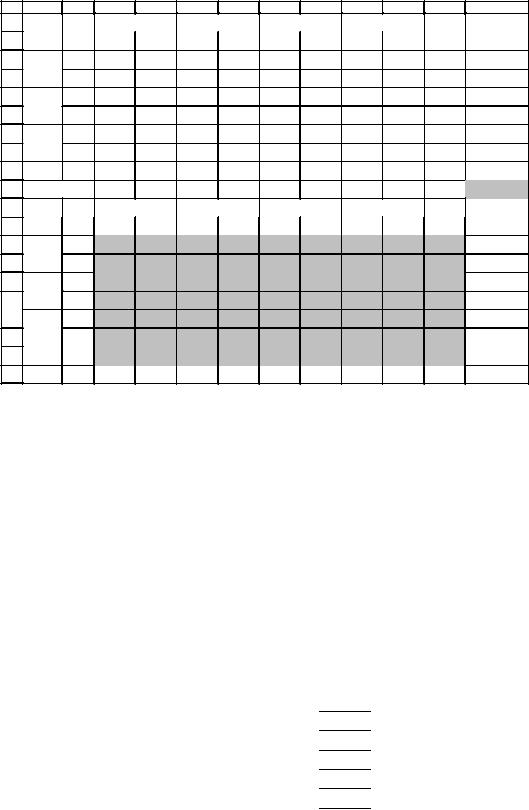
Проще всего это сделать через меню Правка\Заменить… -> Найти: 10000, Заменить на: -10000, Заменить все.

После замены запускаем Поиск решения вновь и меняем цель поиска на максимум.

Рис. 71

В полученном решении (Рис. 71) суммарная стоимость перевозок возрастает до 122930 рублей. Таким образом, наихудший план отличается от лучшего меньше чем на 20%, что дает определенную свободу выбора среди возможных планов перевозок.

2.П-3. Компью-Нет

Зам директора по персоналу фирмы «Компью-Нет» должен составить 6 пар-команд из техника-программиста и специалиста по маркетингу для работы по установке компьютерных сетей по индивидуальным требованиям клиентов. Пары составляются из вновь набранных сотрудников, среди которых проведен специальный психологический тест на взаимную совместимость. Индекс совместимости варьирует от 20 (выраженная враждебность) до 1 (возможность дружеских отношений), и для каждой потенциальной пары приведен в таблице.

a.Определите такое распределение по парам, которое обращает в минимум суммарный индекс совместимости.

b.Каков наихудший индекс совместимости у отобранных пар?

c.Определите, сколько имеется лучших, в смысле суммарного индекса, решений.

d.Можно ли так подобрать пары, чтобы ни один индекс совместимости не превышал 6?

Решение задачи.

В данном случае, учитывая что каждый из сотрудников должен быть назначен только один раз (составляются пары), задачу можно сразу определить, как задачу о назначениях. Так как количество программистов равно количеству специалистов по маркетингу (их по шесть человек), то задача сбалансирована. По условию задачи никаких запретов на составление определенных пар нет, следовательно, эта задача не содержит никаких осложнений. Поэтому прямо решаем ее по стандартной схеме.

Сначала скопируем таблицу данных и вставим ее чуть ниже по странице. Выделим в ней область данных и сотрем их – в освобожденных ячейках, в данном случае B11:G16, будут располагаться переменные задачи (Рис. 72)

Рис. 72

Так как эта задача – задача о назначениях, то переменные должны в итоге принять какое-либо из двух возможных значений: 0 или 1. Значение переменной 1 в ячейке С14, к примеру, означает, что будет создана команда из программиста Николая и специалиста по маркетингу Маши. И напротив, если в ячейке, находящейся на пересечении некоторого столбца и некоей строки, содержится 0, значит, данная команда не будет создана. При этом, если найти суммы переменных по столбцам или строкам, как это сделано в представленной таблице, то все они в правильном решении должны оказаться равными 1. Это будет означать, что каждый из программистов назначен только в одну команду, как и каждый из специалистов по маркетингу.

В таком случае, для переменных, принимающих только значения 0 и 1, в каждой строке и в каждом столбце переменных будет содержаться только одна единица, а все остальные переменные останутся нулевыми.

Далее, для построения целевой функции, нужно рассчитать суммарный индекс совместимости команд. Его можно вычислить используя всего одну хорошо известную нам формулу =СУММПРОИЗВ( ), если применить ее не для двух строк или столбцов, а для двух таблиц. Разумеется размер таблиц так же должен совпадать.

Итак, запишем в ячейку I8 формулу: =СУММПРОИЗВ(B2:G7;B11:G16). Если в нижней таблице – таблице переменных B11:G16 – будут содержаться только нули и шесть единиц, формирующих пары, результатом выполнения функции станет сумма индексов совместимости для всех шести пар. При показанном в таблице (Рис. 72) состоянии переменных результатом вычисления функции будет число 9, на которое умножится единственная единица, соответствующая паре Маша-Николай.

Вообще говоря, тут уже можно было бы поставить задачу Поиску решения. Однако заметим, что во втором вопросе идет речь об индексах совместимости для каждой пары, а этой информации мы не имеем, так как вычислили сразу сумму. Давайте вычислим индексы для каждой пары отдельно.

Если записать в ячейке I2 формулу =СУММПРОИЗВ(B2:G2;B11:G11), то мы сможем вычислить индекс пары, которую техник-программист Иван составит с кем-либо из специалистов по маркетингу. Протягивая формулу вниз, на ячейки I3:I7, мы получим такие индексы для всех остальных пар, так как в каждую пару обязательно входит один из техников-программистов.

Безусловно, можно было бы вычислять индексы и для пар, составляемых специалистами по маркетингу с кем-либо из программистов. Для этого в строке B9 нужно было ввести формулу =СУММПРОИЗВ(B11:B16;B2:B7), и протянуть ее вправо. Результат, в смысле составляемых пар, в обоих случаях один и тот же.

Теперь все готово для решения задачи. Вызываем Поиск решения и указываем целевую ячейку – I8. Так как чем меньше индекс, тем лучше, в качестве цели указываем поиск минимума. Переменные задачи B11:G16. В параметрах обязательно указываем, что подразумевается линейная модель и что переменные неотрицательны. Ограничений в задаче о назначениях, как и в транспортных задачах, должно быть всего 2 (групповых). Ограничение H11:H16=H2:H7 требует, чтобы каждый из техников-программистов был назначен только один раз (столбец H2:H7 содержит только единицы), а ограничение B17:G17=B8:G8 требует того же для специалистов по маркетингу.

Замечание: В ограничениях можно было бы написать и H11:H16=1 и B17:G17=1, однако это было бы не в духе идеологии Excel. Первый способ является более гибким для модификации и исследования исходной задачи. В прочих задачах вы в этом убедитесь. Кроме этого, в такой форме записи ограничений задача о назначениях полностью совпадает с транспортной, что позволяет использовать для решения нескольких разных задач один и тот же однажды сделанный шаблон.

Хотя мы ожидаем получить в качестве решения задачи двоичные значения переменных, нет необходимости вводить это в качестве дополнительного ограничения задачи. Напоминаем, что для решения транспортных задач, используется особый алгоритм в Поиске решения, при котором переменные автоматически остаются целыми. Этот алгоритм очень быстр, он может быть в тысячи раз быстрее алгоритма «ветвей и границ», с

помощью которого решаются линейные задачи с целочисленными переменными. И хотя на простых задачах с малым числом переменных этого можно и не заметить, но для реальных задач разница будет весьма существенной.

Результатом решения будет следующая таблица (Рис. 73). Суммарный индекс совместимости равен 19. Таблица переменных дает распределение по парам: Иван-Аня, Михаил-Маша, Павел-Лиза, Николай-Ольга, Алексей-Софья и Петр-Катя.

Рис. 73

Вполученном решении индексы совместимости пар принимают значения от 1 до 8, где 8 и есть наихудший индекс среди всех пар. Следует отметить, что и он ниже границы безразличия (10).

При решении задачи мы молчаливо предполагали, что решение будет единственным, но, вообще говоря, это далеко не всегда так. Вполне вероятно, что таблица совместимостей допускает несколько разбиений по парам, дающих одинаковый результат в смысле суммарного индекса. Может оказаться, что для наилучшего суммарного индекса так же имеется несколько возможных составов пар.

Ксожалению, надстройка Поиск решения не имеет какого-либо механизма, позволяющего получить все такие решения. Можно, однако, получив одно решение, запустить Поиск решения еще раз, не обнуляя переменные. В случае, если есть и другие решения, новое решение будет получено. Несколько раз запуская Поиск решения и сохраняя полученный результат вы можете получить набор вариантов разбиения, имеющих различные индексы пар, но одинаковый суммарный индекс.

Вэтой задаче вы можете получить два разных разбиения по парам, одно показано выше, а второе имеет следующий набор индексов пар: 4, 4, 1, 1, 8, 1.

Ксожалению, возможность получить несколько решений, из-за каких-то особенностей надстройки Поиск решения, зависит от неизвестных нам параметров настройки компьютера, на котором делается расчет. В некоторых случаях удается получить только одно решение и попытки пересчета ни к чему не

приводят. Если есть возможность, попробуйте сделать расчеты на разных компьютерах.

Чтобы вернуться к исходному решению следует стереть все переменные и повторить расчет.

Итак, имеется 2 решения задачи с суммарным индексом совместимости 19. Так как в обоих решениях самый плохой индекс 8, то ни одно из них не имеет какого-либо преимущества.

Ответ на последний вопрос (d) не представляет особенных проблем, в смысле организации задачи. Но зато поднимает целый пласт интересных вопросов, часть из которых мы сейчас обсудим.

Как мы увидели при поиске оптимального решения, во всех альтернативных планах решения лучше, чем с максимальным индексом 8, нет. Но значит ли это, что вообще плана с индексами не хуже 6 не существует? Разумеется, нет.

Вполне могут существовать множество планов с индексами не хуже 6, но зато с суммарным индексом выше 19! Поиск решения, естественно, игнорирует эти планы, потому что ищет план с наименьшим суммарным индексом. Но мы готовы пойти на ухудшение суммарного индекса, если максимальный из индексов команд будет меньше 8.

Здесь уместно напомнить, что в задаче оптимизации можно поставить только одну цель. В случае же, если нужно достичь нескольких целей приходится создавать некий синтетический показатель. Либо, кроме главной цели, задавать дополнительные ограничения, направленные на получение не слишком плохого результата по другим вашим требованиям. В данной задаче мы были заинтересованы, чтобы индексы всех пар были минимальными. Так как поставить такую задачу нельзя, использовали синтетический показатель – суммарный индекс. Однако полученное решение нас не устраивает, поэтому остается только один путь – добавить новые ограничения.

Попробуем потребовать, чтобы ни один индекс совместимости команд не превышал 6: I2:I7<=6. Добавляем это ограничение в список Поиска решения и запускаем на выполнение.

Первое, на что следует обратить внимание, это факт, что требуемое решение найдено. Теперь рассмотрим полученное решение внимательней (Рис. 74.).

Рис. 74.

При ближайшем рассмотрении оказывается, что это не совсем то, чего мы ожидали. Более того, это решение не соответствует никакой реальной ситуации,

ведь взвешивать индексы совместимости бессмысленно. Команда с плохим индексом совместимости работает плохо, пусть даже время ее работы невелико.

Но почему получилось решение не в целых числах, если транспортный алгоритм оперирует целыми значениями? Очевидно потому, что Поиск решения вовсе и не использовал транспортный алгоритм. Для поиска решения этой задачи использован стандартный симплекс-метод, потому и получились дробные величины назначений.

В задачах линейной оптимизации для «борьбы» с нецелыми решениями мы использовали целые или двоичные ограничения на переменные. Поступим здесь так же, добавим условие, что все переменные – двоичные (0 или 1) и снова попробуем решить задачу (Рис. 75).

Рис. 75

В данном случае решение так же найдено и теперь удовлетворяет всем нашим ожиданиям. Да, максимальный коэффициент 6. Да, все назначения либо 0, либо 1. И, наконец, суммарный индекс выше, чем в оптимальном решении, полученном нами ранее.

Задача решена. Но давайте проделаем еще небольшое исследование.

Если проверить в исходной таблице индексов совместимости команд минимальные индексы совместимости для каждого техника-программиста и специалиста по маркетингу, то можно увидеть, что самые большие индексы (из минимальных!) равны 4. Это означает, что в принципе, может существовать решение, где все коэффициенты не хуже 4!

По той же таблице можно проанализировать, действительно ли такое решение возможно. Однако, во-первых, быстрее изменить ограничение в Поиске решения и получить ответ автоматически, а во-вторых, все равно для большой таблицы такой анализ «вручную» невозможен. Поэтому изменим ограничение I2:I7<=6 на I2:I7<=4 и снова поищем решение.

Увы, Поиск решения сообщает, что решение не найдено. Это означает, что нельзя назначить 6 пар так, чтобы коэффициенты были не хуже 4. А если не хуже

5?

Проверяем и убеждаемся, что такого решения тоже не существует. Придется остановиться на коэффициентах не хуже 6.