
- •Краткое содержание
- •Полный список примеров, задач и кейсов
- •Предисловие
- •Благодарности
- •Оптимизация в условиях полной определенности
- •1. Метод линейной оптимизации
- •Теоретические замечания.
- •Приемы решения задач
- •1.П-1. Фирма «Фасад»
- •Решение задачи.
- •1.П-2. Компания “Черные каски”
- •Решение задачи.
- •1.П-3. Сталепрокатный завод
- •Решение задачи.
- •1.П-4. На кондитерской фабрике. (Кейс)
- •Анализ Действия 1-го.
- •Действие 2-е. Жаль…, ведь мы все так любим «Батончик»!
- •Анализ Действия 2-го.
- •Дейчтвие 3-е. Проблема учета постоянных издержек
- •Анализ Действия 3-его.
- •1.П-5. Оптимизация производства на заводе «Прогресс» (Кейс)
- •Действие 1-е. Оптимальный план.
- •Первый шаг анализа
- •Второй шаг анализа (Предложение добросовестного рабочего)
- •Четвертый шаг анализа
- •Пятый шаг анализа
- •Анализ Действия 1-го.
- •1.П-6. Аренда с предоплатой
- •Решение задачи.
- •1.П-7. Большой портфель
- •Решение задачи.
- •Задачи для самостоятельного решения
- •1.1. Планирование производства
- •1.1. Три магнитофона
- •1.2. Ферма
- •1.3. Мебельная фабрика
- •1.4. Смешивание соков
- •1.5. Пять типов продукции
- •1.6. Корпорация «Тополь»
- •1.8. Выпуск процессоров
- •1.9. Предприятие в Энске
- •1.10. Электронные переключатели
- •1.11. Фермер Билл Петрушкин
- •1.13. Предприятие «Высокий октан»
- •1.14. Корпорация «Ветер»
- •1.15. Компания «Подмосковная электроника»
- •1.16. Компания «Пауэр Кулинг»
- •1.17. Добыча руды в компании “Седьмой круг”
- •1.18. Детские велосипеды
- •1.19. Горнопромышленная компания “Белые каски”
- •1.20. Предприятие Танти Мару
- •1.21. Очистка нефти
- •1.23. План ремонта станков
- •1.25. Бакалейная лавка
- •1.26. Сухофрукты
- •1.27. Джинсовая одежда
- •1.28. Сэндвичи Жаннет
- •1.29. Компания «Корвет»
- •1.30. Фильм! Фильм! Фильм!!!
- •1.31. Предприятие «Маяк»
- •1.32. Англия, Франция и Испания
- •1.2. Планы закупок
- •1.33. Том, Дик и Джерри
- •1.35. Универсальный магазин
- •1.36. Торговая фирма «Одежда не для всех»
- •1.37. Торговая фирма «Одежда для всех»
- •1.38. Оптовая торговля замороженными овощами
- •1.3. Реклама и маркетинг
- •1.40. Рекламная компания
- •1.41. Эластичность спроса
- •1.42. Фирма «JL»
- •1.43. Корпорация «Фарма Лаб» (бизнес-кейс)
- •1.45. Индекс цен на молочные продукты
- •1.4. Оптимальный состав
- •1.46. Собачья еда
- •1.47. Свиноферма
- •1.48. Фармацевтическая компания
- •1.49. Пять предприятий
- •1.51. Школьные обеды
- •1.5. Финансы
- •1.53. Банк и 6 проектов
- •1.54. Комитет планирования
- •1.55. Инвестиционный бюджет
- •1.56. Консервативный инвестор
- •1.57. Портфель инвестиций
- •1.58. Дистрибьюторская компьютерная фирма
- •1.59. Инвестор и 5 проектов
- •1.60. Частный инвестор
- •1.61. Сара Вильямс
- •1.62. Оценка прибыльности цеха бухгалтерией
- •1.63. Аренда с ежемесячными выплатами
- •1.64. Сертификаты
- •1.65. Компания «СуперИнвест»
- •1.66. Планирование финансового потока
- •1.6. Расписания и графики выполнения заказов на производстве
- •Приемы решения задач
- •1.П-8. Банк «Простор»
- •Решение задачи.
- •1.П-9. Последовательность выполнения заказов
- •Решение задачи.
- •Задачи для самостоятельного решения
- •1.68. “Ясный перец”
- •1.71. Электроэнергия
- •1.72. Последовательность обработки деталей на двух станках
- •1.73. Последовательность обработки деталей на трех станках
- •2. Транспортные задачи и логистика; задачи о назначениях и отборе.
- •Теоретические замечания.
- •Транспортная задача
- •Несбалансированность в транспортной задаче
- •Задача о назначениях
- •Задачи оптимизации логистики и цепочек поставок.
- •Приемы решения задач
- •2.П-1. Дорстрой
- •Решение задачи.
- •2.П-2. Поставки двух видов продуктов
- •Решение задачи.
- •2.П-3. Компью-Нет
- •Решение задачи.
- •2.П-4. Распределение аудиторов по фирмам
- •Решение задачи.
- •2.П-5. Заводы ЖБИ
- •Решение задачи.
- •2.П-6. Две бригады
- •Решение задачи.
- •2.П-7. Отделочный камень для коттеджей (Кейс)
- •Анализ кейса.
- •2.П-8. Цепочка поставок компании «НАЦПРОДУКТ» (Кейс)
- •Действие 1-е: Постановка задач оптимизации.
- •Анализ действия 1 кейса.
- •Определение оптимального плана закупок
- •Определение оптимального плана перевозок
- •Действие 2-е: Оптимизация и здравый смысл.
- •Анализ действия 2 кейса.
- •Действие 3-e: Интегрированный план для цепочки поставок
- •Анализ действия 3 кейса.
- •2.П-9. Фирма «Хороший хозяин»
- •Решение задачи.
- •Задачи для самостоятельного решения
- •2.1. Логистика
- •2.1. Транспортный отдел
- •2.2. Транспортные издержки
- •2.3. Поставки со складов
- •2.4. Дефицит товара
- •2.5. Дорожное строительство
- •2.6. Подготовка к отопительному сезону
- •2.7. Перевозка контейнеров
- •2.9. Поставки
- •2.10. Ремонт автодорог
- •2.11. Слишком много поставщиков
- •2.12. Производственные площадки компании «Воздух»
- •2.13. Перевозки двух продуктов
- •2.14. Перевозки трех продуктов
- •2.15. Многопродуктовая задача
- •2.16. Транспортировка через промежуточные склады
- •2.17. Два завода
- •2.18. Грузовой самолет
- •2.22. Школьные перевозки
- •2.23. Два груза разных объемов
- •2.24. Поставки отопительного оборудования
- •2.25. Воздушные перевозки.
- •2.26. Рейс машины инкассатора
- •2.2. Оптимальные назначения и отбор
- •2.27. 7 команд
- •2.28. 8 команд с проблемой
- •2.29. 9 команд
- •2.30. Олимпийские игры
- •2.31. Назначение слесарей
- •2.32. Отбор специалистов и составление команд
- •2.33. Выбор мест для складов
- •2.34. Распределение оптовиков
- •2.35. Назначение центров снабжения
- •2.36. Склады для компании «Чистые материалы»
- •2.37. Отбор и расстановка рабочих
- •2.38. Дефицит рабочих
- •2.39. Запасная бригада
- •2.40. На стройках МТС
- •2.41. Назначение бригад ремонтников
- •2.43. Проблема мастера
- •2.44. Закупки для компании «Южный производитель»
- •3. Планирование и анализ проектов
- •Теоретические замечания.
- •Приемы решения задач.
- •3.П-1. Обеспечение заданных сроков за счет сверхурочных
- •Решение задачи.
- •3.П-2. Предел еженедельного финансирования проекта.
- •Решение задачи.
- •3.П-3. Проект Омикрон
- •Решение задачи.
- •3.П-4. Научно-просветительский центр планирования семьи в Нигерии.
- •Задачи для самостоятельного решения
- •3.1. Строительный проект
- •3.2. Новый ресторан МакЛуммокс
- •3.3. Консалтинговый проект для «Чайна ОллПродакт».
- •3.4. Срыв сроков начала работ субподрядчиком.
- •3.5. Автомобиль 007
- •3.6. Строительство торгового центра
- •3.7. Проект компании МегаШоп
- •3.9. Петров и партнеры
- •3.11. Мир женщин
- •3.12. Журнал Червонный Гудок
- •3.13. Проект корпорации «SHARON CONSTRUCTION»
- •4. Оптимальное управление запасами
- •Принятые обозначения и необходимые формулы
- •Теоретические замечания.
- •[S] – денежная единица/на один заказ.
- •Модель экономичного размера заказа
- •Основные допущения и параметры модели
- •Оптимальная частота заказа для группы товаров.
- •Модель производства оптимальной партии продукции
- •Ограничения модели экономичного размера заказа (партии продукции) и возможность их преодоления.
- •Приемы решения задач.
- •4.П-1. Выбор поставщика
- •Решение задачи.
- •4.П-2. Строительная фирма
- •Решение задачи.
- •4.П-3. Лов рыбы
- •Решение задачи.
- •Задачи для самостоятельного решения
- •4.1. Выгодное предложение
- •4.2. Гостиница
- •4.3. Чековая лента
- •4.4. Военный госпиталь
- •4.5. Закупки в компании Стоик
- •4.7. Горный автомобиль
- •4.8. Сибирские моторы
- •4.11. Совхоз Чапаевец
- •4.13. Крыша
- •4.14. Предприятие АСЗ
- •4.15. Сеть магазинов «Деловой костюм»
- •5. Комплексное и многопериодное планирование
- •Приемы решения задач.
- •5.П-1. Агрегатный план производственного отдела компании «Вал» (Кейс)
- •Анализ кейса
- •Стратегия 1: Найм и увольнение.
- •Стратегия 2: Сверхурочные и частичная занятость.
- •Стратегия 3: Использование склада.
- •Оптимальная смесь стратегий.
- •Задачи для самостоятельного решения
- •5.1. План для MemoBlink
- •5.3. Ферма Бэрримора
- •5.4. Горные лыжи
- •5.6. Компания АгроМашЗавод
- •5.7. Компания «Лем и сыновья»
- •5.8. График доставки
- •Методы принятия решений в условиях неопределенности и риска
- •Принятые обозначения и необходимые формулы
- •Теоретические замечания
- •Постановка задачи о количественной оценке риска возникновения дефицита и плате за его снижение до заданного уровня.
- •Основные характеристики случайного спроса.
- •Частотное распределение случайного спроса.
- •Нормальное распределение вероятностей.
- •Оценка риска возникновения дефицита по нормальному распределению.
- •Риск возникновения дефицита и уровень обслуживания.
- •Модель фиксированного периода между заказами.
- •Замечание о случайных вариациях времени поставки.
- •Однопериодная модель заказа.
- •Замечание об экономически обоснованном риске дефицита в модели фиксированного размера заказа.
- •Приемы решения задач
- •6.П-1. Магазин сантехники
- •Решение задачи.
- •6.П-2. Оптовые продажи хозтоваров
- •Решение задачи.
- •6.П-3. Новый Электрон
- •Решение задачи.
- •6.П-4. Свежая пресса
- •Решение задачи.
- •6.П-5. Банк «Белый Тигр»
- •Решение задачи.
- •Задачи для самостоятельного решения
- •6.1. Бесконечный горизонт планирования – фиксированный запас
- •6.1. Отель
- •6.2. Офис крупной компании
- •6.3. Сэм управляет запасами
- •6.4. Мастерская
- •6.5. Стадион
- •6.6. “Биг-лайн”
- •6.7. Женский роман
- •6.8. Магазин «Кандела»
- •6.9. Местная станция обслуживания
- •6.10. Грубый Готлиб
- •6.11. Чехлы
- •6.12. Автосервис
- •6.13. Торговля пиломатериалами
- •6.14. Магазин сантехники
- •6.15. Выбор стратегии
- •6.16. Закупка сырья
- •6.17. Магазин «Хозтовары»
- •6.18. Сигнализация
- •6.19. Кухонные гарнитуры
- •6.20. Фармацевтическая компания
- •6.21. Батарейки
- •6.22. Магазин инструментов
- •6.23. Автомобильная секция
- •6.24. Системы водоснабжения
- •6.2. Бесконечный горизонт планирования – фиксированный период
- •6.26. «Пицца-Хат»
- •6.27. Универсальный магазин
- •6.28. Магазин «Свет»
- •6.29. Гамма Гидры
- •6.30. Универмаг «Приреченский»
- •6.31. Секция универсального магазина
- •6.32. Криминальное чтиво
- •6.33. Мини-Маркет
- •6.3. Однопериодная модель
- •6.35. Футболки
- •6.37. Мясной отдел
- •6.38. Компания «Маски»
- •6.40. Киоск
- •6.41. Расторопный Дмитрий
- •6.42. Бронирование контейнеров
- •6.43. Супермаркет и компания «Хозяюшка»
- •6.44. Отделение банка
- •6.45. Университет
- •6.46. Финансирование проекта
- •7. Выбор альтернатив.
- •Основные формулы теории вероятностей
- •Теоретические замечания.
- •Таблица выигрышей и потерь.
- •Принятие решений в условиях полной неопределенности
- •Принятие решений в условиях риска.
- •Стоимость совершенной информации.
- •Анализ устойчивости выбора оптимальной альтернативы для компании «Энергия палеолита».
- •Дерево альтернатив
- •Анализ устойчивости выбора оптимальной альтернативы по дереву альтернатив для компании «Вольный полет».
- •Переоценка вероятностей сценариев будущего в свете дополнительной информации. Стоимость несовершенной информации.
- •Приемы решения задач
- •7.П-1. Производитель снегоходов
- •Решение задачи.
- •7.П-2. Дефектные комплектующие
- •Решение задачи.
- •Задачи для самостоятельного решения
- •Простые сценарии развития событий
- •7.1. Производитель аэросаней
- •7.2. Оптовый склад хозяйственных товаров
- •7.3. Электротермометры
- •7.4. Хоз-маркет
- •7.5. Обувной отдел
- •7.6. Зеленщица
- •7.7. Маленькая кондитерская
- •7.8. Тракторы и СХ Орудия Барни
- •7.9. Переменный спрос
- •7.10. Супермаски
- •7.11. Компьютерная школа
- •7.12. Оптовая база
- •7.13. Елки-палки
- •7.14. Подготовка к зиме
- •7.15. Центр Компьютерного Тренинга
- •7.16. Производственная линия
- •7.17. Кредит
- •7.18. Две стратегии
- •7.19. Новый магазин
- •7.20. Турфирма «Улет»
- •7.21. Курортное местечко
- •Анализ цепочек событий
- •7.24. Парфюмерная компания
- •7.25. Производство ЭЛТ
- •7.27. Биохимическая лаборатория
- •7.30. Компания "Обуем всех"
- •7.31. Консалтинговая служба
- •7.32. Семейная инвестиционная проблема (бизнес-кейс)
- •7.33. Пекарня
- •7.34. Новый бизнес
- •7.36. Ипотечный фонд
- •7.37. Дворец-строй
- •7.38. Большая нефть
- •7.39. ОбувьСити
- •7.40. Золотой рудник
- •7.41. Риэлторская фирма г. Сидорова
- •8. Управление проектами с учетом случайных вариаций времени выполнения стадий
- •Теоретические замечания.
- •Приемы решения задач.
- •8.П-1. Проект «Снеси-Построй»
- •Задачи для самостоятельного решения
- •8.1. Простой проект
- •8.2. Проект рекрутинговой компании
- •8.3. Полная релаксация
- •9. Оценка эффективности систем массового обслуживания и их оптимизация
- •Теоретическое введение.
- •Коммунальные платежи в отделении сбербанка.
- •Пуассоновский поток заявок.
- •Усредненные характеристики работы системы массового обслуживания.
- •Классификация систем массового обслуживания
- •Расчеты характеристик СМО с помощью теории очередей.
- •Приемы решения задач.
- •9.П-1. Банкоматы
- •Решение задачи.
- •9.П-2. Кафе в парке отдыха
- •Решение задачи.
- •9.П-3. Такси по телефону
- •Решение задачи.
- •Задачи для самостоятельного решения
- •9.1. Телефонная система заказа билетов
- •9.2. Таможенный пункт
- •9.3. Большой цех
- •9.4. Приемная
- •9.5. Ресторан «Ешь вволю»
- •9.6. Торговля по каталогам
- •9.7. Таможенный досмотр
- •9.8. Бармен
- •9.9. Стоматологическая поликлиника (бизнес-кейс)
- •9.10. Парикмахерская
- •9.11. Бери и кати
- •9.12. Трасса Е95
- •9.13. Лодочная станция
- •9.14. Погрузка кирпича.
- •9.15. Бар «Аэродром»
- •9.16. Парк аттракционов
- •9.17. Офис
- •9.18. Аттракционы в парке отдыха
- •9.19. Колониальные товары
- •9.20. Мир цветов
- •9.21. Магазин сети «Шамбала»
- •9.22. Кафе «Золотая форель»
- •9.23. Серфинг
- •9.24. Радио-такси
- •9.26. Станки-автоматы
- •9.27. Полиграфическая компания
- •9.28. Кофе для преподавателя
- •9.29. Прядильная мастерская
- •9.30. Тамагочи
- •9.32. Полный порядок
- •9.33. Виртуальный друг
- •9.34. Завод научного приборостроения
- •9.35. Вязальные станки
- •Ответы к задачам
- •Оптимизация в условиях полной определенности
- •Метод линейной оптимизации.
- •1.2 Ферма
- •1.3 Мебельная фабрика
- •1.4 Смешивание соков
- •1.5 Пять типов продукции
- •1.6 Корпорация «Тополь»
- •1.9 Предприятие в Энске.
- •1.11 Фермер Билл Петрушкин
- •1.13 Предприятие «Высокий октан»
- •1.14 Корпорация «Ветер»
- •1.15 Компания «Подмосковная электроника»
- •1.16 Компания «Подмосковная электроника»
- •1.17 Добыча руды в компании “Седьмой круг”
- •1.18 Детские велосипеды
- •1.19 Горнопромышленная компания “Белые каски”
- •1.20 Предприятие Танти Мару
- •1.21 Очистка нефти
- •1.22 Производство минеральных плит
- •1.23 План ремонта станков
- •1.25 Бакалейная лавка
- •1.26 Сухофрукты
- •1.27 Джинсовая одежда
- •1.28 Сэндвичи Жаннет
- •1.29 Компания «Корвет»
- •1.30 Фильм! Фильм! Фильм!!!
- •1.31 Предприятие «Маяк»
- •1.32 Англия, Франция и Испания
- •1.33 Том, Дик и Джерри
- •1.34 Поставки химического сырья
- •1.36 Торговая фирма «Одежда не для всех»
- •1.38 Оптовая торговля замороженными овощами
- •1.39 Корпорация «Природный газ»
- •1.40 Рекламная компания
- •1.41 Эластичность спроса
- •1.42 Фирма «JL»
- •1.45 Индекс цен на молочные продукты
- •1.46 Собачья еда
- •1.47 Свиноферма
- •1.48 Фармацевтическая компания
- •1.51 Школьные обеды
- •1.53 Банк и 6 проект
- •1.56 Консервативный инвестор
- •1.58 Дистрибьюторская компьютерная фирма
- •1.60 Частный инвестор
- •1.61 Сара Вильямс
- •1.62 Оценка прибыльности цеха бухгалтерией
- •1.63 Аренда с ежемесячными выплатами
- •1.64 Сертификаты
- •1.65 Компания «СуперИнвест»
- •1.67 «Дом-строй»
- •1.68 “Ясный перец”
- •1.71 Электроэнергия
- •1.72 Последовательность обработки деталей на двух станках
- •1.73 Последовательность обработки деталей на трех станках
- •Транспортные задачи и логистика; задачи о назначениях и отборе
- •2.1 Транспортный отдел
- •2.2 Транспортные издержки
- •2.3 Поставки со складов
- •2.4 Дефицит товара
- •2.5 Дорожное строительство
- •2.6 Подготовка к отопительному сезону
- •2.7 Перевозка контейнеров
- •2.9 Поставки
- •2.10 Ремонт автодорог
- •2.11 Слишком много поставщиков
- •2.12 Производственные площадки компании «Воздух»
- •2.13 Перевозки двух продуктов
- •2.14 Перевозки трех продуктов
- •2.15 Многопродуктовая задача
- •2.16 Транспортировка через промежуточные склады
- •2.17 Два завода
- •2.22 Школьные перевозки
- •2.23 Два груза разных объемов
- •2.24 Поставки отопительного оборудования
- •2.25 Воздушные перевозки.
- •2.26 Рейс машины инкассатора
- •2.27 7 команд
- •2.28 8 команд с проблемой
- •2.29 9 команд
- •2.30 Олимпийские игры
- •2.31 Назначение слесарей
- •2.32 Отбор специалистов и составление команд
- •2.33 1:1:2:7: Выбор мест для складов
- •2.34 Распределение оптовиков
- •2.35 Назначение центров снабжения
- •2.36 Склады для компании «Чистые материалы»
- •2.37 Отбор и расстановка рабочих
- •2.38 Дефицит рабочих
- •2.39 1:2:2:13. Запасная бригада
- •2.40 На стройках МТС
- •2.41 Назначение бригад ремонтников
- •2.43 Проблема мастера
- •2.44 Закупки для компании «Южный производитель»
- •Планирование и анализ проектов
- •3.1 Строительный проект
- •3.2 Новый ресторан МакЛуммокс
- •3.3 Консалтинговый проект для «Чайна ОллПродакт».
- •3.4 Срыв сроков начала работ субподрядчиком.
- •3.5 Автомобиль 007
- •3.6 Строительство торгового центра
- •3.7 Строительство торгового центра
- •3.9 Петров и партнеры
- •3.11 Мир женщин
- •3.12 Журнал Червонный Гудок
- •3.13 Проект корпорации «SHARON CONSTRUCTION»
- •Оптимальное управление запасами
- •4.2 Гостиница
- •4.3 Чековая лента
- •4.5 Закупки в компании Стоик
- •4.7 Горный автомобиль
- •4.8 Сибирские моторы
- •4.10 ЖК-панели
- •4.11 Совхоз Чапаевец
- •4.13 Крыша
- •4.14 Предприятие АСЗ
- •4.15 Сеть магазинов «Деловой костюм»
- •Комплексное и многопериодное планирование
- •5.1 План для MemoBlink
- •5.3 Ферма Бэрримора
- •5.4 Горные лыжи
- •5.5 Компания Красный молот
- •5.6 Компания АгроМашЗавод
- •5.7 Компания «Лем и сыновья»
- •5.8 График доставки
- •Методы принятия решений в условиях неопределенности и риска
- •Оптимальное управление запасами с учетом случайных вариаций спроса
- •6.1 Отель
- •6.2 Офис крупной компании
- •6.3 Сэм управляет запасами
- •6.4 Мастерская
- •6.5 Стадион
- •6.6 “Биг-лайн”
- •6.7 Женский роман
- •6.8 Магазин «Кандела»
- •6.9 Местная станция обслуживания
- •6.10 Грубый Готлиб
- •6.11 Чехлы
- •6.12 Автосервис
- •6.13 Торговля пиломатериалами
- •6.14 Магазин сантехники
- •6.15 Выбор стратегии
- •6.16 Закупка сырья
- •6.17 Магазин «Хозтовары»
- •6.18 Сигнализация
- •6.19 Кухонные гарнитуры
- •6.20 Фармацевтическая компания
- •6.21 Батарейки
- •6.22 Магазин инструментов
- •6.23 Автомобильная секция
- •6.24 Системы водоснабжения
- •6.26 «Пицца-Хат»
- •6.27 Универсальный магазин
- •6.28 Магазин «Свет»
- •6.29 Гамма Гидры
- •6.30 Универмаг «Приреченский»
- •6.31 Секция универсального магазина
- •6.32 Криминальное чтиво
- •6.33 Мини-Маркет
- •6.35 Футболки
- •6.37 Мясной отдел
- •6.38 Компания «Маски»
- •6.39 Шубы
- •6.40 Киоск
- •6.41 Расторопный Дмитрий
- •6.42 Бронирование контейнеров
- •6.43 Супермаркет и компания «Хозяюшка»
- •6.44 Отделение банка
- •6.45 Университет
- •6.46 Финансирование проекта
- •Выбор альтернатив
- •7.1 Производитель аэросаней
- •7.2 Оптовый склад хозяйственных товаров
- •7.3 Электротермометры
- •7.4 Хоз-маркет
- •7.5 Обувной отдел
- •7.6 Зеленщица
- •7.7 Маленькая кондитерская
- •7.8 Тракторы и СХ Орудия Барни
- •7.9 Переменный спрос
- •7.10 Супермаски
- •7.11 Компьютерная школа
- •7.12 Оптовая база
- •7.13 Елки-палки
- •7.14 Подготовка к зиме
- •7.15 Центр Компьютерного Тренинга
- •7.16 Производственная линия
- •7.17 Кредит
- •7.18 Две стратегии
- •7.19 Новый магазин
- •7.20 Турфирма «Улет»
- •7.21 Курортное местечко
- •7.24 Парфюмерная компания
- •7.25 Производство ЭЛТ
- •7.26 Пробка
- •7.27 Биохимическая лаборатория
- •7.28 Повышение квалификации
- •7.30 Компания "Обуем всех"
- •7.31 Консалтинговая служба
- •7.32 Семейная инвестиционная проблема
- •7.33 Пекарня
- •7.34 Новый бизнес
- •7.36 Ипотечный фонд
- •7.37 Дворец-строй
- •7.38 Большая нефть
- •7.39 ОбувьСити
- •7.40 Золотой рудник
- •7.41 Риэлторская фирма г. Сидорова
- •7.42 Покупка магазина
- •Управление проектами с учетом случайных вариаций времени выполнения стадий
- •8.1 Простой проект
- •8.2 Проект рекрутинговой компании
- •8.3 Полная релаксация
- •Оценка эффективности систем массового обслуживания и их оптимизация
- •9.1 Телефонная система заказа билетов
- •9.2 Таможенный пункт
- •9.3 Большой цех
- •9.4 Приемная
- •9.5 Ресторан «Ешь вволю»
- •9.6 Торговля по каталогам
- •9.7 Таможенный досмотр
- •9.8 Бармен
- •9.9 Стоматологическая поликлиника
- •9.10 Парикмахерская
- •9.11 Бери и кати
- •9.12 Трасса Е95
- •9.13 Лодочная станция
- •9.14 Погрузка кирпича.
- •9.15 Бар «Аэродром»
- •9.16 Парк аттракционов
- •9.17 Офис
- •9.18 Аттракционы в парке отдыха
- •9.19 Колониальные товары
- •9.20 Мир цветов
- •9.21 Магазин сети «Шамбала»
- •9.22 Кафе «Золотая форель»
- •9.23 Серфинг
- •9.24 Радио-такси
- •9.26 Станки-автоматы
- •9.27 Полиграфическая компания
- •9.28 Кофе для преподавателя
- •9.29 Прядильная мастерская
- •9.30 Тамагочи
- •9.32 Полный порядок
- •9.33 Виртуальный друг
- •9.34 Завод научного приборостроения
- •9.35 Вязальные станки
- •Глоссарий
количественных методов и технической реализации оптимизационных моделей, а в области человеческих и информационных проблем управления.
Во-первых, как это и отражено в тексте кейса, люди, работающие в том или ином функциональном подразделении компании, склонны считать, что в их отделе дела идут вполне хорошо, а проблемы компании коренятся в неудовлетворительной работе коллег из других функциональных подразделений. Феофан ожидает от Макса более совершенного плана закупок, а не перевозок, а Боб рекомендует ему «пойти и помочь Феофану». Инициировать процесс изменения принятия решений или каких-либо организационных изменений в компании может только топ-менеджмент. Поэтому критическим условием для начала процесса интеграции цепочки поставок и оптимизации планирования является наличие убежденности топ-менеджеров в существовании проблемы, необходимости изменений.
Во-вторых, любое усечение функций того или иного подразделения, а тем более передача другим лицам ключевой функции принятия решений, вызовет сопротивление руководителей подразделений и персонала, поскольку люди будут воспринимать это как первый шаг к собственному увольнению. Боб сейчас – это одна из ключевых фигур в компании потому, что он принимает решение, с кем из потенциальных поставщиков заключить договор, а с кем – нет, и передача этой функции Максу или компьютеру вряд ли ему понравится. Необходимо должным образом мотивировать людей – участников процесса изменений, убедить их в том, что снижение издержек и увеличение прибыльности компании благотворно скажется на каждом из них (и вести изменения соответственно).
В-третьих, для построения, правильного функционирования оптимизационной модели и генерирования результатов, полезных для принятия управленческих решений, необходимы объективные данные, адекватные построенной модели. Вместе с тем, несмотря на наличие в организации весьма совершенных информационных систем, консультанты-практики, нередко, испытывают сложности с получением необходимых для модели данных. Причина в том, что при проектировании и настройке информационной системы, вопреки заклинаниям специалистов по ИСУ, менеджеры ориентируются на организационную структуру и способ ведения дела «как есть», а не «как должно быть» в оптимальной модели бизнес-процессов.
Наверняка можно назвать еще много причин, препятствующих внедрению оптимизационных моделей в практику управления и интегрированию бизнеспроцессов. Однако, все эти вопросы, очевидно, выходят за рамки настоящего сборника. Повторим, однако, что со стороны количественных методов и существующих в настоящее время оптимизационных инструментов ограничений для этой деятельности практически нет.
2.П-9. Фирма «Хороший хозяин»
Фирма «Хороший хозяин» имеет сеть из 12 магазинов бытовых инструментов и оборудования в крупном городе. Все магазины снабжаются одним складом. Доставка осуществляется одной автомашиной, принадлежащей фирме, и проводится раз в два дня. При этом на складе формируется груз, который всегда можно развезти за одну ездку. Автомашина забирает его со склада и развозит по магазинам, объезжая их по очереди.
Зайцев М.Г., Варюхин С.Е. |
231 |
Пользуясь подробной картой города можно нарисовать все возможные участки пути между магазинами и складом. При 12 пунктах, которые должен посетить автомобиль, и с учетом того, что он должен вернуться обратно на склад, получается 78 различных участков пути (количество клеток выше диагонали в приведенной таблице). Протяженность всех этих участков приведена в таблице.
Расстояния, |
Б |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
км |
|
|
|
|
|
|
|
|
|
|
|
|
|
База |
|
5 |
8 |
6 |
35 |
9 |
13 |
27 |
23 |
19 |
14 |
20 |
20 |
Маг. № 1 |
5 |
|
13 |
5 |
37 |
14 |
18 |
28 |
28 |
24 |
19 |
21 |
25 |
Маг. № 2 |
8 |
13 |
|
9 |
39 |
7 |
8 |
33 |
17 |
12 |
9 |
26 |
20 |
Маг. № 3 |
6 |
5 |
9 |
|
40 |
13 |
16 |
32 |
26 |
21 |
17 |
25 |
26 |
Маг. № 4 |
35 |
37 |
39 |
40 |
|
32 |
34 |
12 |
37 |
37 |
33 |
17 |
21 |
Маг. № 5 |
9 |
14 |
7 |
13 |
32 |
|
4 |
28 |
15 |
10 |
5 |
22 |
14 |
Маг. № 6 |
13 |
18 |
8 |
16 |
34 |
4 |
|
31 |
10 |
6 |
1 |
25 |
14 |
Маг. № 7 |
27 |
28 |
33 |
32 |
12 |
28 |
31 |
|
37 |
36 |
30 |
7 |
22 |
Маг. № 8 |
23 |
28 |
17 |
26 |
37 |
15 |
10 |
37 |
|
5 |
9 |
33 |
16 |
Маг. № 9 |
19 |
24 |
12 |
21 |
37 |
10 |
6 |
36 |
5 |
|
6 |
30 |
16 |
Маг. № 10 |
14 |
19 |
9 |
17 |
33 |
5 |
1 |
30 |
9 |
6 |
|
25 |
12 |
Маг. № 11 |
20 |
21 |
26 |
25 |
17 |
22 |
25 |
7 |
33 |
30 |
25 |
|
18 |
Маг. № 12 |
20 |
25 |
20 |
26 |
21 |
14 |
14 |
22 |
16 |
16 |
12 |
18 |
|
a.Сформулируйте задачу линейной оптимизации, которая позволяет найти самый короткий по общей протяженности маршрут для автомашины, позволяющий объехать все 12 магазинов. Никаких ограничений на порядок объезда магазинов нет. Машина должна выехать со склада и на него же вернуться.
b.Предположим, что на этот раз магазин №2 не нуждается в доставке товара. Какой маршрут теперь будет самым коротким.
Решение задачи.
Умудренный опытом читатель, может подумать, что предложение решить подобную задачу – злая шутка. Ведь это знаменитая задача коммивояжера, классический пример применения метода динамического программирования, на котором десятилетиями оттачивают свое искусство программисты. Мы же не договаривались писать программы для компьютера!
На самом деле, наша цель заключается в том, чтобы сформулировать и решить с помощью «Поиска решения» задачу линейной (целочисленной) оптимизации, соответствующую задаче коммивояжера. При этом мы не будем настаивать, что метод решения таких задач, с помощью надстройки «Поиск решения», является более эффективным, чем динамическое программирование. Просто для большинства пользователей сегодня он может оказаться более доступным.
Для начала смело заверим читателя, что сформулировать такую задачу можно! Такая уверенность сильно помогает при решении.
Через некоторое время после того, как вы решительно возьметесь за постановку задачи, вам покажется, что сформулировать задачу не так уж и несложно. Ведь в одной из разобранных нами в первом разделе задач как раз

формируется последовательность выполнения заказов, приводящая к наименьшим задержкам в выполнении. А здесь мы составим последовательность объезда магазинов и минимизируем общий путь - и все !?
К сожалению все не так просто. Да, в определенном смысле эти задачи родственны. Но в задаче о порядке выполнения заказов длительность выполнения заказа не зависела от того, какой заказ выполнялся перед ним. В данной же задаче расстояние, которое грузовик пройдет до очередного магазина, зависит от того, какой магазин он посетил перед этим. В таких условиях не удается так же просто вычислить расстояние до очередного магазина, как в предыдущей задаче.
Вместо этого можно попробовать просто составить табличку 13х13 переменных, соответствующую таблице расстояний (база и 12 магазинов) и расставить в этой табличке 13 единиц, которые будут показывать, какие переезды между магазинами выбраны. Если теперь применить функцию =СУММПРОИЗВ( ) к этим двум таблицам, то мы сразу получим общее расстояние, которое проехал грузовик. Таким образом задача линейной целочисленной оптимизации практически составлена (Рис. 111).
1 |
A |
B |
C D E F G H I J K L M N O |
P |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
=СУММПРОИЗВ( |
3 |
0 |
База |
## |
5 |
8 |
6 |
35 |
9 |
13 |
27 |
23 |
19 |
14 |
20 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C3:O3;C18:O18) |
4 |
1 |
Мг 1 |
5 |
## |
13 |
5 |
37 |
14 |
18 |
28 |
28 |
24 |
19 |
21 |
25 |
0 |
5 |
2 |
Мг 2 |
8 |
13 |
## |
9 |
39 |
7 |
8 |
33 |
17 |
12 |
9 |
26 |
20 |
0 |
6 |
3 |
Мг 3 |
6 |
5 |
9 |
## |
40 |
13 |
16 |
32 |
26 |
21 |
17 |
25 |
26 |
0 |
7 |
4 |
Мг 4 |
35 |
37 |
39 |
40 |
## |
32 |
34 |
12 |
37 |
37 |
33 |
17 |
21 |
0 |
… … …. … … … … … … … … … … … … … |
…. |
|||||||||||||||
15 |
12 |
Мг 12 |
20 |
25 |
20 |
26 |
21 |
14 |
14 |
22 |
16 |
16 |
12 |
18 |
## |
0 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
17 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
18 |
|
База |
|
|
|
|
|
|
|
|
|
|
|
|
|
=СУММ(C18:O18) |
19 |
|
Мг 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
20 |
|
Мг 2 |
|
|
|
Переменные |
|
|
|
|
|
0 |
||||
21 |
|
Мг 3 |
|
|
|
|
|
|
|
|
0 |
|||||
22 |
|
Мг 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
… |
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
30 |
|
Мг 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
31 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
=СУММ(O18:O30) |
|
|
|
Рис. 111 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Однако здесь нас также поджидает глубокое разочарование. Дело в том, |
||||||||||||||
что чаще всего предлагаемый Поиском решения маршрут не является кольцевым. |
||||||||||||||||
Зайцев М.Г., Варюхин С.Е. |
233 |
|
|
|
|
Рис. 112
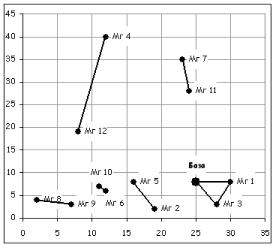
Т.е. какая-то часть маршрута действительно соответствует выезду из базы, посещению нескольких магазинов и возвращению назад - База-> Магазин №3 -> Магазин №1-> База. Но большая часть предложенного маршрута имеет вид: Мг 2 -> Мг 5-> Мг 2, или Мг 7 -> Мг 11 -> Мг 7 (Рис. 113 и Рис. 112).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
0 |
|
База |
## |
5 |
8 |
6 |
35 |
9 |
13 |
27 |
23 |
19 |
14 |
20 |
20 |
5 |
1 |
|
Мг 1 |
5 |
## |
13 |
5 |
37 |
14 |
18 |
28 |
28 |
24 |
19 |
21 |
25 |
5 |
2 |
|
Мг 2 |
8 |
13 |
## |
9 |
39 |
7 |
8 |
33 |
17 |
12 |
9 |
26 |
20 |
7 |
3 |
|
Мг 3 |
6 |
5 |
9 |
## |
40 |
13 |
16 |
32 |
26 |
21 |
17 |
25 |
26 |
6 |
4 |
|
Мг 4 |
35 |
37 |
39 |
40 |
## |
32 |
34 |
12 |
37 |
37 |
33 |
17 |
21 |
21 |
5 |
|
Мг 5 |
9 |
14 |
7 |
13 |
32 |
## |
4 |
28 |
15 |
10 |
5 |
22 |
14 |
7 |
6 |
|
Мг 6 |
13 |
18 |
8 |
16 |
34 |
4 |
## |
31 |
10 |
6 |
1 |
25 |
14 |
1 |
7 |
|
Мг 7 |
27 |
28 |
33 |
32 |
12 |
28 |
31 |
## |
37 |
36 |
30 |
7 |
22 |
7 |
8 |
|
Мг 8 |
23 |
28 |
17 |
26 |
37 |
15 |
10 |
37 |
## |
5 |
9 |
33 |
16 |
5 |
9 |
|
Мг 9 |
19 |
24 |
12 |
21 |
37 |
10 |
6 |
36 |
5 |
## |
6 |
30 |
16 |
5 |
10 |
|
Мг 10 |
14 |
19 |
9 |
17 |
33 |
5 |
1 |
30 |
9 |
6 |
## |
25 |
12 |
1 |
11 |
|
Мг 11 |
20 |
21 |
26 |
25 |
17 |
22 |
25 |
7 |
33 |
30 |
25 |
## |
18 |
7 |
12 |
|
Мг 12 |
20 |
25 |
20 |
26 |
21 |
14 |
14 |
22 |
16 |
16 |
12 |
18 |
## |
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
98 |
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
База |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
Мг 5 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
||
|
|
Мг 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
Мг 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
Мг 9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 10 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Мг 12 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Рис. 113
Разумеется, это вовсе не решение исходной задачи.
Если бы проблема была бы только в маршрутах вида Мг 7 -> Мг 11 -> Мг 7, ее легко было бы устранить. В самом деле, при наличии таких маршрутов в

полученном решении соответствующие элементы таблицы переменных оказываются симметричными относительно диагонали C18-O30. Например, единица, показывающая наличие перевозки, стоит и в ячейке J29 (переезд из Мг 7 в Мг 11), и в ячейке N25 (переезд из Мг 11 в Мг 7), симметричной ячейке J29 относительно диагонали таблицы переменных.
Добавим к нашему решению еще одну таблицу, по размеру совпадающую с таблицей переменных, в которой сложим симметричные относительно диагонали переменные друг с другом.
Это, правда, не делается простым протягиванием. А в задании для «Поиска решения» добавим условие, что все эти суммы меньше или равны 1. Это исключит возвратные маршруты.
После этого запустим надстройку Поиск решения на выполнение и опять проанализируем полученное решение (в таблице на Рис. 114 приведено только полученное решение).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
109 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
База |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
Кл 3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
||
|
Кл 5 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 6 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 7 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
Кл 9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
Кл 10 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Кл 12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Рис. 114
Во-первых, видно, что общая длина маршрута увеличилась с 98 до 109 км. Т.е. введенное ограничение действительно привело к изменению маршрута.
Рис. 115
Зайцев М.Г., Варюхин С.Е. |
235 |
Анализ полученного решения (Рис. 114 и Рис. 115) показывает, что и на этот раз решение не может нас устроить. Получилось три цикла, вместо одного.
Если углубиться в анализ графов (а полученное решение можно назвать несвязным графом), можно создать запрет на циклы длиной в 3 звена и более. На сайте www.HCXL.ru на страничке об этой книге вы можете посмотреть альтернативное решение данной задачи, использующее такой подход.
Здесь же мы приведем более громоздкое, но и более очевидное решение. К тому же оно во многих случаях находится компьютером быстрее.
Придется пойти сложным путем, в частности оказывается, что при этом необходимо использование более продвинутой модели надстройки Поиск решения под названием Large-Scale LP Solver. Эту продвинутую надстройку можно найти на сайте компании-создателя этого инструмента FrontLine System www.solver.com. Надстройку можно скачать бесплатно и пользоваться ею в течение двухнедельного пробного срока.
Этот вариант надстройки позволяет решать задачи с десятками тысяч переменных и ограничений. Именно это нас и интересует, так как в предложенной здесь формулировке задачи линейной целочисленной оптимизации оказывается не менее 1608 переменной. Стандартная версия надстройки «Поиск решения» в MS Excel допускает не более 200 переменных.
Для того, чтобы построить задачу линейной целочисленной оптимизации, дающую верное решение задачи коммивояжера вообще, и нашей задачи в частности, необходимо сформулировать требования к переменным, которые обязательно должны выполняться. Таких требований в общем три:
В первый магазин маршрута объезда автомобиль должен прибыть с базы. Для каждого последующего магазина пунктом, из которого прибыл
автомобиль должен являться предыдущий по порядку посещения магазин.
Из последнего магазина автомобиль должен отправиться обратно на базу. Таким образом на первом шаге мы выбираем 1 из 12 магазинов, в который
поедем с базы (склада), т.е. имеем 12 переменных.
На втором шаге выбираем второй пункт маршрута. Так как мы поедем из выбранного на первом шаге магазина (1 из 12) в другой магазин (вообще говоря тоже 1 из 12, так как заранее неизвестно, какой магазин посещен первым), но не на базу, то для выбора второго пункта посещения необходимо выбрать одно направление поездки из 144 (=12*12) возможных. При этом после выбора нужно будет проверить, что выбор «откуда» прибыл, совпадает с выбором «куда» прибыл, сделанным на предыдущем шаге.
На третьем, четвертом, …, двенадцатом шаге делаем то же самое. Каждый такой выбор добавляет 144 переменных к задаче.
На последнем тринадцатом шаге мы должны вернуться на базу. Для этого нужно выбрать пункт «откуда» автомобиль туда вернется. Это необходимо для вычисления длины маршрута возвращения. Это добавит к задаче еще 12 переменных. Итого получаем 12 + 11* 12*12 + 12 = 1608 переменных.
Мы, однако, не будем так экономить на переменных. Учитывая, что нужно иметь возможность легкой модификации задачи для ответов на дополнительные вопросы без перестройки всей модели, лучше будем строить задачу как более общую. Если, например, мы хотим иметь возможность строить маршруты с промежуточным возвращением на склад, следует на каждом шаге допустить выезд из 12 магазинов и склада (базы) и возможность возвращения в любой из этих 13 пунктов.
Вновой таблице (Рис. 116) приведен пример организации данных для нашей задачи.
Вячейках D36:O168 и C169:C180 содержатся переменные задачи. В данном случае единица в ячейке D36 строки D36:O36 показывает, что первым пунктом посещения после отправления с базы является Мг 1. При этом строка D21:O21 просто дублирует строку D36:O36, а в ячейке R21 по формуле =СУММПРОИЗВ ($D$1:$O$1; D21:O21) вычисляется номер посещенного магазина.

|
Зайцев М.Г., Варюхин С.Е. |
|
|
|
|
|
|
|
|
|
237 |
|||||
|
A B |
C |
D |
E |
F G H I J K L M N O P Q R |
|||||||||||
1 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
2 |
0 |
База |
## |
5 |
8 |
6 |
35 |
9 |
13 |
27 |
23 |
19 |
14 |
20 |
20 |
|
3 |
1 |
Мг 1 |
5 |
## |
13 |
5 |
37 |
14 |
18 |
28 |
28 |
24 |
19 |
21 |
25 |
|
4 |
2 |
Мг 2 |
8 |
13 |
## |
9 |
39 |
7 |
8 |
33 |
17 |
12 |
9 |
26 |
20 |
Таблица |
5 |
3 |
Мг 3 |
6 |
5 |
9 |
## |
40 |
13 |
16 |
32 |
26 |
21 |
17 |
25 |
26 |
взаимных |
6 |
4 |
Мг 4 |
35 |
37 |
39 |
40 |
## |
32 |
34 |
12 |
37 |
37 |
33 |
17 |
21 |
расстояний, км. |
7 |
5 |
Мг 5 |
9 |
14 |
7 |
13 |
32 |
## |
4 |
28 |
15 |
10 |
5 |
22 |
14 |
|
8 |
6 |
Мг 6 |
13 |
18 |
8 |
16 |
34 |
4 |
## |
31 |
10 |
6 |
1 |
25 |
14 |
|
9 |
7 |
Мг 7 |
27 |
28 |
33 |
32 |
12 |
28 |
31 |
## |
37 |
36 |
30 |
7 |
22 |
|
10 |
8 |
Мг 8 |
23 |
28 |
17 |
26 |
37 |
15 |
10 |
37 |
## |
5 |
9 |
33 |
16 |
|
11 |
9 |
Мг 9 |
19 |
24 |
12 |
21 |
37 |
10 |
6 |
36 |
5 |
## |
6 |
30 |
16 |
|
12 |
10 |
Мг 10 |
14 |
19 |
9 |
17 |
33 |
5 |
1 |
30 |
9 |
6 |
## |
25 |
12 |
|
13 |
11 |
Мг 11 |
20 |
21 |
26 |
25 |
17 |
22 |
25 |
7 |
33 |
30 |
25 |
## |
18 |
|
14 |
12 |
Мг 12 |
20 |
25 |
20 |
26 |
21 |
14 |
14 |
22 |
16 |
16 |
12 |
18 |
## |
|
15 |
|
|
|
Расстояния между пунктами маршрута, км |
|
Всего км. |
||||||||||
16 |
|
|
5 |
5 |
9 |
7 |
4 |
1 |
6 |
5 |
16 |
21 |
12 |
7 |
20 |
118 |
17 |
|
0 |
=R21 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
=R33 |
||
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
=СУММ(O36:O180) |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
1 |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
22 |
2 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
3 |
23 |
3 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
24 |
4 |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
=СУММ(D36:O36) |
0 |
1 |
1 |
0 |
||||
|
|
0 |
0 |
0 |
0 |
0 |
||||||||||||
25 |
5 |
|
|
0 |
0 |
0 |
=СУММПРОИЗВ($D$1:$O$1;D21:O21) |
1 |
1 |
0 |
||||||||
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
26 |
6 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
27 |
7 |
|
|
0 |
0 |
=СУММ(D36:D48) |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
||||
|
|
0 |
0 |
0 |
0 |
0 |
||||||||||||
28 |
8 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
29 |
9 |
|
|
0 |
0 |
=СУММ(D109:D120) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
||||
|
|
0 |
0 |
0 |
0 |
0 |
||||||||||||
30 |
10 |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
31 |
11 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
32 |
12 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
33 |
13 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
34 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
35 |
|
|
=СУММ |
|
||||||||||||||
36 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||
|
(D36:O36) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
37 |
1 |
2 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
38 |
2 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
39 |
3 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48 |
12 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
49 |
1 |
3 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
157 |
1 |
12 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
163 |
7 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=СУММ |
|
|
168 |
12 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||
|
|
(D168:O168) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
169 |
1 |
13 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
=C169 |
|
|
170 |
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
=C170 |
|
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
179 |
11 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
180 |
12 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
Рис. 116
Выбор второго пункта посещения делается в ячейках D37:O48. Единица в ячейке F37 показывает, что вторым пунктом выбран Мг 3 (см. номер магазина по этому же столбцу, в котором стоит 1, в ячейке F35). При этом ссылку на номер предыдущего магазина смотрим по этой же строке в ячейке A37. В столбце
P36:P168 считаются суммы по строкам переменных. Эти суммы позволяют с одной стороны задать ограничение на выбор только одного пункта назначения на каждом шаге, а с другой стороны формируют очень нужные нам данные. В самом деле, так как номер строки в соответствии с нумерацией в столбце А показывает, из какого пункта прибыл автомобиль, то столбец P37:P48 должен совпадать со строкой D21:O21. Как вы видите, так оно и есть. Но главное, что этого можно потребовать при поиске решения (в данной, более продвинутой, версии Поиска решения можно сравнивать строки и столбцы)!
Встроке D22:O22 вычисляются суммы по столбцам от D37:D48 до O37:O48, также подытоживающие результаты выбора на втором шаге, для использования их на шаге третьем. Т.е. в строке D22:O22 показано, какой магазин был выбран на втором шаге. Непосредственно для лучшего представления результатов в ячейке R22 по той же формуле =СУММПРОИЗВ ($D$1:$O$1; D22:O22) вычисляется номер посещенного магазина.
Выбор третьего пункта посещения делается в ячейках D49:O60. Снова суммы в столбце P49:P60 должны совпадать со значениями в строке D22:O22, показывающей второй пункт посещения.
Вобщем эта процедура построения таблицы продолжается до выбора 13 пункта без изменений. Как уже отмечалось выше на тринадцатом шаге нужно вернуться в базу, поэтому пункт назначения определен. Для «выбора» предыдущего пункта используем 12 переменных: C169:C180. Собственно говоря, прочие соотношения остаются теми же, только в некоторых местах надобность в суммировании отсутствует, т.к. в сумме имеется только одно слагаемое. Значения ячеек в столбце P169:P180 должны совпасть со значениями в строке D32:O32, что также нужно будет задать в списке ограничений Large-Scale LP Solver’а. Для того, чтобы каждый магазин был выбран в качестве пункта назначения только 1 раз, используются результаты расчетов в ячейках C19:O19. Очевидно следует потребовать, чтобы суммы всех переменных по столбцам равнялись 1, что соответствует выбору каждого магазина один и только один раз.
Чтобы выбрать каждый магазин только 1 раз в качестве предыдущего пункта посещения используем результаты суммирования в столбце Q21:Q33. В каждой из этих ячеек найдены суммы ячеек соответствующие выбору: Мг 1 на шагах 2, 3, 4…12, Мг 2 на шагах 2, 3, 4…12 и т.д. до Мг 12. Если потребовать, чтобы Q21:Q33 = 1, каждый магазин выступит в качестве предыдущего пункта посещения один и только один раз.
Ну и наконец, самое главное – расчет расстояний. Собственно говоря, мы ведь и вводили такое большое количество переменных именно для того, чтобы в каждом пункте легко вычислять, откуда приехали. Поэтому отдельные таблицы переменных для каждого из пунктов посещения дают при умножении на нужную часть таблицы расстояний C2:O14 расстояние очередной поездки. Например в C16 по формуле =СУММПРОИЗВ($C$2:$O$2;$C36:$O36) вычислено расстояние от базы до первого пункта посещения. В ячейках D16:O16 по другой формуле вида =СУММПРОИЗВ($C$3:$O$14;$C37:$O48) вычислено расстояние от первого пункта посещения до второго, от второго до третьего и т.д.
Сумма всех этих расстояний и дает длину маршрута объезда магазинов (Q16), которая в нашей задаче играет роль целевой функции, минимума которой мы хотим добиться.
Остается сформировать задание для Поиска решения. В новой, использованной нами при решении данной задачи, инкарнации этой надстройки это выглядит следующим образом (Рис. 117)

Зайцев М.Г., Варюхин С.Е. |
239 |
Рис. 117
На рисунке снизу от диалогового окна Поиска решения показаны те ограничения, которые не видны в самом окне.
Так же желательно установить большую точность при поиске решения на вкладке Options (Рис. 118)
Рис. 118

Если теперь запустить поиск решения, то спустя 1-3 минуты, в зависимости от мощности процессора, получим то решение, которое и показано в табличке: минимальная длина маршрута 118 км, порядок пунктов посещения -
База (0) 1 |
3 |
2 |
5 |
6 10 9 |
8 12 4 |
7 11 База (0) |
Как вы можете убедиться, это решение отличается от предыдущих вариантов большей длиной. На Рис. 119 приведено изображение оптимального маршрута поездки автомобиля по магазинам.
Рис. 119
Вопрос b.
Разумеется, чтобы ответить на этот вопрос можно было бы перестроить задачу, выбросив из всех расчетов магазин №2. Это заодно уменьшило бы число переменных.
Однако, как мы видели, задача строится довольно долго, а это значит, что вероятность внести ошибку при перестройке задачи довольно велика. Кроме того, полная перестройка таблицы и задачи не в духе MS Excel. Лучше всего было бы добиться нового решения немного изменив данные.
Таким образом, нам нужно получить решение, в котором будет присутствовать фиктивный заезд в магазин №2. Только этот заезд не должен влиять на правильный расчет расстояний и обязан дать нулевой вклад в суммарную длину маршрута.
Этого можно добиться простым способом. Изменим таблицу расстояний так, чтобы места магазина №2 и базы на карте поездок совпадали. Для этого зададим расстояния от магазина №2 до всех пунктов, такими же, как от базы. А расстояние от базы до самого магазина сделаем нулевым. Изменения, которые нужно внести в таблицу расстояний, показаны на Рис. 120.

|
Зайцев М.Г., Варюхин С.Е. |
|
|
|
|
|
|
|
|
|
|
|
241 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
B |
C |
D |
E |
F |
G |
H |
|
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
|
1 |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
2 |
0 |
База |
## |
5 |
0 |
6 |
35 |
9 |
|
13 |
27 |
23 |
19 |
14 |
20 |
20 |
|
|
|
|
3 |
1 |
Мг 1 |
5 |
## |
5 |
5 |
37 |
14 |
|
18 |
28 |
28 |
24 |
19 |
21 |
25 |
|
|
|
|
4 |
2 |
Мг 2 |
0 |
5 |
## |
6 |
35 |
9 |
|
13 |
27 |
23 |
19 |
14 |
20 |
20 |
Таблица |
|||
5 |
3 |
Мг 3 |
6 |
5 |
6 |
## |
40 |
13 |
|
16 |
32 |
26 |
21 |
17 |
25 |
26 |
взаимных |
|
||
6 |
4 |
Мг 4 |
35 |
37 |
35 |
40 |
## |
32 |
|
34 |
12 |
37 |
37 |
33 |
17 |
20 |
расстояний, км. |
|
||
7 |
5 |
Мг 5 |
9 |
14 |
9 |
13 |
32 |
## |
|
4 |
28 |
15 |
10 |
5 |
22 |
14 |
|
|
|
|
8 |
6 |
Мг 6 |
13 |
18 |
13 |
16 |
34 |
4 |
|
## |
31 |
10 |
6 |
1 |
25 |
14 |
|
|
|
|
9 |
7 |
Мг 7 |
27 |
28 |
27 |
32 |
12 |
28 |
|
31 |
## |
37 |
36 |
30 |
7 |
22 |
|
|
|
|
10 |
8 |
Мг 8 |
23 |
28 |
23 |
26 |
37 |
15 |
|
10 |
37 |
## |
5 |
9 |
33 |
16 |
|
|
|
|
11 |
9 |
Мг 9 |
19 |
24 |
19 |
21 |
37 |
10 |
|
6 |
36 |
5 |
## |
6 |
30 |
16 |
|
|
|
|
12 |
10 |
Мг 10 |
14 |
19 |
14 |
17 |
33 |
5 |
|
1 |
30 |
9 |
6 |
## |
25 |
12 |
|
|
|
|
13 |
11 |
Мг 11 |
20 |
21 |
20 |
25 |
17 |
22 |
|
25 |
7 |
33 |
30 |
25 |
## |
18 |
|
|
|
|
14 |
12 |
Мг 12 |
20 |
25 |
20 |
26 |
21 |
14 |
|
14 |
22 |
16 |
16 |
12 |
18 |
## |
|
|
|
|
|
Рис. 120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так |
как |
маршрут |
начинается |
с |
базы |
и |
заканчивается базой, то в |
||||||||||||
оптимальном маршруте магазин №2 окажется либо первым, после выезда, либо последним из посещенных. Чтобы упростить выбор маршрута для Large-Scale LP Solver’а, можно добавить в список ограничений одно простое условие: R21 = 2. Таким образом мы потребуем, чтобы фиктивный заезд в магазин №2 был сделан сразу после выезда с базы. При этом маршрут будет следующим:
База |
2 |
3 |
1 |
11 |
7 |
4 |
12 |
8 |
9 |
10 |
6 |
5 |
База (0) |
|
(0) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Общая длина такого минимального маршрута составит 112 км.
Отметим, что качество поиска довольно сильно зависит от установок точности поиска. Попробуйте обнулить переменные, уменьшить точность и повторить поиск. Вы увидите, что будет найдено не лучшее решение.
