Трёхмерное моделирование

Первые две опции ( и ) позволяют задать направляющий вектор двумя 3D точками. Остальные позволяют выбрать 3D объект, способный сразу определить направляющий вектор.

Для задания направления эквидистанты с тела используется опция:

<G> Выбрать тело (операцию)

Величина смещения эквидистанты указывается в диалоге параметров пути:

<P> Задать параметры элемента

Смещение эквидистанты указывается в параметре “Расстояние” данного диалога.

Здесь же осуществляется (при необходимости) включение режима смещения с доворотом. Для этого достаточно указать в поле параметра “Угол” требуемое значение угла доворота (по умолчанию стоит значение

“0”).

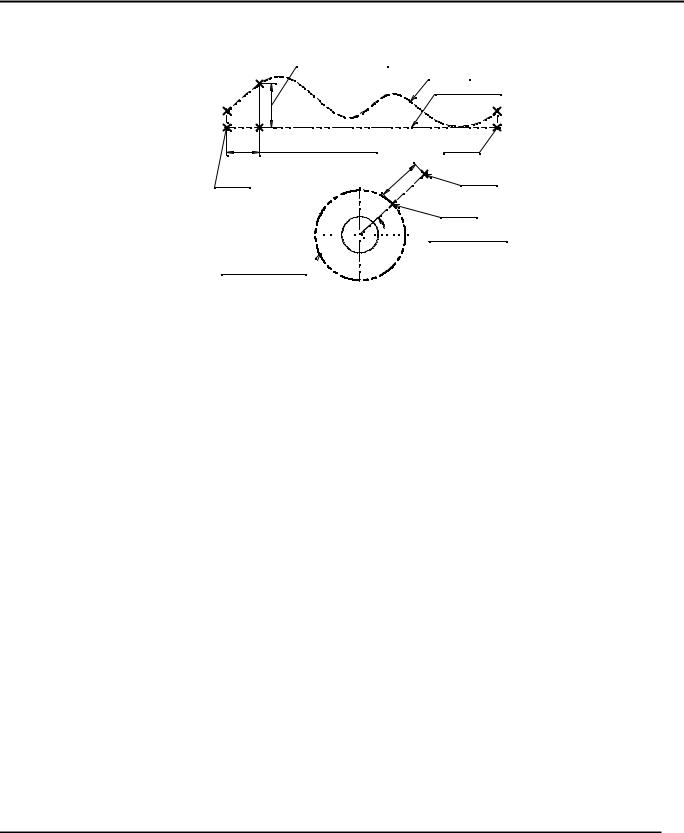
Создание 3D пути на основе сечения тела плоскостью

Для создания 3D пути необходимо указать секущую рабочую плоскость и исходное тело (операцию). По контуру пересечения тела и рабочей плоскости будет построен путь.

3D путь строится только в том случае, если в результате сечения выбранного тела плоскостью образуется один контур. Когда исходное тело твёрдое, контур будет замкнутый. При сечении листового тела получается разомкнутый контур.

Данный режим запускается с помощью опции:

<В> Создать 3D путь на основе сечения тела плоскостью

194

3D пути

В автоменю команды появляются опции для выбора секущей плоскости и тела операции:

<1> Выбрать рабочую плоскость

<2> Выбрать операцию

Создание 3D пути с параметрическим изменением 3D точки

Способ создания 3D пути с параметрическим изменением 3D точки используется для создания траекторий со сложной геометрией.

Пространственная кривая пути получается в результате «движения» 3D точки по произвольной или специально заданной пространственной траектории. «Движение» точки осуществляется за счёт многократного копирования исходной 3D точки. Полученный набор точек объединяется сплайном и формируется 3D путь. Результирующий 3D путь может быть замкнутым.

При построении такого пути используется универсальный механизм, позволяющий получать конечный результат на основе параметрического копирования исходного элемента. Этот механизм используется в операции “Тело по параметрам” – при создании тела на основе “движения” (копирования) профиля. Он же используется в операции “Параметрический массив”, где результатом выполнения операции является набор параметрически изменяющихся копий исходного объекта.

Наиболее полно работа этого алгоритма описана в главе “Тело по параметрам”. В данной главе приведено лишь краткое описание и некоторые примеры применения данного механизма.

Для создания 3D пути с параметрическим изменением точки необходимо определить закон, по которому будут строиться копии исходной 3D точки.

Для каждой копии точки рассчитывается так называемая система координат текущей копии. Копирование 3D точки осуществляется в направлении от исходной системы координат к рассчитанной целевой системе координат текущей копии. В качестве исходной системы координат пользователь может выбрать одну из локальных систем координат модели. Если локальная система координат не выбрана, то в качестве исходной системы координат используется, в зависимости от способа расчёта системы координат текущей копии, либо глобальная система координат, либо система координат первой копии.

Система координат текущей копии (т.е. её начало и ориентация осей) может определяться одним из двух способов:

•Свободная ориентация копии. Законы изменения параметров системы координат текущей копии 3D точки описываются с помощью выражений.

•Ориентация копии по 3D кривым или поверхностям. Для определения положения в пространстве системы координат текущей копии используются существующие 3D кривые или поверхности других тел. Управляя системой координат копии, пользователь управляет положением каждой копии 3D точки.

Управление системой координат копии осуществляется через параметры операции. Параметры подразделяются на два типа - управляемые параметры и управляющие параметры.

Управляемые параметры – параметры, значения которых рассчитываются автоматически в процессе создания копии точки. Для считывания значений таких параметров можно назначить независимые переменные.

195

Трёхмерное моделирование

Управляющие параметры – поля, зависимости в которых задаются пользователем. В поля управляющих переменных вписываются произвольные выражения, в которые можно включить любую переменную системы. Например, если включить в такое выражение переменную, отвечающую за номер копии 3D точки, значение данного параметра будет зависеть от номера копии.

Некоторые параметры операции могут быть как управляющими, так и управляемыми. Ведущий параметр «Номер копии» всегда является управляемым. Для него обязательно нужно выбрать независимую переменную, которой будет присваиваться текущее значение номера копии при расчёте операции. Номер копии автоматически изменяется в процессе расчёта от 1 до указанного количества с шагом 1.

Расчёт выполняется в следующем порядке: присваивается следующее значение номеру копии, рассчитываются управляющие параметры, вычисляются остальные управляемые параметры (если они есть), выполняется копирование. Все полученные копии 3D точки объединяются в один сплайн.

Пиктограмма для вызова данного режима находится в основном автоменю команды создания 3D пути:

<P> Создать путь с параметрическим изменением 3D узла

После включения режима становятся доступными следующие действия:

Как уже отмечалось выше, можно выделить два способа создания пути с параметрическим изменением 3D точки. Рассмотрим на примерах каждый из них.

Способ свободной ориентации копии

При создании пути таким способом достаточно выбрать 3D узел, задать количество копий и назначить независимую переменную на параметр “Номер копии”. Используя переменную, принимающую значения номеров копий, можно создать определённые зависимости в полях управляющих переменных, а также в 2D или 3D построениях, от которых, в свою очередь, будет зависеть положение исходной 3D точки.

Пример 1

Рассмотрим применение параметрического пути на примере создания модели кулачка. Данный пример находится в библиотеке “Примеры для документации”, в папке “Трехмерное

196

3D пути

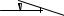
моделирование/3D Пути/Кулачок.grb” Исходными данными является график, задающий поверхность кулачка.

Узел 3

Угол задаётся переменной "а1"

"Свёрнутая" ось графика

Между узлами 1 и 2 построена пропорциональная прямая. Её положение определяется значением переменной “а” в пределах от 0 до 1 включительно. При изменении значения переменной “а” прямая будет двигаться от точки 1 к точке 2. Полученная прямая пересекает ось графика и кривую графика. Между этими точками можно построить отрезок. Его длина будет равна текущему значению функции графика. Считанное (с помощью функции get) значение длины отрезка хранит переменная

“L”.

Для построения 3D пути, повторяющего контур поверхности кулачка, необходимо создать такой 3D узел, который бы при изменении одной переменной (назначенной на счётчик копий) изменял своё пространственное положение в соответствии с заданным законом на графике. Такой узел удобно создать, если добавить ещё несколько 2D построений с использованием уже полученных данных.

Для того чтобы получился кулачок нужных размеров, ось графика должна быть “свёрнута” в окружность заданного радиуса. В данном примере построена окружность радиусом 50 мм. Через центр окружности под углом к горизонтали нужно построить новую прямую. На параметр, задающий угол наклона этой прямой, нужно назначить переменную “а1”.

На пересечении окружности и наклонной прямой построен узел 3. Относительно узла 3, вдоль наклонной прямой построен узел 4 на расстоянии “L”. По 2D узлу 4 построен 3D узел. Для этого на существующей странице предварительно создана рабочая плоскость “Вид спереди”.

Теперь нужно связать все переменные между собой таким образом, чтобы при изменении счетчика копий перестраивался 3D узел. Этого можно добиться, если вместо конкретных значений некоторых переменных ввести следующие выражения, задающие зависимость от номера копий:

197

Трёхмерное моделирование

Поскольку значения параметра “Номер копии” всегда начинаются с единицы, иногда требуется вводить поправку (–1) в выражения, где участвует переменная “Номер копии”.

Теперь можно строить параметрический 3D путь. В диалоге параметров нужно определить два параметра: задать количество копий, и назначить переменную, которая будет выполнять функцию счётчика копий. В данном примере на параметр “Номер копии” назначена переменная “s”.

Первая копия 3D узла будет совпадать по положению со 101-й. В результате получится замкнутый 3D путь. Его геометрия будет соответствовать форме кулачка.

Далее для получения тела кулачка нужно вытолкнуть путь по нормали на 50 единиц и на основе получившейся листовой поверхности создать твёрдое тело с помощью операции “Сшивка”.

В завершение можно сделать цилиндрическое отверстие по оси кулачка (выталкивание окружности с автоматическим вычитанием из основного тела).

Способ ориентации копии по путям или поверхностям

Способ ориентации копии по путям или поверхностям удобно использовать, когда не удаётся точно описать закон изменения параметров копии с помощью выражений. В таких случаях бывает удобно использовать различные 3D кривые или поверхности для определения положения и ориентации системы координат текущей копии.

198

3D пути

Пример 2

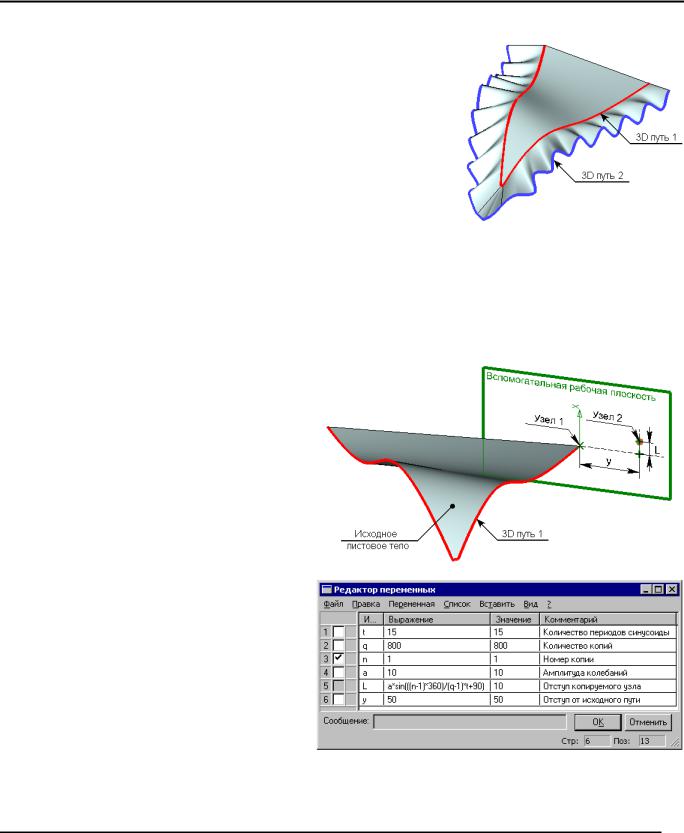
В качестве примера применения параметрического 3D пути с ориентацией копии по путям или поверхностям можно рассмотреть построение 3D пути, определяющего внешний край “волнистой” поверхности. На рисунке он обозначен как

3D путь 2.

Для построения такого пути необходимы:

-исходный 3D узел, положение которого должно меняться при создании пути в зависимости от номера создаваемой копии;

-3D путь, определяющий положение начала системы координат каждой копии;

-поверхность, определяющая ориентацию оси X системы координат каждой копии.

Создаваемый путь должен повторять форму внешнего края исходного листового тела. Поэтому для задания начала системы координат копий необходимо использовать 3D путь, построенный по рёбрам исходного листового тела – 3D путь 1.

Для получения исходного 3D узла построена вспомогательная рабочая плоскость, перпендикулярная 3D пути 1 и проходящая через одну из вершин исходного листового тела.

На рабочей плоскости созданы необходимые 2D построения. Искомый 3D узел создан по 2D узлу на рабочей плоскости – Узлу 2.

Узел 2 был построен следующим образом: на рабочей плоскости построен Узел 1 с координатами (0,0) (соответствует той вершине исходного листового тела, через которую проходит рабочая плоскость). Через данный узел проведена горизонтальная прямая. Перпендикулярно горизонтальной прямой, на расстоянии “y” от Узла 1, проведена вертикальная прямая. Узел 2 лежит на данной прямой на расстоянии “L” от точки пересечения прямых.

Значение переменной “L” задано так, чтобы оно менялось при изменении счётчика копий 3D пути. Таким образом, при построении 3D пути, в зависимости от номера текущей копии по синусоидальному закону меняется положение 2D Узла 2 и построенного на его основе 3D узла.

199