
- •ОСНОВНЫЕ ПРИНЦИПЫ И ПОНЯТИЯ 3D МОДЕЛИРОВАНИЯ В T-FLEX CAD 3D
- •Введение в 3D моделирование
- •Основные топологические элементы
- •Основные геометрические понятия в системе T-FLEX CAD 3D
- •Элементы и операции в 3D
- •3D элементы построения
- •Основные трёхмерные операции
- •Операции для работы с листовым металлом
- •Операции для работы с гранями
- •Операции по вставке и копированию 3D элементов
- •Операции создания 3D массивов
- •Команды для анализа геометрии
- •Вспомогательные команды и операции
- •2D проекции
- •Визуализация трёхмерных объектов
- •Анимация трёхмерной модели
- •Организация твердотельного моделирования в T-FLEX CAD 3D
- •Общие рекомендации перед созданием 3D модели
- •Параметризация. Регенерация модели
- •Методы создания трёхмерной модели
- •Как работать в системе T-FLEX CAD 3D
- •Получение справки
- •Создание нового документа. Использование шаблона-прототипа
- •Работа мышкой. Контекстное меню
- •Ввод команд (с клавиатуры, с помощью пиктограмм, из текстового меню)
- •Задание параметров создаваемого элемента
- •Предварительный просмотр
- •Команды T-FLEX CAD 3D по группам
- •Выбор элементов. Настройка
- •Выбор элементов
- •Поиск элементов
- •Открытие новых окон
- •Манипулирование моделью в 3D окне
- •Окно «3D модель»
- •Окно «Диагностика»
- •Оптимальное расположение служебных окон
- •Панели инструментов
- •Настройки
- •КРАТКИЙ ВВОДНЫЙ КУРС ПО СОЗДАНИЮ 3D МОДЕЛИ
- •Основной метод создания 3D модели
- •Создание вспомогательных элементов
- •Создание первой операции вращения
- •Создание отверстий
- •Создание сглаживания
- •Создание чертежа
- •Метод «От чертежа к 3D модели»
- •РАБОТА С ОКНОМ 3D ВИДА
- •Основные положения
- •Методы визуализации 3D сцены
- •3D сцена
- •Активная камера
- •Вращение 3D сцены
- •Автоматическое вращение 3D сцены
- •Центр вращения 3D сцены
- •Метод проецирования
- •Автомасштабирование
- •Плоскость обрезки
- •Параметры 3D вида
- •Вызов команд управления 3D видом с помощью мыши
- •ОБЩИЕ ПАРАМЕТРЫ 3D ЭЛЕМЕНТОВ
- •Общесистемные параметры
- •Закладка «Общие»
- •Закладка «Преобразование»
- •РАБОЧИЕ ПЛОСКОСТИ
- •Начало работы с рабочими плоскостями
- •Рабочие плоскости и 2D чертёж
- •Работа с активной рабочей плоскостью
- •Активизация рабочей плоскости
- •Управление активной рабочей плоскостью
- •Создание рабочих плоскостей
- •Создание рабочей плоскости параллельно геометрической плоскости
- •Создание рабочей плоскости, проходящей через 3D точку
- •Создание рабочей плоскости, проходящей через 3D линию
- •Создание рабочей плоскости, перпендикулярной 3D кривой
- •Создание рабочей плоскости, касательной к поверхности
- •Выбор начала координат рабочей плоскости
- •Создание копии рабочей плоскости
- •Создание рабочей плоскости на основе локальной системы координат
- •Создание стандартной рабочей плоскости (в 3D окне)
- •Создание стандартной рабочей плоскости (в 2D окне)
- •Создание рабочей плоскости на основе 2D проекции
- •Создание рабочей плоскости для вспомогательного 2D вида
- •Изменение размера рабочей плоскости
- •Параметры рабочих плоскостей
- •Закладка «Рабочая плоскость»
- •РАБОЧИЕ ПОВЕРХНОСТИ
- •Основные положения
- •Этапы создания рабочей поверхности
- •Параметрическая область
- •Фиксированный параметр рабочей поверхности
- •Система координат, относительно которой задаётся рабочая поверхность
- •Пример использования рабочей поверхности
- •Правила создания рабочих поверхностей
- •3D УЗЛЫ
- •Способы создания узлов
- •Использование манипулятора при создании 3D узла
- •Основные способы создания узла на 3D элементе или относительно 3D элемента
- •Специальные способы создания узла на основе существующих 3D элементов
- •Создание узла в абсолютных координатах
- •Создание узла по двум проекциям
- •3D ПРОФИЛИ
- •Основные положения. Типы профилей
- •Геометрия профиля
- •Типы профилей
- •Профили на основе 2D элементов
- •Профиль на основе штриховки
- •Профиль на основе текста
- •Профиль на основе линий изображения на рабочей плоскости
- •Автоматическое создание профилей на основе 2D элементов (на активной рабочей плоскости)
- •Профили на основе 3D элементов
- •Профиль на основе цикла или грани
- •Проецирование профиля на грань или тело
- •Копирование 3D профиля
- •3D профиль - эквидистанта
- •Наложение профиля на грань или тело
- •Построение развёртки линейчатой грани
- •Построение развёртки цилиндрической грани
- •Построение развёртки конической грани
- •Построение развёртки набора граней
- •Придание толщины плоскому профилю
- •Создание 3D профилей
- •Создание 3D профиля на основе 2D штриховки или текста
- •Создание 3D профиля на основе линий изображения на рабочей плоскости
- •Автоматическое создание профилей при работе с активной рабочей плоскостью
- •Создание 3D профиля на основе цикла или грани
- •Создание профиля - проекции существующего профиля на грань или тело
- •Копирование 3D профиля
- •Создание 3D профиля - эквидистанты
- •Наложение профиля на грань или тело
- •Придание толщины плоскому профилю
- •Параметры 3D профилей
- •ЛОКАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ
- •Правила создания локальных систем координат
- •Определение начала координат ЛСК
- •Определение направления оси X ЛСК
- •Определение направления оси Y ЛСК
- •Доворот оси X ЛСК до ближайшей точки выбранной поверхности
- •Перемещение ЛСК до касания с поверхностью
- •Изменение ориентации осей локальной системы координат
- •Создание локальных систем координат
- •Параметры локальных систем координат
- •3D ПУТИ
- •Способы создания 3D путей
- •Создание 3D путей на основе 3D элементов
- •Создание 3D пути как сплайна по 3D точкам
- •3D путь по связанным рёбрам
- •3D путь по последовательности 3D путей
- •3D путь как проекция 3D пути на грань или тело операции
- •Создание копии 3D пути
- •3D путь как линия очерка
- •Создание эквидистанты к 3D пути
- •Создание 3D пути на основе сечения тела плоскостью
- •Создание 3D пути с параметрическим изменением 3D точки
- •3D пути на основе 2D элементов
- •Создание 3D пути на основе контура штриховки
- •Создание 3D пути по 2D путям
- •Создать 3D путь по двум проекциям
- •ПУТЬ ТРУБОПРОВОДА
- •Создание 3D пути для трубопровода
- •Плоскость черчения
- •СЕЧЕНИЕ
- •Основные способы создания 3D сечений
- •3D сечение на основе 3D вида
- •3D сечение на основе рабочей плоскости
- •Создание 3D сечения на основе 2D проекции
- •Применение сечения к 3D модели
- •Создание сечения
- •Создание сечения по 3D виду
- •Создание сечений на основе рабочей плоскости
- •Создание сечения на основе 2D проекции
- •Задание параметров 3D сечения
- •2D ПРОЕКЦИИ
- •Создание 2D проекции
- •Построение стандартных видов
- •Создание дополнительного вида
- •Создание разреза или сечения
- •Создание местного разреза
- •Построение проекции на рабочей плоскости
- •Общий случай создания 2D проекции
- •Выбор элементов для проецирования
- •Создание разрыва на проекции
- •Особенности построения и дальнейшее использование 2D проекций
- •Параметры 2D проекции
- •Закладка «Общие»
- •Закладка «Основные параметры»
- •Закладка «Линии»
- •Редактирование 2D проекции
- •ВЫТАЛКИВАНИЕ
- •Основные понятия. Возможности операции
- •Контур выталкивания
- •Направление выталкивания
- •Задание длины выталкивания
- •Типы границ
- •Дополнительные возможности выталкивания
- •Создание операции выталкивания
- •Выбор контура выталкивания
- •Задание направления выталкивания
- •Задание длины выталкивания
- •Задание дополнительных возможностей операции
- •ВРАЩЕНИЕ
- •Основные понятия. Возможности операции
- •Контур вращения
- •Ось вращения
- •Угол вращения контура
- •Дополнительные возможности операции вращения
- •Создание операции вращения
- •Выбор контура вращения
- •Задание оси вращения
- •Задание начального угла и угла поворота
- •БУЛЕВА ОПЕРАЦИЯ
- •Основные понятия. Возможности операции
- •Типы булевой операции
- •Операнды булевой операции
- •Результаты булевых операций
- •Глобальные и локальные булевы операции
- •Выборочные булевы операции
- •Создание булевой операции
- •Основные параметры операции
- •Дополнительные параметры операции
- •СГЛАЖИВАНИЕ РЁБЕР
- •Основные понятия. Возможности операции
- •Виды сглаживания
- •Особенности сглаживания группы рёбер
- •Специальные функции сглаживания рёбер
- •Правила задания операции
- •Правила выбора объектов
- •Задание параметров операции. Использование манипуляторов
- •СГЛАЖИВАНИЕ ГРАНЕЙ
- •Основные понятия. Возможности операции
- •Направляющая
- •Типы сглаживания
- •Режимы сглаживания
- •Формы поверхности сглаживания
- •Специальные возможности
- •Граничные условия
- •Правила задания операции
- •Работа с манипуляторами и декорациями
- •Выбор набора граней
- •Выбор режима сглаживания
- •Выбор типа сглаживания
- •Задание формы поперечного сечения
- •Задание граничных условий
- •Настройка специальных возможностей
- •СГЛАЖИВАНИЕ ТРЁХ ГРАНЕЙ
- •Основные понятия. Возможности операции
- •Общие концепции операции
- •Дополнительные возможности
- •Правила задания операции
- •Выбор набора граней
- •Выбор направляющей
- •Настройка специальных возможностей
- •ПО СЕЧЕНИЯМ
- •Основные понятия. Возможности операции
- •Сечения
- •Точки соответствия
- •Направляющие
- •Граничные условия
- •Совместимость со старыми версиями
- •Правила задания операции «По сечениям»
- •Выбор сечений
- •Задание точек соответствия
- •Выбор направляющих
- •Задание граничных условий
- •Задание дополнительных параметров операции
- •Параметры сглаживания
- •Параметры оптимизации
- •ТЕЛО ПО ТРАЕКТОРИИ
- •Основные возможности операции
- •Контур
- •Контроль над ориентацией контура
- •Траектория и направляющие
- •Коррекция исходного положения контура
- •Кручение контура
- •Масштабирование контура
- •Создание тела по направляющим
- •Методы вычисления вспомогательных векторов с использованием направляющих
- •Правила задания операции
- •Выбор способа ориентации контура
- •Выбор контура
- •Выбор траектории
- •Задание коррекция исходного положения контура
- •Задание закона кручения контура
- •Задание закона масштабирования контура
- •Задание тела по направляющим
- •Дополнительные возможности операции
- •ТЕЛО ПО ПАРАМЕТРАМ
- •Правила создания операции
- •Способ свободной ориентации копии
- •Пример 1
- •Пример 2
- •Способ ориентации копии по путям или поверхностям
- •Пример 3
- •ТРУБОПРОВОД
- •Задание операции трубопровод
- •3D ИЗОБРАЖЕНИЯ
- •Создание 3D изображений
- •Использование 3D изображений для создания планировок
- •Параметры 3D изображений
- •Закладка «Операция»
- •Закладка «Преобразование»
- •ВНЕШНЯЯ МОДЕЛЬ
- •Режимы работы с внешней моделью
- •Вставка внешней модели
- •3D КОПИИ
- •Основные положения и возможности операции
- •Выбор исходного тела (операции)
- •Исходная и целевая системы координат
- •Способы копирования
- •Создание копии
- •Выбор 3D операции
- •Выбор исходной системы координат
- •Выбор целевой системы координат
- •Задание параметров операции
- •Подтверждение создания копии
- •МАССИВЫ
- •Типы массивов. Особенности каждого типа
- •Массив элементов построения
- •Массив Тел и массив операций
- •Массив граней
- •Виды массивов. Особенности массивов каждого вида
- •Линейный массив
- •Круговой массив
- •Массив по точкам
- •Массив по пути
- •Параметрический массив
- •Ограничения и исключения
- •Ограничения
- •Исключения
- •Изменение числа копий в массиве. Привязка к элементам массива
- •Создание 3D массивов
- •Выбор типа массива и исходных объектов массива
- •Задание направляющих элементов и основных параметров массива
- •Задание дополнительных параметров массива
- •Задание ограничений
- •Задание исключений
- •3D СИММЕТРИЯ
- •Создание симметричного тела
- •ОТСЕЧЕНИЕ
- •Задание операции отсечения
- •Создание отсечения
- •Создание рассечения
- •Примеры создания операции
- •Рассечение тела на две части
- •РАЗДЕЛЕНИЕ
- •Создание разделения
- •Параметры разделения
- •УКЛОН ГРАНЕЙ
- •Основные понятия и возможности операции
- •Направление уклона
- •Неподвижное ребро
- •Отсчёт угла уклона
- •Неподвижная грань
- •Использование рабочей плоскости
- •Уклон всех смежных граней
- •Совместная обработка граней
- •Методы уклона граней
- •Уклон граней по смещению
- •Использование нескольких неподвижных граней/ребер
- •Обработка стыка между уклоняемой и смежной с ней гранями
- •Обработка стыка между двумя уклоняемыми гранями
- •Ступенчатый уклон
- •Разбиение грани
- •Создание уклона граней
- •Основные параметры операции
- •Дополнительные параметры операции
- •УКЛОН ТЕЛА
- •Основные понятия и возможности операции
- •Направление уклона
- •Исходные ребра
- •Разделяющее тело
- •Исходные грани
- •Угловое соединение
- •Исправление вогнутых углов
- •Обработка стыков уклоненных граней
- •Подрез уклона
- •Замена ребер
- •Создание уклона тела
- •Основные исходные данные операции
- •Дополнительные параметры операции
- •ОБОЛОЧКА
- •Основные положения
- •Создание оболочки
- •Выбор удаляемой грани или тела
- •Выбор граней, для которых толщина стенки задается отдельно
- •Дополнительные параметры операции
- •ПРУЖИНЫ
- •Основные сведения и возможности операции
- •Создание операции пружина
- •Задание оси пружины
- •Задание параметров операции пружина
- •Выбор стартовой точки положения профиля пружины
- •Задание поджима и зашлифовки концов пружины
- •Задание выравнивания пружины по начальной и конечной точкам
- •СПИРАЛИ
- •Основные сведения и возможности операции
- •Ось спирали
- •Профиль спирали и его ориентация в пространстве
- •Основные параметры спирали
- •Начальное положение профиля спирали
- •Сглаживание
- •Задание операции спираль
- •Задание оси спирали
- •Выбор профиля спирали
- •Задание ориентации 3D профиля в пространстве
- •Задание параметров спирали
- •Выбор стартовой точки положения профиля спирали
- •РЕЗЬБА
- •Основные понятия. Возможности операции
- •Создание резьбы
- •Задание основных параметров резьбы
- •Задание отступов
- •Отображение резьбы на 2D проекциях
- •Резьбовые соединения
- •ОТВЕРСТИЯ
- •Основные понятия и возможности операции
- •Шаблоны отверстий
- •Точки привязки отверстий
- •Соосные отверстия
- •Ориентация отверстий
- •Глубина отверстия
- •Отверстия через несколько тел
- •Создание отверстий
- •Выбор типа и основных геометрических параметров отверстий
- •Задание точек привязки отверстий
- •Задание глубины отверстия
- •Создание отверстий через несколько тел одновременно
- •Выбор отверстия для изменения положения и ориентации отверстия
- •Изменение точки привязки отверстия
- •Изменение ориентации отверстия. Создание соосного отверстия
- •РАБОТА С ЛИСТОВЫМ МЕТАЛЛОМ
- •Подготовительные операции при работе с листовым металлом
- •Общие параметры листового металла
- •Заготовка для листовых операций
- •Гибка. Основные понятия и возможности
- •Виды гибки
- •Общие параметры гибки
- •Основные понятия гибки
- •Сгибание
- •Отгибание
- •Приклеивание
- •Уменьшение язычка
- •Ослабления напряжений в металле
- •Дополнительные операции при работе с листовым металлом
- •Разгибание детали
- •Повторная гибка развёрнутой заготовки
- •Библиотека часто встречающихся элементов штамповки
- •Правила задания операций листовой штамповки
- •Задание параметров листовых операций
- •Создание заготовки
- •Создание различных видов гибки
- •Разгибание
- •Повторная гибка
- •Создание типовых операций листовой штамповки
- •ОПЕРАЦИИ ДЛЯ РАБОТЫ С ГРАНЯМИ
- •Сшивка
- •Работа с командой
- •Выбор сшиваемых поверхностей
- •Задание дополнительных параметров
- •Разделение граней
- •Работа с командой
- •Выбор метода разделения
- •Выбор разделяемых объектов
- •Выбор разделяющих объектов
- •Задание направления
- •Удаление граней
- •Основные положения
- •Работа с командой
- •Выбор удаляемых граней
- •Выбор способа удаления
- •Дополнительные параметры
- •Отделение граней
- •Основные положения
- •Работа с командой
- •Выбор отделяемых граней
- •Указание методов обработки исходных и отделяемых граней
- •Замена граней
- •Основные положения
- •Работа с командой
- •Выбор заменяемых и заменяющих граней
- •Задание дополнительных параметров
- •Изменение граней
- •Основные положения
- •Работа с командой
- •Выбор изменяемых граней
- •Указание параметров граней
- •Задание дополнительных параметров
- •Перемещение граней
- •Работа с командой
- •Задание перемещаемых граней
- •Задание параметров преобразования
- •Расширение поверхности
- •Работа с командой
- •Выбор расширяемого объекта
- •Выбор рёбер
- •Задание величины продления грани
- •Задание дополнительных параметров
- •Заполнение области
- •Работа с командой
- •Выбор области заполнения
- •Выбор листового тела
- •Задание дополнительных параметров
- •3D СБОРКИ
- •Общие сведения
- •Что такое трехмерная сборочная модель?
- •Методы проектирования сборок
- •Создание сборки из 3D фрагментов
- •Принцип работы механизма 3D фрагментов
- •Правила работы с 3D фрагментами
- •Подготовка документа T-FLEX CAD к использованию в качестве 3D фрагмента.
- •Проектирование сборок «Сверху вниз»
- •Принцип работы
- •Правила создания Детали
- •Сопряжения и степени свободы
- •Что такое сопряжение?
- •Типы сопряжений
- •Создание сопряжений
- •Приёмы работы с готовыми сопряжениями
- •Конфигурации
- •Что такое Конфигурация?
- •Работа с Конфигурациями
- •Деталировка
- •Разборка
- •Выполнение команды
- •Как правильно задать преобразования для разборки
- •АДАПТИВНЫЕ 3D ФРАГМЕНТЫ
- •Подготовка адаптивного 3D фрагмента
- •Вставка адаптивного 3D фрагмента, задание значений адаптивных элементов
- •Задание адаптивных элементов у существующего фрагмента
- •РЕДАКТИРОВАНИЕ 3D ЭЛЕМЕНТОВ
- •ПРЕОБРАЗОВАНИЕ
- •Типы преобразований
- •Перемещение/поворот
- •Поворот вокруг оси
- •Перемещение вдоль вектора
- •Масштабирование
- •Симметрия
- •Преобразование 3D фрагмента
- •Преобразование сопряжения
- •Работа с командой
- •Использование манипуляторов
- •Дополнительные опции и параметры
- •МАТЕРИАЛЫ
- •Создание и редактирование материалов
- •Группа «Цвета»
- •Группа «Текстура»
- •Группа «Отображение текстуры»
- •Группа «Преобразование текстуры»
- •Группа «Штриховка в сечении»
- •Материал POV-Ray
- •Дополнительные параметры
- •Нанесение материала на отдельную грань (грани)
- •ИСТОЧНИКИ СВЕТА
- •Создание источника света
- •Точечный источник света
- •Направленный источник света
- •Прожектор
- •Параметры источника света
- •КАМЕРЫ
- •Создание камер
- •Задание камеры
- •Активация камеры
- •Перемещение камеры
- •Параметры камеры
- •ФОТОРЕАЛИСТИЧНОЕ ИЗОБРАЖЕНИЕ
- •Основные положения
- •Работа с командой
- •Прототипы для фотореализма
- •Выбор и настройка качества изображения
- •Примеры фотореалистичных изображений моделей T-FLEX CAD
- •АНАЛИЗ ГЕОМЕТРИИ
- •Характеристики
- •Работа с командой
- •Проверка модели
- •Работа с командой
- •Проверка пересечений тел
- •Работа с командой
- •Измерение кривизны кривых
- •Измерение кривизны поверхностей
- •Работа с командой
- •Типы измеряемых величин
- •Измерение кривизны в точке
- •Отклонение граней
- •Работа с командой
- •Зазор между гранями
- •Работа с командой
- •Расхождение нормалей
- •Работа с командой
- •Гладкость модели
- •Работа с командой
- •Разнимаемость формы
- •Работа с командой
Рабочие поверхности
РАБОЧИЕ ПОВЕРХНОСТИ
Рабочие поверхности – это вспомогательные 3D элементы, представляющие собой образ геометрической поверхности определённого типа. В качестве таких поверхностей могут использоваться цилиндр, сфера и тор. По функциональному назначению рабочие поверхности схожи с рабочими плоскостями. В основном они предназначены для переноса 2D объектов чертежа в 3D пространство. Каждая рабочая поверхность всегда связана с параметрической областью, расположенной на странице 2D чертежа. На основе плоского 2D изображения, лежащего на данной странице, можно создать вспомогательные 3D элементы (3D узлы, 3D профили, 3D пути), которые будут лежать на соответствующей рабочей поверхности – цилиндре, сфере или торе.
Основное назначение рабочих поверхностей - построение вспомогательных объектов (3D профилей) для создания деталей с поверхностями двойной кривизны: лопаток турбин, гребных винтов, корпусов кораблей, фюзеляжей летательных аппаратов.
Основные положения
Рабочие поверхности определяются с помощью специальных параметрических систем координат:
-цилиндрической;
-сферической;
-тороидальной.
Отсчёт параметрических координат (их смысл и диапазон зависят от типа поверхности) всегда ведётся относительно ортогональной (декартовой) системы координат. В качестве таковой может
125
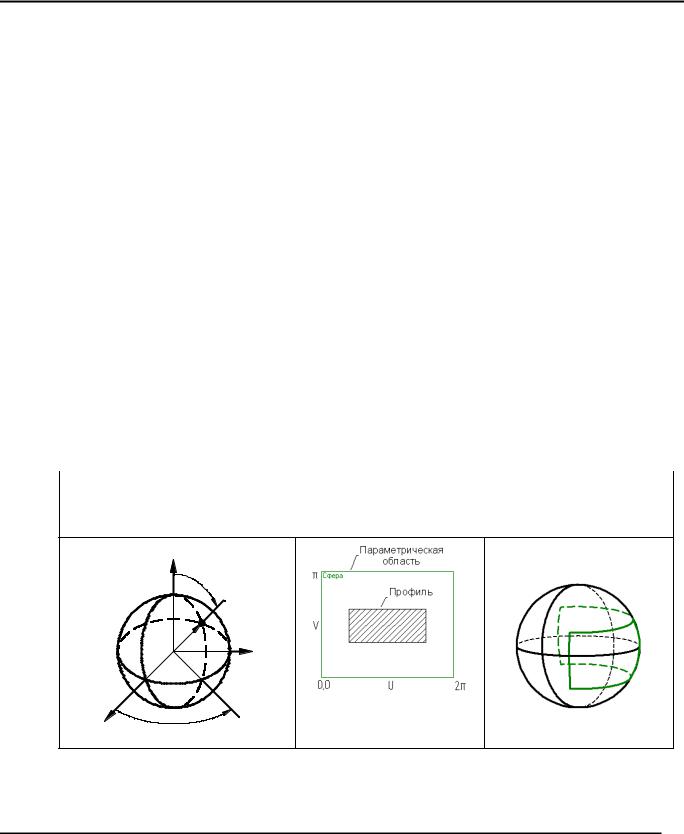
Трёхмерное моделирование
использоваться как мировая система координат, так и специально выбранная локальная система координат (ЛСК).
Вцилиндрической системе координат положение точки определяется тремя параметрами – величиной радиуса цилиндра, смещением вдоль оси цилиндра (оси Z) и углом (или длиной дуги) между осью X и проекцией радиус-вектора точки на плоскость XY.
Всферической системе координат положение точки определяется тремя параметрами – величиной радиуса сферы, углом между осью X и проекцией радиус-вектора точки на плоскость XY, углом между радиус-вектором и осью Z.
Второидальной системе координат положение точки определяется четырьмя параметрами – двумя определяющими радиусами тора, углом между осью X и проекцией радиус-вектора на плоскость XY, углом в плоскости Z-радиус-вектор.
Параметры, задающие радиус цилиндра, сферы, два радиуса тора являются фиксированными, т.е. совпадают у точек, принадлежащих одной и той же поверхности. Это константная характеристика данной поверхности. У цилиндра и сферы – один фиксированный параметр-радиус, у тора – два (два радиуса тора).
Таким образом, положение точки поверхности любого типа в специальной системе координат фактически определяется двумя параметрическими ортогональными координатами (U и V). Благодаря этому любую из специальных систем координат можно связать с прямоугольной областью на плоскости (параметрической 2D областью). 2D область будет представлять собой “развертку” поверхности на плоскость (согласно формулам преобразования UV-координат в декартовы координаты для выбранного типа поверхности), играя ту же роль, что и изображение рабочей плоскости на странице 2D чертежа. Кроме того, 2D область будет определять диапазон изменения UV-координат.
Введение параметрической 2D области позволяет работать с поверхностью как с обычной рабочей плоскостью.
Графическая |
Параметрическая 2D |
Профиль в 3D |
|
Иллюстрация |
область |
||
|
|||
|
|
|
Сферическая система координат
Z |
|
v |
|
R |
Y |
|
|
X
u
U – угол от оси X (0-2π) V – угол от оси Z (0-π) R – радиус сферы
126
