Модуль 4.3. Метод сигнальных графов

Цель модуля: Знакомство с основами метода сигнальных графов и его приме нения для анализа цепей

Общие сведения

Решение уравнений электрического равновесия сложных цепей даже прибли женными численными методами, как правило, является весьма трудоемким. Задача анализа цепи становится особенно сложной в случае, когда неизвестные токи и на пряжения или комплексные частотные характеристики должны быть найдены в ви де аналитических соотношений. При этом полезным может оказаться применение метода сигнальных графов, который позволяет упростить решение уравнений элек трического равновесия линейных электрических цепей в аналитическом виде (сим вольной форме).

Как отмечалось в модуле 1.4, сигнальный граф или направленный граф прохождения сигналов, представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. Узлы (верши­ ны) такого графа соответствуют входящим в эту систему неизвестным величинам (токам и напряжениям ветвей, контурным токам, узловым напряжениям) и величи нам, характеризующим внешние воздействия на цепь (токам независимых источни ков тока, ЭДС независимых источников напряжения, контурным ЭДС, узловым то кам). Ветви сигнального графа отображают причинно следственные связи между величинами, соответствующими отдельным узлам. В рамках метода сигнальных графов эти величины называются сигналами. Каждой ветви сигнального графа приписывается определенное направление и присваивается весовой коэффициент, который называется передачей ветви. Узлы сигнального графа обозначают теми же буквами, что и соответствующие узлам величины; направления ветвей показы вают стрелками, около которых указывают передачу ветви.

Рис. 4.20. Сигнальные графы, соответствующие выражениям (4.30) и (4.31)

Если ветвь с передачей А направлена от узла хi к узлу хj (рис. 4.20, а), то

. 4.30

Следовательно, при прохождении через ветвь сигнал умножается на передачу ветви. Разрешим уравнение (4.30) относительно хi

. 4.31

375

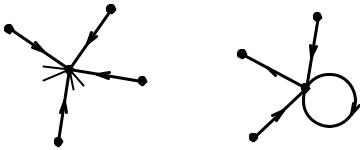
Сигнальный граф, соответствующий этому уравнению (рис. 4.20, б), отличается от сигнального графа, соответствующего уравнению (4.30), направлением и передачей ветви. Таким образом, вид сигнального графа зависит от того, относительно какой из величин разрешено заданное уравнение, т. е. от того, какая из величин рассмат ривается как причина, а какая — как следствие.

Если в узле хk сходится несколько ветвей (рис. 4.21, а), то значение сигнала в этом узле равно сумме сигналов всех входящих в него ветвей:

где N — число ветвей, направленных к узлу хk; Aki — передача ветви, направленной от узла хi к узлу хk. Ветви, направленные от узла хk, не влияют на его сигнал и при подсчете хk не учитываются. В число ветвей, направленных к исследуемому узлу, мо гут входить и ветви, начинающиеся в данном узле (рис. 4.21, б). Такие ветви назы ваются петлями. Значение переменной в узле, к которому подключена одна или не сколько петель, находится по общему правилу (4.32), например, для рис. 4.21, б,

. 4.33

Из выражения (4.33) следует, что при наличии петель, подключенных к како му либо узлу, переменная, соответствующая этому узлу, входит и в левую, и в пра вую части уравнения (4.32).

Рис. 4 21. Суммирование сигналов в узле сигнального графа

Рассмотрим некоторые понятия, относящиеся к сигнальным графам.

Истоком называется узел сигнального графа, от которого направлены все примыкающие к нему ветви. Узел сигнального графа, к которому направлены все примыкающие к нему ветви, называется стоком. Узлы, которые имеют как входя щие, так и исходящие ветви, называются смешанными. Например в графе рис.4.20, а узел xi — исток, узел xj — сток; в графе рис. 4.21, б узлы х1, и х2 истоки, узел х3 – сток, узел х4 — смешанный.

376

Два контура или контур и путь называются соприкасающимися, если они имеют, общие узлы. Если два контура или контур и путь не имеют общих узлов, то они являются несоприкасающимися. На рис. 4.22 контуры с передачами L2= gc и L4 = f, L3= a и L4= f несоприкасающиеся, а контуры с передачами L1= be и L2= gc; L1= be и L4 = f; L1 = be и L3= a — соприкасающиеся. Контур с передачей L4= f не соприкасается

Как видно из примера 4.16, каждому сигнальному графу можно однозначным образом поставить в соответствие систему линейных алгебраических уравнений со ставленных относительно сигналов зависимых узлов. Для решения обратной задачи

— построения сигнального графа, соответствующего заданной системе уравнений, эта система уравнений должна быть приведена к причинно следственной форме, т. е. каждое из входящих в систему уравнений должно быть разрешено относительно одной из переменных (различных для каждого из уравнений). Далее определяется общее число узлов графа N, которое равно сумме числа неизвестных переменных и числа ненулевых свободных членов входящих в систему уравнений. Построение сигнального графа начинается с нанесения точек, соответствующих его узлам. Затем узлы графа в соответствии с системой уравнений, приведенной к причинно следственной форме, соединяются между собой ветвями так, чтобы сумма сигналов всех ветвей, сходящихся в каждом узле, равнялась бы сигналу этого узла. Для повы шения наглядности изображения рекомендуется располагать истоки в левой части чертежа, стоки в правой, а остальные узлы — между ними.

В связи с тем, что одну и ту же систему уравнений можно различными способа ми привести к причинно следственной форме, каждой системе уравнений можно по ставить в соответствие некоторое множество графов. Различные графы, соответст вующие одной и той же исходной системе уравнений, называются равносильными.

Рассмотрим несколько примеров построения графов, соответствующих задан ной системе уравнений.

Пример4.17. Построим сигнальный граф, соответствующий системе уравнений

;

;

0.

Приведем данную систему уравнений к причинно следственной форме, для чего разрешим первое уравнение относительно x1, второе – относительно x2 , а третье – относи тельно x3 :

;

;

.

Число независимых переменных в этой системе уравнений равно трем, число нену левых свободных членов — двум, следовательно, общее число узлов сигнального графа рав но пяти. Располагая в левой части чертежа независимые узлы, соответствующие свободным

378

членам b1, и b2, а в правой части узлы, соответствующие неизвестным величинам x1, х2, х3, и соединяя их ветвями в соответствии с системой уравнений, преобразованной к причинно следственной форме, получаем сигнальный граф, изображенный на рис. 4.23, а.

Рис. 4.23. К примеру 4.17

Исходная система уравнений может быть приведена к причинно следственной форме и другим способом. Прибавляя к правой и левой частям первого уравнения х1, второ го х2, третьего х3 и выполняя очевидные преобразования, находим

1;

1 ;

1 .

Этой системе уравнений соответствует сигнальный граф, изображенный на рис.4.23, б.

Графы рис. 4.23, а, б имеют различную структуру и передачи ветвей, однако они соответствуют одной и той же исходной системе уравнений и поэтому являются равно сильными. Очевидно, что если первое уравнение, входящее в исходную систему, разрешить не относительно х1, а относительно х2 или х3, то получатся другие варианты представления исходной системы уравнений в причинно следственной форме, каждому из которых можно поставить в соответствие сигнальные графы, равносильные графам, изображенным на рис. 4.23.

Пример4.18. Составим сигнальный граф, соответствующий узловым уравнениям цепи, схема которой приведена на рис. 4.2, а.

Узловые уравнения данной цепи были составлены при рассмотрении примера 4.5. Разрешая первое из этих уравнений относительно 30, а второе— относительно 20, получа ем

Этой системе уравнений соответствует сигнальный граф, приведенный на рис. 4.24.

Рис. 4.24. К примеру 4.18

379