Модуль 4.2. Основные теоремы теории цепей

Цель модуля: изучение основных теорем теории цепей и их применение для анализа цепей.

Принцип наложения

Сформулированный в гл. 1 принцип наложения (суперпозиции) отражает важ нейшее свойство линейных электрических цепей, на котором основаны многие ме тоды анализа линейных цепей.

Это свойство состоит в том, что реакция линейных электрических цепей на произвольное внешнее воздействие, представляющее собой линейную ком­ бинацию более простых воздействий, равна линейной комбинации реакций, вызванных каждым из простых воздействий в отдельности.

Из принципа наложения следует, что ток или напряжение любой ветви линейной электрической цепи, содержащей наряду с пассивными элементами зависимые и независимые источники тока и напряжения, равны сумме частич­ ных токов или напряжений, вызванных действием каждого из независимых ис­ точников в отдельности.

Пусть цепь содержит независимые источники только одного типа, например источники напряжения. Контурный ток произвольного контура этой цепи может быть определен из выражения (4.11). Представляя все входящие в это выражение контурные ЭДС в виде алгебраической суммы ЭДС входящих в контур источников напряжений , и приводя подобные члены, получаем

,

где N — число независимых источников ЭДС, входящих в состав цепи; Ykj — коэффи циенты, представляющие собой алгебраические суммы слагаемых вида ∆ik /∆.

Так как ∆ и ∆ik определяются только параметрами матрицы контурных сопро тивлений, т. е. параметрами пассивных элементов цепи и коэффициентами управле

ток гo контура, вызванный действием источника ЭДС .

Действительно, если все входящие в цепь независимые источники ЭДС, кроме , выключены (заменены короткозамыкающими перемычками), то ток k го контура

. 4.23

Следовательно, контурный ток любого контура линейной электрической цепи, содержащей независимые источники напряжения, равен сумме частичных токов, вызванных действием каждого независимого источника напряжения в отдельности:

352

токов (напряжений). Для определения частичных токов (напряжений) используют схемы замещения цепи, получаемые из исходной схемы путем выключения всех неза­ висимых источников, кроме одного, вызывающего соответствующий частичный ток

(напряжение). Таким образом, задача анализа сложной цепи, содержащей несколько независимых источников энергии, заменяется рядом более простых задач исследо вания цепей с одним независимым источником.

Следует обратить внимание на то, что при определении частичных токов вы ключаются только независимые источники тока или напряжения. Параметры зави симых источников учитываются в матрице узловых проводимостей или контурных сопротивлений и при нахождении частичных токов (напряжений) эти источники не выключаются.

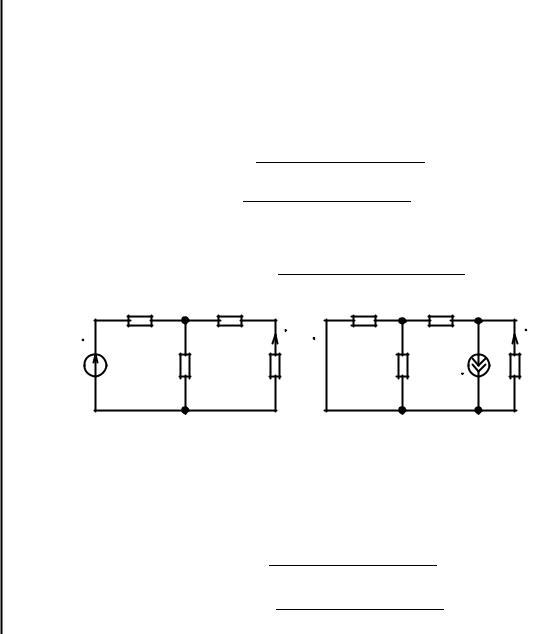
Пример4.10. Используя метод наложения, определим ток б электрической цепи, комплексная схема замещения которой приведена на рис. 4.2, а.

В соответствии с принципом наложения представим ток б в виде суммы двух час тичных токов б и б , вызванных действием источника напряжения и источника тока соответственно. Схемы замещения для расчета частичных токов приведены на рис. 4.10, а, б. Осуществляя эквивалентные преобразования участков цепей со смешанным соединением элементов, найдем частичные токи:

;

.

Суммируя эти токи, получим искомый ток:

.

Рис. 4.10. К примеру 4.10

Из полученных выражений следует, что комплексный коэффициент передачи цепи по току от зажимов 5 — 5' к зажимам 6 — 6' и комплексная передаточная проводимость этой цепи от зажимов 1 — 1’ к зажимам 6 — 6' номера зажимов совпадают с номерами вет вей имеют вид

;

.

Метод наложения оказывается весьма эффективным и при анализе линейных цепей, находящихся под воздействием колебаний сложной формы. В этом случае сложное внешнее воздействие представляют в виде конечной или бесконечной сум

354

мы колебаний более простой формы, реакция цепи, на воздействие которых может быть получена с помощью известных методов (подробнее см. книгу 6).

Необходимо отметить, что метод наложения применимтолькодляопределения токов или напряжений линейной электрической цепи и, даже в случае линейных це­ пей, не может быть использован для нахождения величин, которые не являются ли­ нейными функциями токов или напряжений. В частности, мощность, потребляемая каким либо участком линейной электрической цепи, находящейся под воздействи ем нескольких независимых источников, не равна сумме мощностей, потребляемых этим же участком при воздействии каждого независимого источника в отдельности.

Теорема взаимности

При изучении методов формирования уравнений электрического равновесия было установлено, что матрицы контурных сопротивлений и узловых проводимо стей линейных цепей, составленных только из сопротивлений, емкостей, индуктив ностей и независимых источников тока или напряжения, являются симметричными относительно главной диагонали. Можно показать, что симметричность этих мат риц не нарушится и в том случае, когда в цепи имеется произвольное число связан ных индуктивностей. На симметричности матриц узловых проводимостей и контур ных сопротивлений основано важное свойство линейных пассивных электрических цепей, которое формулируется в виде теоремы взаимности, или обратимости.

Рассмотрим линейную пассивную электрическую цепь, составленную из сопро тивлений, емкостей и индуктивностей (в том числе и связанных).

В соответствии с теоремой взаимности контурный ток k­го контура ли­ нейной пассивной цепи, вызванный действием единственного независимого источника напряжения, помещенного в i­й контур, равен контурному току i­гo контура, вызванному действием того же источника напряжения, перенесенно­ го из i­го контура в k­й, причем ориентация источника напряжения, помешен­ ного в какой­либо контур, относительно контурного тока этого контура в обоих случаях принимается одинаковой.

Рис. 4.11. К доказательству теоремы взаимности (внешнее воздействие задается в виде источника напряжения)

355

ветствии с выражением (4.11) контурный ток k го контура

. 4.25

Аналогичным образом находим контурный ток i го контура, вызванный дейст вием того же источника напряжения , перенесенного из 1 го контура в k й (рис. 4.11, б):

Выражения (4.25) и (4.26) отличаются только порядком следования индексов в алгебраических дополнениях ∆ , и ∆ . Учитывая симметричность матрицы контур ных сопротивлений анализируемой цепи относительно главной диагонали, нетруд но прийти к выводу, что ∆ = ∆ , а, следовательно, = .

Для случая, когда внешнее воздействие на цепь задается в виде независимого источника тока, теорема взаимности может быть сформулирована следующим обра зом.

Если независимый источник тока , подключенный к какой­либо паре за­ жимов линейной пассивной цени, вызывает на другой паре зажимов напряже­ ние (рис. 4.12, а), то этот же источник тока, подключенный ко второй царе зажимов (рис 4.12, б), вызовет на первой паре зажимов то же напряжение (ориентация источника тока относительно напряжения на зажимах, к которым он подключен, в обоих случаях принимается одинаковой).

Доказательство этой теоремы производится так же, как это было сделано при питании цепи от независимого источника напряжения.

Если электрическая цепь удовлетворяет теореме взаимности (в любой форму лировке), то говорят, что она обладает взаимностью (обратимостью). Электрические цепи, обладающие взаимностью, называются взаимными (обратимыми). Если электрическая цепь не обладает взаимностью, то она является невзаимной (необ­ ратимой). К необратимым цепям относятся, в частности, нелинейные цепи (элемен ты матриц контурных сопротивлений и узловых проводимостей таких цепей зави сят от токов или напряжений ветвей) и цепи, содержащие зависимые источники (матрицы контурных сопротивлений и узловых проводимостей таких цепей, как

Рис. 4.12. К доказательству теоремы взаимности (внешнее воздействие задается в виде источника тока)

356