
- •Аннотация
- •Оглавление
- •Дорогие читатели!
- •Предисловие
- •Введение
- •Книга 1. Основные понятия теории цепей
- •Модуль 1.1. Основные определения
- •Электрическая цепь
- •Электрический ток
- •Напряжение
- •Электродвижущая сила
- •Мощность и энергия
- •Схема электрической цепи
- •Вопросы для самопроверки
- •Модуль 1.2. Идеализированные пассивные элементы
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Дуальные элементы и цепи
- •Схемы замещения реальных элементов электрических цепей
- •Вопросы для самопроверки
- •Задачи
- •Модуль 1.3. Идеализированные активные элементы
- •Идеальный источник напряжения
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.4. Топология цепей
- •Схемы электрических цепей. Основные определения
- •Понятие о компонентных и топологических уравнениях. Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.5. Уравнения электрического равновесия цепей
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Классификация электрических цепей
- •Вопросы для самопроверки
- •Ответы
- •Модуль 2.1. Анализ линейных цепей с источниками гармонических токов и напряжений
- •Понятие о гармонических функциях
- •Линейные операции над гармоническими функциями
- •Среднее, средневыпрямленное и действующее значения гармонических токов и напряжений
- •Дифференциальное уравнение цепи при гармоническом воздействии
- •Вопросы для самопроверки
- •Модуль 2.2. Метод комплексных амплитуд
- •Понятие о символических методах
- •Комплексные числа и основные операции над ними
- •Операции над комплексными изображениями гармонических функций
- •Комплексные сопротивление и проводимость пассивного участка цепи
- •Порядок анализа цепи методом комплексных амплитуд
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.3. Идеализированные пассивные элементы при гармоническом воздействии
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Делители напряжения и тока
- •Вопросы для самопроверки
- •Задачи
- •Мгновенная мощность пассивного двухполюсник
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Коэффициент мощности
- •Согласование источника энергии с нагрузкой
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.6. Преобразования электрических цепей
- •Понятие об эквивалентных преобразованиях
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное преобразование
- •Комплексные схемы замещения источников энергии
- •Перенос источников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.7. Цепи с взаимной индуктивностью
- •Понятие о взаимной индуктивности
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Понятие о линейных трансформаторах
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 3. Частотные характеристики и резонансные явления
- •Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики цепей с одним реактивным элементом
- •Понятие о резонансе в электрических цепях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.2. Последовательный колебательный контур
- •Cхемы замещения и параметры элементов контура
- •Энергетические процессы в последовательном колебательном контуре
- •Входные характеристики
- •Передаточные характеристики
- •Избирательные свойства последовательного колебательного контура
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.3. Параллельный колебательный контур
- •Схемы замещения
- •Параллельный колебательный контур основного вида
- •Параллельный колебательный контур с разделенной индуктивностью
- •Параллельный колебательный контур с разделенной емкостью
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.4. Связанные колебательные контуры
- •Общие сведения
- •Схемы замещения
- •Настройка связанных контуров
- •Частотные характеристики
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Общие сведения
- •Методы, основанные на непосредственном применении законов Кирхгофа
- •Метод контурных токов
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.2. Основные теоремы теории цепей
- •Принцип наложения
- •Теорема взаимности
- •Теорема компенсации
- •Автономные и неавтономные двухполюсники
- •Теорема об эквивалентном источнике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.3. Метод сигнальных графов
- •Общие сведения
- •Преобразования сигнальных графов
- •Применение сигнальных графов к анализу цепей
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 5. Нелинейные резистивные цепи
- •Модуль 5.1. Постановка задачи анализа нелинейных резистивных цепей
- •Вводные замечания
- •Нелинейные резистивные элементы
- •Уравнения электрического равновесия нелинейных резистивных цепей
- •Вопросы для самопроверки
- •Модуль 5.2. Графические методы анализа нелинейных резистивных цепей
- •Простейшие преобразования нелинейных резистивных цепей
- •Определение рабочих точек нелинейных резистивных элементов
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Задача аппроксимации
- •Выбор аппроксимирующей функции
- •Определение коэффициентов аппроксимирующей функции
- •Вопросы для самопроверки
- •Задачи
- •Нелинейное сопротивление при гармоническом воздействии
- •Понятие о режимах малого и большого сигнала
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 6. Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами
- •Модуль 6.1. Задача анализа переходных процессов
- •Возникновение переходных процессов. Понятие о коммутации
- •Законы коммутации
- •Общий подход к анализу переходных процессов
- •Определение порядка сложности цепи
- •Вопросы для самопроверки
- •Модуль 6.2. Классический метод анализа переходных процессов
- •Свободные и вынужденные составляющие токов и напряжений
- •Порядок анализа переходных процессов классическим методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.3. Операторный метод анализа переходных процессов
- •Преобразование Лапласа и его применение к решению дифференциальных уравнений
- •Порядок анализа переходных процессов операторным методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.4. Операторные характеристики линейных цепей
- •Реакция цепи на экспоненциальное воздействие
- •Понятие об операторных характеристиках
- •Методы определения операторных характеристик
- •Дифференцирующие и интегрирующие цепи
- •Вопросы для самопроверки
- •Единичные функции и их свойства
- •Переходная и импульсная характеристики линейных цепей
- •Методы определения временных характеристик
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Определение реакции цепи на произвольное внешнее воздействие
- •Определение реакции цепи на произвольное внешнее воздействие по ее переходной характеристике
- •Определение реакции цепи на произвольное внешнее воздействие по ее импульсной характеристике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 7. Основы теории четырехполюсников и многополюсников
- •Модуль 7.1. Многополюсники и цепи с многополюсными элементами
- •Задача анализа цепей с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Классификация проходных четырехполюсников
- •Основные уравнения и первичные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров неавтономных проходных четырехполюсников
- •Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.4. Невзаимные проходные четырехполюсники
- •Идеальные усилители напряжения и тока
- •Однонаправленные цепи и цепи с обратной связью
- •Идеальные операционные усилители
- •Преобразователи сопротивления
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.5. Электрические фильтры
- •Классификация электрических фильтров
- •Реактивные фильтры
- •Активные фильтры
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 8. Цепи с распределенными параметрами
- •Модуль 8.1. Задача анализа цепей с распределенными параметрами
- •Общие сведения
- •Общее решение дифференциальных уравнений длинной линии
- •Вопросы для самопроверки
- •Волновые процессы в однородной длинной линии
- •Режим стоячих волн
- •Режим смешанных волн
- •Вопросы для самопроверки
- •Задачи
- •Проходной четырехполюсник с распределенными параметрами
- •Входное сопротивление отрезка однородной длинной линии
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Распределение напряжения и тока в однородной линии без потерь при произвольном внешнем воздействии
- •Вопросы для самопроверки
- •Задачи
- •Модуль 8.5. Цепи с распределенными параметрами специальных типов
- •Резистивные линии
- •Неоднородные линии
- •Вопросы для самопроверки
- •Задачи
- •Ответы
- •Книга 9. Синтез электрических цепей
- •Модуль 9.1. Задача синтеза линейных электрических цепей
- •Понятие физической реализуемости
- •Основные этапы синтеза цепей
- •Вопросы для самопроверки
- •Понятие о положительных вещественных функциях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.3. Методы реализации реактивных двухполюсников
- •Методы выделения простейших составляющих (метод Фостера)
- •Метод разложения в цепную дробь (метод Кауэра)
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.4. Основы синтеза линейных пассивных четырехполюсников
- •Задача синтеза четырехполюсников
- •Методы реализации пассивных четырехполюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 10. Методы автоматизированного анализа цепей
- •Модуль 10.1. Задача автоматизированного анализа цепей
- •Понятие о ручных и машинных методах анализа цепей
- •Общие представления о программах машинного анализа цепей
- •Вопросы для самопроверки
- •Топологические матрицы и топологические уравнения
- •Свойства топологических матриц
- •Компонентные матрицы и компонентные уравнения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Методы узловых напряжений и контурных токов
- •Метод переменных состояния
- •Формирование уравнений состояния в матричной форме
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 10.4. Особенности современных программ автоматизированного анализа цепей
- •Выбор методов формирования уравнений электрического равновесия. Понятие о поколениях программ автоматизированного анализа цепей
- •Вопросы для самопроверки
- •Ответы
- •Заключение
- •Приложения
- •Приложение 1. Таблица оригиналов и изображений по Лапласу
- •Приложение 2. Основные уравнения проходных четырёхполюсников
- •Приложение 3. Соотношения между первичными параметрами проходных четырехполюсников
- •Приложение 5. Соотношения между первичными параметрами взаимных и симметричных четырехполюсников
- •Приложение 6. Приставки для образования кратных и дольных единиц
- •Приложение 7. Инструкция для работы с Самоучителем по курсу «Основы теории цепей»
- •Список литературы
Модуль 2.6. Преобразования электрических цепей
Цель модуля: изучение методов преобразования пассивных и активных элек трических цепей.
Понятие об эквивалентных преобразованиях
Анализ процессов в электрических цепях во многих случаях может быть суще ственно упрощен за счет использования различных преобразований, в результате которых отдельные участки идеализированных цепей заменяются другими участ ками, более удобными для анализа.
Два участка идеализированной электрической цепи называются эквивалент ными, если при замене одного из этих участков другим токи и напряжения осталь ной части цепи не изменяются. Преобразования электрических цепей, в результате которых некоторые участки электрической цепи заменяются эквивалентными им участками, называются эквивалентными. Из определения эквивалентных участков следует, что они должны иметь одинаковое число внешних выводов, причем в про цессе эквивалентных преобразований токи этих выводов и напряжения между ними должны оставаться неизменными.
Эквивалентные участки электрических цепей обладают свойствами симмет ричности (если цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А), реф лексивности (цепь А является эквивалентной самой себе) и транзистивности(если цепь А эквивалентна цепи Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными). Если эквивалентность двух участков электрической цепи выпол няется при любых значениях внешних воздействий, то такие участки являются полностью эквивалентными. Различия между ними не могут быть установлены с помощью каких либо измерений, проводимых на внешних выводах. Если эквива лентность двух участков соблюдается только при определенном значении внешних воздействий, то такие участки являются частично эквивалентными (эквивалент ными при заданных условиях). Так, два участка линейной электрической цепи, на ходящейся под гармоническим воздействием, могут быть либо полностью эквива лентными, либо частично эквивалентными при заданной частоте внешнего воздей ствия.
Эквивалентные преобразования электрических цепей основаны на эквива лентных (равносильных) преобразованиях соответствующих систем уравнений электрического равновесия. Каждое равносильное преобразование системы уравне ний электрического равновесия исходной цепи (приведение подобных членов исключе ние неизвестных, замена переменных и т. д.) приводит к эквивалентному преобразо ванию моделирующей цепи. Соответственно изменяется и условное графическое изо бражение моделирующей цепи — схема цепи. На практике преобразования электри ческих цепей проводят, как правило, без составления систем уравнений электриче ского равновесия, путем непосредственного преобразования схем по определенным правилам. Систему уравнений электрического равновесия цепи записывают для уже преобразованной цепи, схема которой имеет достаточно простой вид.
163
Участки цепей с последовательным соединением элементов
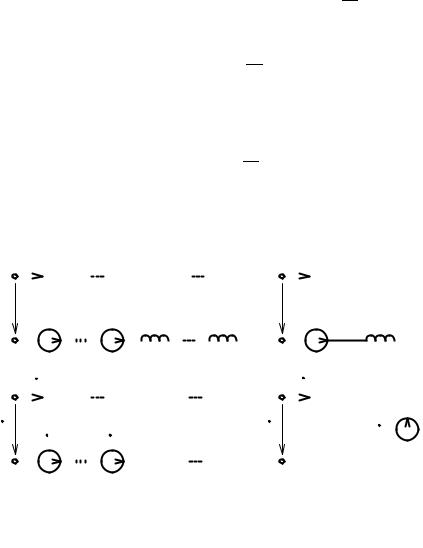
Рассмотрим неразветвленную электрическую цепь (рис. 2.32, а), содержащую N сопротивлений, М емкостей, К индуктивностей и неуправляемых источников на пряжения (обобщенная одноконтурная цепь). Так как через все элементы цепи про текает один и тот же ток i, то уравнение электрического равновесия, составленное на основе второго закона Кирхгофа и компонентных уравнений, может быть записа но в следующем виде:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
d |
|
1 |
|
|
d |
d |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
d |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
2.129 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|||||||||||
После приведения подобных членов (2.129) |
принимает вид |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
d |
|
|
|
d |
|
|
эк , |
|
|
|
|
|
|
|
2.130 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
эк |
|
|
|
|
эк |
|
|
эк |
d |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
где эк ∑ |
; |
|
|
|
|
|
∑ |
|
|
|
; |
|
|
эк ∑ |
|
|
|
|
|
|
; эк |
∑ |
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
эк |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.32. Преобразование участка цепи с последовательным соединением элементов
Уравнению (2.130) соответствует преобразованная цепь, схема которой изо бражена на рис. 2.32, б. Таким образом, ток и напряжение на зажимах обобщенной одноконтурной цепи не изменятся, если каждую из групп последовательно вклю ченных однотипных элементов заменить одним эквивалентным элементом, пара метр которого Rэк, Сэк, Lэк и eэк рассчитывается в соответствии с (2.130).
Из выражения (2.130) следует, что при последовательном включении сопротив лений, индуктивностей и источников напряжения параметры эквивалентного эле мента Rэк, Lэк и eэк равны сумме параметров последовательно включенных элементов соответствующего типа.
164
При этом суммирование ЭДС источников напряжения производится алгебраи чески с учетом их знаков, которые определяются тем, совпадает или не совпадает направление ЭДС с направлением обхода контура. Очевидно, что Rэк и Lэк не могут иметь меньшие значения, чем сопротивление и индуктивность любого из последо вательно включенных элементов. При последовательном соединении N одинаковых сопротивлений R или индуктивностей L параметр эквивалентного элемента Rэк или Lэк будет в N раз больше, чем параметр каждого из последовательно включенных элементов.
При последовательном включении емкостей значение величины, обратной Сэк, определяется как сумма величин, обратных каждой из последовательно включенных емкостей Сi. Очевидно, что эквивалентная емкость Сэк будет меньше любой из после довательно включенных емкостей. При последовательном включении M одинаковых емкостей эквивалентная емкость Сэк будет в M раз меньше каждой из последова тельно включенных емкостей.
Если обобщенная одноконтурная цепь находится под гармоническим воздей ствием, то от эквивалентной схемы для мгновенных значений (рис. 2.32, а) удобнее перейти к эквивалентной схеме для комплексных действующих значений (рис. 2.32, в). Уравнение электрического равновесия такой цепи, составленное на основании закона Ома и второго закона Кирхгофа в комплексной форме, имеет следующий вид:
.
После очевидных преобразований получаем
где эк ∑ |
∑ |
эк |
эк , |
2.131 |
∑ |
; эк ∑ |
. |
Комплексная схема замещения цепи, соответствующая уравнению (2.131), при ведена на рис. 2.32, г.
Таким образом, любой участок электрической цепи, представляющий со бой последовательное соединение произвольного числа идеализированных неуправляемых источников напряжения и пассивных двухполюсников, при гармоническом воздействии может быть заменен ветвью, содержащей один ис точник напряжения, ЭДС которого равна алгебраической сумме ЭДС всех по следовательно включенных источников, и один пассивный двухполюсник, комплексное сопротивление которого равно сумме комплексных сопротивле ний всех последовательно включенных пассивных двухполюсников.
Участки цепей с параллельным соединением элементов
Пусть электрическая цепь (рис. 2.33, а) состоит из параллельно соединенных N сопротивлений, М емкостей, К индуктивностей и ν неуправляемых источников тока (обобщенная двухузловая цепь). Все элементы цепи находятся под одним и тем же
165
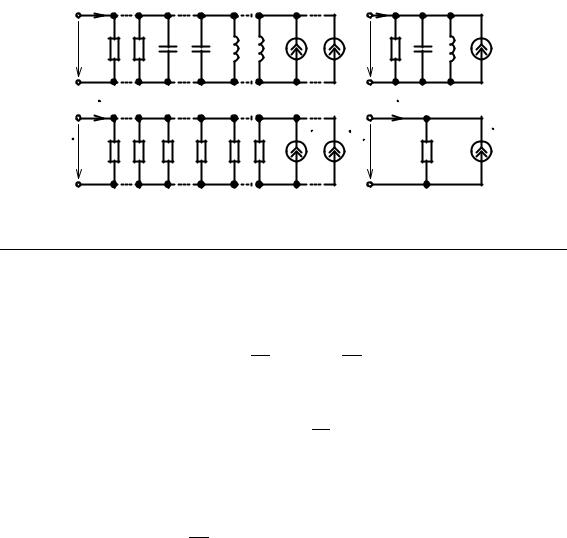
Рис. 2.33. Преобразование участка цепи с параллельным соединением элементов
напряжением и, поэтому уравнение электрического равновесия, составленное на ос новании первого закона Кирхгофа, может быть записано в виде
|
|
|
1 |
|
|
1 |
|
|
|
|
d |
|
|
|
d |
|
1 |
|
d |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
d |
|
1 |
|
d |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
. |
2.132 |
||
|
После приведения подобных членов получаем |
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
|
|
|
d |
1 |
|
|
d |
эк, |
|
|
|
|
2.133 |
|||||||||
|
|
|
|
|
|
|
эк |
|
эк |
d |
|
эк |
|
|
|
|
|
|
||||||||
где |
|
∑ |
|
; эк ∑ |
; |
|
|
|
∑ |
|
; |
|
эк |
∑ |
. |
|
||||||||||
эк |
|
эк |
|
|
|
|
||||||||||||||||||||
Уравнению (2.133) соответствует преобразованная цепь, схема которой приве дена на рис. 2.33, б. Очевидно, что ток и напряжение на зажимах обобщенной двухуз ловой цепи не изменятся, если каждую из групп параллельно включенных однотипных элементов заменить одним эквивалентным элементом, параметры которого Rэк, Сэк, Lэк и jэк рассчитываются в соответствии с (2.133).
Из выражения (2.133) следует, что при параллельном включении емкостей и источников тока параметры эквивалентного элемента Сэк, jэк равны сумме парамет ров параллельно включенных элементов соответствующего типа. При этом сумми рование токов источников тока производится алгебраически с учетом их знаков, оп ределяемых ориентацией источников относительно узла, для которого составляется уравнение (2.133). Очевидно, что значение Сэк превышает любую из параллельно включенных емкостей С1, …, СM. При параллельном соединении M одинаковых ем костей Сэк=M·C .
166
При параллельном включении сопротивлений или индуктивностей значения ве личин, обратных Rэк и Lэк , определяются как сумма значений всех величин, обратных параллельно включенным сопротивлениям Ri или индуктивностям Li.
Очевидно, что значения Rэк и Lэк будут меньше, чем сопротивление или индук тивность любого из параллельно включенных элементов соответствующего типа.
При параллельном включении |
N |
одинаковых сопротивлений |
R |
или индуктивно |
|||||||
стей |
L R |
эк = |
R/N |
, а |
L |
эк = |
L/N |
|
|
|
|
|
|
|
. |
|
|
|
|
||||
Для рассмотрения параметров обобщенной двухузловой цепи при гармониче ском воздействии воспользуемся комплексной схемой замещения этой цепи (рис. 2.33, в). Уравнение электрического равновесия цепи в комплексной форме может быть записано следующим образом:
или |
|
|
эк |
эк , |
2.134 |
|
где эк ∑ |
∑ |
∑ |
||||
; эк |
∑ |
. |
Комплексная схема замещения цепи, соответствующая уравнению (2.134), изо бражена на рис. 2.33, г.
Таким образом, любой участок электрической цепи, представляющий со бой параллельное соединение произвольного числа идеализированных пас сивных двухполюсников, может быть заменен одним пассивным двухполюсни ком, комплексная проводимость которого равна сумме комплексных проводи мостей всех параллельно включенных двухполюсников. Произвольное число параллельно включенных идеализированных источников тока может быть за менено одним источником, комплексное действующее значение тока которого равно алгебраической сумме комплексных действующих значений токов всех параллельно включенных источников.
Переходя в (2.134) от комплексных проводимостей к комплексным сопротив лениям, находим эквивалентное комплексное входное сопротивление Zэк группы параллельно включенных идеализированных пассивных двухполюсников:
1 |
1 |
1 |
1 |
. |
2.135 |
|||
эк |
|
|
|
|
|
|
||
Выражения, подобные (2.134) и (2.135), можно получить для комплексной про водимости и комплексного сопротивления любого участка цепи, являющегося па раллельным соединением произвольного числа идеализированных пассивных двух полюсников с заданным комплексным входным сопротивлением Zi или комплекс ной входной проводимостью Yi:
167
