
- •Аннотация
- •Оглавление
- •Дорогие читатели!
- •Предисловие
- •Введение
- •Книга 1. Основные понятия теории цепей
- •Модуль 1.1. Основные определения
- •Электрическая цепь
- •Электрический ток
- •Напряжение
- •Электродвижущая сила
- •Мощность и энергия
- •Схема электрической цепи
- •Вопросы для самопроверки
- •Модуль 1.2. Идеализированные пассивные элементы
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Дуальные элементы и цепи
- •Схемы замещения реальных элементов электрических цепей
- •Вопросы для самопроверки
- •Задачи
- •Модуль 1.3. Идеализированные активные элементы
- •Идеальный источник напряжения
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.4. Топология цепей
- •Схемы электрических цепей. Основные определения
- •Понятие о компонентных и топологических уравнениях. Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.5. Уравнения электрического равновесия цепей
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Классификация электрических цепей
- •Вопросы для самопроверки
- •Ответы
- •Модуль 2.1. Анализ линейных цепей с источниками гармонических токов и напряжений
- •Понятие о гармонических функциях
- •Линейные операции над гармоническими функциями
- •Среднее, средневыпрямленное и действующее значения гармонических токов и напряжений
- •Дифференциальное уравнение цепи при гармоническом воздействии
- •Вопросы для самопроверки
- •Модуль 2.2. Метод комплексных амплитуд
- •Понятие о символических методах
- •Комплексные числа и основные операции над ними
- •Операции над комплексными изображениями гармонических функций
- •Комплексные сопротивление и проводимость пассивного участка цепи
- •Порядок анализа цепи методом комплексных амплитуд
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.3. Идеализированные пассивные элементы при гармоническом воздействии
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Делители напряжения и тока
- •Вопросы для самопроверки
- •Задачи
- •Мгновенная мощность пассивного двухполюсник
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Коэффициент мощности
- •Согласование источника энергии с нагрузкой
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.6. Преобразования электрических цепей
- •Понятие об эквивалентных преобразованиях
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное преобразование
- •Комплексные схемы замещения источников энергии
- •Перенос источников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.7. Цепи с взаимной индуктивностью
- •Понятие о взаимной индуктивности
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Понятие о линейных трансформаторах
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 3. Частотные характеристики и резонансные явления
- •Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики цепей с одним реактивным элементом
- •Понятие о резонансе в электрических цепях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.2. Последовательный колебательный контур
- •Cхемы замещения и параметры элементов контура
- •Энергетические процессы в последовательном колебательном контуре
- •Входные характеристики
- •Передаточные характеристики
- •Избирательные свойства последовательного колебательного контура
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.3. Параллельный колебательный контур
- •Схемы замещения
- •Параллельный колебательный контур основного вида
- •Параллельный колебательный контур с разделенной индуктивностью
- •Параллельный колебательный контур с разделенной емкостью
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.4. Связанные колебательные контуры
- •Общие сведения
- •Схемы замещения
- •Настройка связанных контуров
- •Частотные характеристики
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Общие сведения
- •Методы, основанные на непосредственном применении законов Кирхгофа
- •Метод контурных токов
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.2. Основные теоремы теории цепей
- •Принцип наложения
- •Теорема взаимности
- •Теорема компенсации
- •Автономные и неавтономные двухполюсники
- •Теорема об эквивалентном источнике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.3. Метод сигнальных графов
- •Общие сведения
- •Преобразования сигнальных графов
- •Применение сигнальных графов к анализу цепей
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 5. Нелинейные резистивные цепи
- •Модуль 5.1. Постановка задачи анализа нелинейных резистивных цепей
- •Вводные замечания
- •Нелинейные резистивные элементы
- •Уравнения электрического равновесия нелинейных резистивных цепей
- •Вопросы для самопроверки
- •Модуль 5.2. Графические методы анализа нелинейных резистивных цепей
- •Простейшие преобразования нелинейных резистивных цепей
- •Определение рабочих точек нелинейных резистивных элементов
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Задача аппроксимации
- •Выбор аппроксимирующей функции
- •Определение коэффициентов аппроксимирующей функции
- •Вопросы для самопроверки
- •Задачи
- •Нелинейное сопротивление при гармоническом воздействии
- •Понятие о режимах малого и большого сигнала
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 6. Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами
- •Модуль 6.1. Задача анализа переходных процессов
- •Возникновение переходных процессов. Понятие о коммутации
- •Законы коммутации
- •Общий подход к анализу переходных процессов
- •Определение порядка сложности цепи
- •Вопросы для самопроверки
- •Модуль 6.2. Классический метод анализа переходных процессов
- •Свободные и вынужденные составляющие токов и напряжений
- •Порядок анализа переходных процессов классическим методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.3. Операторный метод анализа переходных процессов
- •Преобразование Лапласа и его применение к решению дифференциальных уравнений
- •Порядок анализа переходных процессов операторным методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.4. Операторные характеристики линейных цепей
- •Реакция цепи на экспоненциальное воздействие
- •Понятие об операторных характеристиках
- •Методы определения операторных характеристик
- •Дифференцирующие и интегрирующие цепи
- •Вопросы для самопроверки
- •Единичные функции и их свойства
- •Переходная и импульсная характеристики линейных цепей
- •Методы определения временных характеристик
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Определение реакции цепи на произвольное внешнее воздействие
- •Определение реакции цепи на произвольное внешнее воздействие по ее переходной характеристике
- •Определение реакции цепи на произвольное внешнее воздействие по ее импульсной характеристике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 7. Основы теории четырехполюсников и многополюсников
- •Модуль 7.1. Многополюсники и цепи с многополюсными элементами
- •Задача анализа цепей с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Классификация проходных четырехполюсников
- •Основные уравнения и первичные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров неавтономных проходных четырехполюсников
- •Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.4. Невзаимные проходные четырехполюсники
- •Идеальные усилители напряжения и тока
- •Однонаправленные цепи и цепи с обратной связью
- •Идеальные операционные усилители
- •Преобразователи сопротивления
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.5. Электрические фильтры
- •Классификация электрических фильтров
- •Реактивные фильтры
- •Активные фильтры
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 8. Цепи с распределенными параметрами
- •Модуль 8.1. Задача анализа цепей с распределенными параметрами
- •Общие сведения
- •Общее решение дифференциальных уравнений длинной линии
- •Вопросы для самопроверки
- •Волновые процессы в однородной длинной линии
- •Режим стоячих волн
- •Режим смешанных волн
- •Вопросы для самопроверки
- •Задачи
- •Проходной четырехполюсник с распределенными параметрами
- •Входное сопротивление отрезка однородной длинной линии
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Распределение напряжения и тока в однородной линии без потерь при произвольном внешнем воздействии
- •Вопросы для самопроверки
- •Задачи
- •Модуль 8.5. Цепи с распределенными параметрами специальных типов
- •Резистивные линии
- •Неоднородные линии
- •Вопросы для самопроверки
- •Задачи
- •Ответы
- •Книга 9. Синтез электрических цепей
- •Модуль 9.1. Задача синтеза линейных электрических цепей
- •Понятие физической реализуемости
- •Основные этапы синтеза цепей
- •Вопросы для самопроверки
- •Понятие о положительных вещественных функциях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.3. Методы реализации реактивных двухполюсников
- •Методы выделения простейших составляющих (метод Фостера)
- •Метод разложения в цепную дробь (метод Кауэра)
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.4. Основы синтеза линейных пассивных четырехполюсников
- •Задача синтеза четырехполюсников
- •Методы реализации пассивных четырехполюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 10. Методы автоматизированного анализа цепей
- •Модуль 10.1. Задача автоматизированного анализа цепей
- •Понятие о ручных и машинных методах анализа цепей
- •Общие представления о программах машинного анализа цепей
- •Вопросы для самопроверки
- •Топологические матрицы и топологические уравнения
- •Свойства топологических матриц
- •Компонентные матрицы и компонентные уравнения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Методы узловых напряжений и контурных токов
- •Метод переменных состояния
- •Формирование уравнений состояния в матричной форме
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 10.4. Особенности современных программ автоматизированного анализа цепей
- •Выбор методов формирования уравнений электрического равновесия. Понятие о поколениях программ автоматизированного анализа цепей
- •Вопросы для самопроверки
- •Ответы
- •Заключение
- •Приложения
- •Приложение 1. Таблица оригиналов и изображений по Лапласу
- •Приложение 2. Основные уравнения проходных четырёхполюсников
- •Приложение 3. Соотношения между первичными параметрами проходных четырехполюсников
- •Приложение 5. Соотношения между первичными параметрами взаимных и симметричных четырехполюсников
- •Приложение 6. Приставки для образования кратных и дольных единиц
- •Приложение 7. Инструкция для работы с Самоучителем по курсу «Основы теории цепей»
- •Список литературы
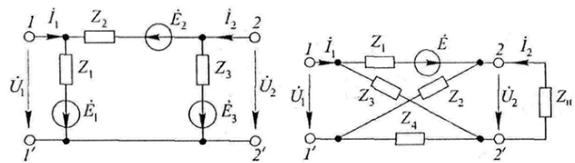
7.42. |
Определите напряжение |
на выходе автономного четырехполюсника |
|||||
рис. Т7.36 |
для |
2 ⁄ B; |
1 |
Ом; |
2 Ом; |
4 Ом; |
З Ом; н З Ом; |
4⁄ В.
7.43. По данным задачи 7.42 найдите отношение ⁄ на входе автономного четырехполюсника и сравните результат с входным сопротивлением пассивного че тырехполюсника, соответствующего заданному автономному.
Рис. Т7.35 |
Рис. Т7.36 |
7.44р. Коэффициенты основных уравнений автономного четырехполюсника заданы в форме . Найдите коэффициенты основных уравнений этого же четырех полюсника в форме .
7.45. Коэффициенты основных уравнений автономного четырехполюсника за
даны в форме . Определите. |
коэффициенты основных уравнений этого же четырех |
||
полюсника в форме |
|
и |
Т образной схемы замещения автономного |
7.46. Покажите, что ЭДС |
|||
четырехполюсника связаны с коэффициентами основных уравнений этого же четы рехполюсника в форме соотношениями ;
.
7.47. Покажите,чтотоки к и к П образнойсхемызамещенияавтономного че тырехполюсника связаны с коэффициентами основных уравнений этого же четы
рехполюсника в форме |
соотношениями |
|
к |
к |
; |
к |
к |
|
. |
|
и ток |
|
на входе автономного четырехполюс |
||||
7.48р. Выразите напряжение |
|
|||||||
ника через напряжение |
и ток . на его выходе и коэффициенты основных уравне |
|||||||
ний четырехполюсника в форме |
и |
|
ток |
на |
входе |
автономного че |
||
7.49. Выразите |
напряжение |
|
||||||
тырехполюсника через напряжение |
и ток |
. |
на его выходе и коэффициенты основ |
|||||
ных уравнений четырехполюсника в форме |
|
|
|
|
|
|
||
Решения и методические указания
7.10р. Преобразуя уравнения электрического равновесия цепи, составленные на основании законов Кирхгофа,
638
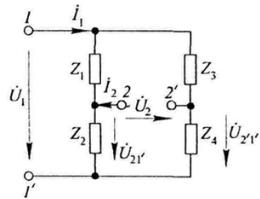
,
к виду, соответствующему основным уравнениям четырехполюсника в форме
,
⁄ ,
и сравнивая эти уравнения с основными уравнениями четырехполюсника в форме :
1. |
; |
, получаем |
1; |
0; |
; |
7.11р. Из основных уравнений четырехполюсника в форме |
(см. задачу 7. 10р) |
||||
найдите выражения для определения параметров по данным опытов холостого хода и короткого замыкания:
|
|
|
|
1; |
|
|
0; |
|
|
|
|
|
|
|
|||||
|
|
|
|
1⁄ ; |
|
|
1. |
и срав |
|
|
|
|
|
|
|||||
7.15м. Составьте компонентные уравнения связанных индуктивностей. |
|||||||||
ните их с основными уравнениями четырехполюсника в форме |
|
||||||||
|
7.16р. |
|
|
|
|
|
|
|
|
|
Придайте схеме рассматриваемого четырехполюсника более наглядный |
||||||||
вид (рис. Т7.37) и запишите основные. |
уравнения четырехполюсника в форме |
: |
|
||||||
; |
В режиме холостого хода на выходе ( |
0) |
|
|
|||||
|
|
|
|
; |
|
. |
|
пред |
|
|
|
|
|
|
|
||||
|
Как следует из полученных выражений и схемы рис. Т7.37, параметр |
||||||||
|
|
|
|
|
|
|
|
|
|
Рис. Т7.37
639
ставляет собой входное сопротивление четырехполюсника со стороны зажимов |
1 |
1' |
||||||
при холостом ходе на зажимах |
2 |
2' |
и численно равен входному сопротивлению |
|||||
двухполюсника, образованного. |
параллельным соединением двух ветвей с сопротив |
|||||||
лениями |
и |
Следовательно, |
|
|
||||
.
На основании второго закона Кирхгофа и закона Ома можно записать (рис.
Т7.37):
|
|
; |
; |
|
|
|
. |
|
|
|
|
⁄ |
при |
|
|
|
|||
Определив отсюда отношение напряжений |
|
0 и используя полу |
|||||||
ченное ранее выражение для |
найдем |
|
и |
⁄ |
. |
||||
Аналогичным образом определим параметры |
по результатам опыта |
||||||||
холостого хода на входе четырехполюсника ( |
0): |
|
|
|
; |
. |
|||
|
|
|
|||||||
Последнее равенство справедливо для любого линейного пассивного четырехпо люсника.
7.18м. Составьте матрицы параметров для каждого четырехполюсника. (Для мостового четырехполюсника используйте результаты решения задачи 7.16р.) Вы ясните, при каких условиях эти матрицы равны между собой.
7.20м. Используйте формулы перехода от к параметрам.
7.21р. Составьте уравнения электрического равновесия цепи, используя метод узловых напряжений:
Учитывая, что |
, и сравнивая, |
1⁄ |
; |
. |
|
|
полученные уравнения с основными урав |
||||||
нениями четырехполюсника в форме |
найдите |
|
1⁄ |
. |
||
; |
; |
|
; |
|
||
7.22р. Заменив источник тока |
|
с внутренним сопротивлением |
источ |
|||
ником напряжения |
с тем же внутренним сопротивлением и составив |
|||||
уравнения электрического равновесия цепи по методу контурных токов, определим выражения для параметров четырехполюсника:
; |
; |
; |
. |
640

Т образная схема замещения рассматриваемогочетырехполюсника приведена на рис. Т7.38. Параметры элементов эквивалентной схемы:
;
;
;
.
Рис. Т7.38
Как видно из сравнения рис. Т7.21 и Т7.38, каноническая эквивалентная схема рис. Т7.38 значительно проще, чем исходная схема (см. рис. Т7.21).
7.23р. Расчетные соотношения для определения параметров выводятся из основных уравнений четырехполюсника в форме :
;.
Параметры |
и |
, образующие певый столбец матрицы |
параметров, изме |
||||||||
ряются в режиме холостого хода на выходе (ключ |
разомкнут, |
|
0): |
||||||||
откуда |
|
|
; |
|
, |
|
|
||||
|
|
|
|
; |
|
|
. |
|
|
||
|
Следовательно, |
, параметр |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
и |
|
непосредственно выражается через напряжения |
|||||||||
измеренные в режиме холостого хода. Для определения |
выразим ток |
||||||||||
через известные напряжения |
и : |
⁄ н . |
|
|
|||||||
Таким образом,
1
.
н
641
Два других параметра определим по результатам измерения напряжений нагруженного четырехполюсника (ключ замкнут, 0). Из первого уравнения исходной системы получаем выражение для определения
а из второго уравнения находим |
н |
|
|
, |
|||||
⁄ |
|||||||||
н |
. |
||||||||
Определяя ток таким же образом, как и в режиме холостого хода, получим |
|||||||||
н |
1 |
|
|
|
|
|
|
. |
|
н |
|
|
|
|
|
|
|||
7.24м. Учтите, что направление тока |
|
в основных уравнениях четырехполюс |
|||||||
ника в форме противоположно направлению тока (см. рис. Т7.22).
7.27р. а) При последовательном соединении четырехполюсников матрица параметров составного четырехполюсника равна сумме матриц параметров со ставляющих его элементарных четырехполюсников:
28; |
7 |
Ом. |
7; |
10 |
|
б) При параллельном соединении четырехполюсников матрица параметров |
||
составного четырехполюсника равна сумме матриц параметров составляющих его
элементарных четырехполюсников. Используя формулы перехода |
|
|
⁄∆ ; |
|||||||||
|
⁄∆ |
; |
⁄∆ |
; |
⁄∆ , ∆ |
|
|
|
, определим |
|
||
параметры элементарных четырехполюсников: |
0,128; |
|
0,106 |
|
|
|
||||||
|
|
|
0,0667; |
0,0333 |
См; |
|
См. |
|
|
|||
Суммируя |
и |
, |
0,0333; |
0,267 |
0,106; |
0,255 |
|
|
||||
|
определим |
параметры составного четырехполюсника: |
|
|
||||||||
|
|
|
|
|
0,195; |
0,139 |
См. |
|
|
|
|
|
|
|
|
|
|
0,139; |
0,522 |
параметровсо |
|||||
в)Прикаскадномсоединениичетырехполюсниковматрица |
||||||||||||
ставного четырехполюсника равна произведению матриц |
параметров со |
перехо |
||||||||||
ставляющих его элементарных четырехполюсников. Используя |
формулы |
|||||||||||
да |
⁄ |
; |
( |
|
⁄ |
; |
|
1⁄ |
; |
|
⁄ |
, |
определим матрицы параметров элементарных четырехполюсников:
8; |
30 |
; |
2,4; |
9,4 |
0,5; |
2 |
0,2; |
1,2 . |
642
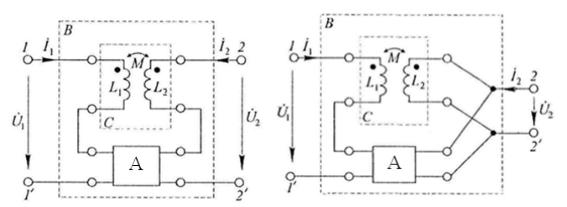
Перемножив И , найдем параметры составного четырехполюсника:
25,2; 111,2 . 1,6; 7,1
В матрицах параметров элементы главной диагонали безразмерны, а недиа гональные элементы имеют размерности Ом и См.
7.34м. Соединение четырехполюсников и является нерегулярным, поэтому суммировать матрицы первичных параметров элементарных четырехполюсников для определения первичных параметров составного четырехполюсника в данном случае недопустимо. Эти параметры следует находить непосредственно по схеме со ставного четырехполюсника.
7.35м. См. указание к задаче 7.34м. |
в виде последовательного соединения |
7.36р. Представим четырехполюсник |
|
двух элементарных четырехполюсников |
и (рис. Т7.39). Соединение четырехпо |
люсников является регулярным, поэтому применим правило суммирования матриц
параметров элементарных четырехполюсников: |
|
. параметры четы |
|||
рехполюсника |
. были найдены в задаче 7.15м: |
; |
|||
; |
|
|
Суммируя матрицы. |
A и |
, получим |
; |
7.37м. |
|
; |
|
|
|
|
Исследуемый четырехполюсник следует представить в виде последова |
|||
тельно параллельного соединения четырехполюсников и |
(рис. Т7.40). Соедине |
||||
ние четырехполюсников является регулярным, поэтому применимо правило сумми рования матриц параметров элементарных четырехполюсников: . Далее следует найти параметры элементарных четырехполюсников по их извест ным параметрам, записать матрицу и определить по ней с помощью формул перехода искомые параметры.
Рис. Т7.39 |
Рис. Т7.40 |
643

Рис. Т7.41
7.38м. Для ответа на вопрос задачи нужно найти напряжения холостого хода на зажимах 1 1' и 2 2' каждого четырехполюсника.
7.39р. параметры пассивного четырехполюсника, который получают из за данного автономного путем исключения всех независимых источников, были полу чены раньше (см. задачу 7.16р). Следовательно, остается найти напряжения холосто гохода х и х на входныхи выходных зажимахавтономной цепи.
Придадим схеме рис. Т7.33 более наглядный вид (рис. Т7.41, а). Как видно из рисунка, напряжения холостого хода между выводами четырехполюсника
х х
х х
где
х
;
,
. Следовательно,
;
|
Т образная |
х |
|
|
|
. |
||
|
|
|
|
|||||
|
бсхема замещения рассматриваемого четырехполюсника приведена |
|||||||
на рис. Т7.41, |
, где |
2 |
; |
|||||
; |
х |
х |
|
; |
2 |
; |
||
7.44р. |
|
; х |
х . |
|
|
|||
|
|
Уравнения автономного четырехполюсника в форме имеют вид |
||||||
|
|
|
|
|
|
х; |
|
х. |
|
Этим уравнениям соответствует Т образная схема замещения. Найдем из |
|||||||
этих уравнений токи |
и : |
|
|
|||||
∆ ∆ ∆
∆ ∆ ∆
х
х
∆х;
∆х,
644

где ∆ |
. |
|
Сравним полученный результат с основными уравнениями автономного четы |
||
рехполюсника в форме : |
к; |
к. |
Таким образом, найдена связь между токами к и |
к П образной схемы заме |
|
щения автономного четырехполюсника и коэффициентами основных уравнений че тырехполюсника в форме :
к
к
∆
∆
х
х
∆х;
∆х.
Формулы перехода |
от |
|
|
параметров |
|
автономного четырехполюсника |
к |
Y |
||||||||||
параметрам имеют такой же вид, как и для неавтономного четырехполюсника: |
|
|||||||||||||||||
7.48р. |
|
⁄∆ |
; |
|
|
⁄∆ |
; |
|
|
|
⁄∆ ; |
|
⁄∆ . |
имеет |
||||
вид: |
Система уравнений автономного четырехполюсника. |
в форме |
||||||||||||||||
|
|
|
|
х; |
|
|
|
|
|
|
х |
|
|
|
|
|||
Из второго уравнения системы получим |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
х. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставив это выражение в первое уравнение системы, найдем |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
х. |
|
|
|
Полученные уравнения для |
|
|
|
|
|
|
|
|
|
|||||||||
и можно рассматривать как уравнения авто |
||||||||||||||||||
номного |
четырехполюсника в |
форме |
: |
; |
|
|
х |
⁄ |
х; |
|||||||||
1⁄ |
; |
⁄ |
|
х,.где |
; |
|
|
|
⁄ |
|
|
|
; |
|||||
645
Модуль 7.3. Характеристические параметры и комплексные частотные ха рактеристики неавтономных проходных четырехполюсников
Цель модуля: введение понятия характеристических параметров, ознакомле ние с методами определения и применением характеристических параметров.
Комплексные частотные характеристики четырехполюсников при про извольной внешней нагрузке
Несмотря на то, что первичные параметры четырехполюсника представляют собой только некоторые комплексные частотные характеристики, измеренные в одном из предельных режимов (холостого хода или короткого замыкания), зная первичные параметры четырехполюсника, образующие любую из систем первичных параметров, можно найти его любые комплексные частотные характеристики при произвольной внешней нагрузке. Для примера покажем, как по известным значени
ям |
А |
параметров неавтономного проходного четырехполюсника можно определить |
||||||||
его комплексное входное сопротивление со стороны зажимов |
1—1' |
и ком |
||||||||
плексные коэффициенты передачи по напряжению |
и току |
от зажи |
||||||||
мов |
1—1' |
к зажимам |
2—2' |
при произвольной нагрузке |
Z |
|
|
|||
|
|
|
|
н2, подключенной к зажимам |
||||||
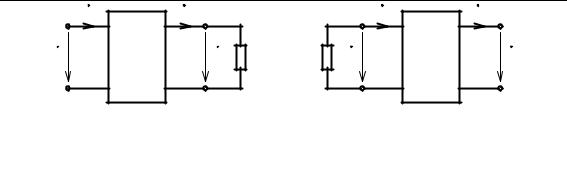
2—2' |
(рис. 7.33, а). |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
Ток и напряжение на выходных зажимах четырехполюсника в рассматривае мом режиме связаны соотношением / н , используя которое основные урав нения четырехполюсника в форме А (7.32) могут быть преобразованы к виду
⁄ |
н |
н |
⁄ |
н |
|
н |
; |
7.63 |
⁄ |
н |
н |
⁄ |
н |
|
н |
. |
|
Из уравнений (7.63) следует, что |
н |
|
|
н |
; |
|
7.64 |
|
|
⁄ |
|
н |
|
||||
|
⁄ |
н ⁄ |
н |
|
; |
|
7.65 |
|
|
⁄ |
1⁄ |
|
|
. |
|
7.66 |
|
В режиме холостого хода на зажимах 2 2 |
( н |
∞) коэффициент передачи че |
||||||
тырехполюсника по току равен нулю, а входное сопротивление со стороны зажимов
Рис. 7.33. К определению комплексных частотных характеристик проходного четы рехполюсника при произвольной нагрузке
646
1—1' и коэффициент передачи по напряжению от зажимов 1—1' к зажимам 2—2' оп ределяются выражениями
х |
⁄ ; |
х |
1⁄ . |
7.67 |
В режиме короткого замыкания на зажимах 2 2 ( н |
0) коэффициент пере |
|||
дачи по напряжению равен нулю, а входное сопротивление и коэффициент передачи по току характеризуются соотношениями
к |
|
|
⁄ ; |
к |
1⁄ . |
7.68 |
Рассмотрим случай так называемого |
обратного включения |
, когда сопротив |
||||
ление нагрузки |
1—1' |
|
н |
⁄ |
|
7.69 |
подключено к зажимам |
|
(рис. 7.33, б). Разрешая основные уравнения четырех |
||||
полюсника (7.32) относительно |
и и учитывая (7.69), получаем |
|
||||
н
н
⁄∆
⁄∆
н |
⁄ |
н ∆ |
; |
7.70 |
н |
⁄ |
н ∆ . |
|
Используя (7.70), определяем входное сопротивление четырехполюсника и ко эффициенты передачи четырехполюсника по напряжению и току в обратном вклю чении:
⁄ |
н |
⁄ |
н |
; |
7.71 |
⁄ |
н ∆ ⁄ |
н |
|
; |
7.72 |
|
∆ ⁄ |
н |
|
. |
7.73 |
В отличие от , и величины , и на зываются входным сопротивлением и коэффициентами передачи четырехполюсни ка по напряжению и току в прямом включении. В режиме холостого хода на зажимах
1—1' ( н ∞):
х |
⁄ ; |
врежиме короткого замыкания
к⁄ ;
х
к
∆ ⁄ , |
7.74 |
∆ ⁄ . |
7.75 |
По аналогичной методике выражения для любых комплексных частотных ха рактеристик четырехполюсника как в прямом, так и в обратном включении могут быть найдены также в терминах Y , Z , Н , G или B параметров.
Пусть к входным зажимам четырехполюсника подключен линеаризованный источник с внутренним сопротивлением н , а к выходным зажимам — сопро
647
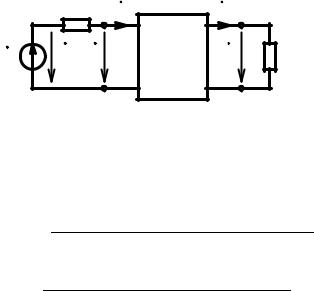
тивление нагрузки н (рис. 7.34). Отношение напряжения на выходе двусторонне нагруженного четырехполюсника к ЭДС линеаризованного источника
р⁄ ⁄
называется рабочим коэффициентом передачи четырехполюсника по напряже нию.
Рис. 7.34. К определению рабочего коэффициента передачи четырехполюсника по напряже нию
Учитывая, что |
н и |
н , получаем |
н
р
н
н .
нн н
Найденные выражения для комплексного входного сопротивления и ком плексного коэффициента передачи, учитывающие наличие нагрузки и внутреннего сопротивления источника, относятся к внешним (рабочим) параметрам четырехпо люсника.
Характеристические сопротивления неавтономного проходного четы рехполюсника
|
Характеристическими сопротивлениями четырехполюсника называют пару |
||||||||||
сопротивлений |
с и |
с , которые выбраны таким образом, что при подключении к |
|||||||||
зажимам |
2—2' |
сопротивления н |
с входное сопротивление четырехполюсника |
||||||||
со стороны зажимов |
1—1' |
равно |
с , а при подключении к зажимам |
1—1' |
сопротив |
||||||
ления н |
с |
входное сопротивление четырехполюсника со стороны зажимов |
2— |
||||||||
2' |
равно |
с . Сопротивление с |
называется |
характеристическим входным |
, a с |
||||||
― |
|
|
|
||||||||
характеристическим выходным сопротивлением четырехполюсника |
|
|
|
||||||||
|
|
|
|
|
|
|
. Подставляя в |
||||
выражения для входных сопротивлений четырехполюсника в прямом (7.64) и об
ратном (7.71) включениях н |
с , |
с ; н |
с , |
с и решая |
полученную систему уравнений: |
|
|
|
|
с с
с с
относительно с и с , находим
⁄
⁄
с;
с
648

с
с
⁄ |
; |
7.76 |
⁄ |
. |
7.77 |
Используя выражения (7.67), (7.68), (7.74) и (7.75), убеждаемся, что характери стическое входное сопротивление четырехполюсника может быть найдено как среднее геометрическое из его входных сопротивлений в прямом включении в ре жимах холостого хода и короткого замыкания:
с |
х |
к |
, |
а характеристическое выходное сопротивление как среднее геометрическое из его входных сопротивлений в обратном включении в режимах холостого хода и корот кого замыкания:
с |
х |
к |
, |
Таким образом, характеристические сопротивления четырехполюсника могут быть найдены непосредственно по результатам опытов холостого хода и короткого замыкания.
Четырехполюсник, к зажимам 2—2' которого подключено сопротивление
нс , будем называть четырехполюсником с согласованной нагрузкой на
выходе. В соответствии с (7.65), (7.66) коэффициенты передачи такого четырехпо люсника по току и напряжению от зажимов 1—1' к зажимам 2—2' определяются вы ражениями
|
|
|
|
н |
с |
|
|
|
|
|
|
|
|
1 |
|
|
; |
|
7.78 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
н |
с |
|
|
|
|
|
|
|
1 |
|
|
|
, |
|
7.79 |
||
откуда |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
с |
|
с |
|
|
|
|
||||||
Для четырехполюсника с |
|
|
|
|
|
|
|
|
|
|
|
|
( н |
с ) |
|||||||
согласованной нагрузкой на входе |
|||||||||||||||||||||
|
|
⁄ |
|
|
|
|
|
|
|
|
|
⁄ . |
|||||||||
аналогичным образом находим |
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
; |
|
7.80 |
|||||
|
|
|
|
н |
с |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆
. 7.81
нс
649
