4.1.3. Преобразование плотности вероятности

Пусть известна плотность вероятности случайной величины , действующей на нелинейный безынерционный элемент. Нужно найти плотность вероятности выходной случайной величины . Связь между и даётся нелинейной детерменированной зависимостью 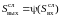. Если определяет однозначное соответствие между и в каждый рассматриваемый момент времени независимо от значений в предыдущие моменты времени, то и вероятности событий на входе и выходе НБЭ равны, т.е. . Учитывая, что плотности распределения вероятностей неотрицательные функции, получим

Если обратная функция неоднозначна, то

где , ...– значения входной величины, соответствующие рассматриваемому значению .

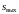Математическое ожидание и дисперсию случайной величины на выходе НБЭ можно записать соответственно как

Пример 4.1. Рассмотрим воздействие нормально распределённого случайного процесса с плотностью вероятности с НБЭ с симметричной квадратичной вольт-амперной характеристикой 1 (рис. 4.2), которую можно реализовать, например, с помощью двухтактного включения двух диодов, обладающих вблизи нуля квадратичными зависимостями.

При заданной полярности напряжения (см. рис. 4.3) через диод проходит ток , а при обратной через диод – ток . Полагая 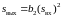, и учитывая, что какому-либо фиксированному значению соответствуют два знаения , а именно и 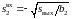, по формуле (4.9) найдём

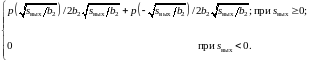
Подставляя в выражение для плотности вероятности

получим окончательно

Плотность вероятности тока в цепи с квадратичной вольт-амперной характеристикой показана на рис. 4.4 (при ).

4.1.4. Корреляционная функция и спектральная плотность на выходе нбэ

Прямое определение спектральной плотности случайного процесса на выходе НБЭ по известному спектру на входе не представляется возможным. Поэтому вначале необходимо определить корреляционную функцию, а затем, применив к ней преобразование Фурье, найти спектральную плотность.

Если на входе НБЭ с характеристикой 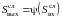действует центрированный стационарный случайный процесс , то корреляционная функция на выходе может быть определена так:

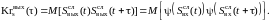
Для усреднения произведения должна быть известна двумерная плотность вероятности входного процесса 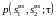. Если эта плотность вероятности известна, то корреляционная функция может быть представлена в виде следующего выражения:

Вычисление этого интеграла удаётся осуществить далеко не во всех практически важных случаях.

Рассмотрим важный для практики случай, когда НБЭ описывается функцией . Если процесс на входе НБЭ нормальный, то функцию можно вычислить по известной корреляционной функции процесса на входе. Обозначим среднеквадратическое значение реализации случайного процесса через , тогда , а нормированная функция корреляции

.

Двумерная плотность вероятности определяется зависимостью

Подставляя (4.12) в (4.11) и учитывая, что , получим

Вычисление интеграла в (4.13), приведённое в [22], даёт следующий результат

Определим спектральную плотность случайного процесса на выходе НБЭ

Первое слагаемое представляет собой произведение -функции на , т.е. . Второй интеграл в (4.15) представляет собой преобразование Фурье от произведения двух функций , которое равно свёртке их фурье-образов. С учётом изложенного, зависимость (4.15) принимает вид

Дисперсия выходного случайного процесса определяется зависимостью