1.7.2. Свойства выборочной функции

Функция (1.61)

(1.65)

называемая выборочной функцией представляет собой двумерную -решётку (рис. П.3) из функций с амплитудой . Рассмотрим её основные свойства.

1. Функция s_выб имеет размерность исходного сигнала s.

2. Объем выборки пропорционален сумме выборочных значе­ний

.

3. Спектр выборочной функции равен бесконечной двумерной сумме дискретно смещенных финитных спектров исходного сигнала и совпадает со вспомогательной функцией (1.62) на рис. 1.7б, так что

(1.66)

4. Свёртка 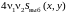с интерполяционной функцией 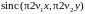восстанавливает исходный сигнал с помощью ряда Котельникова 1.64), который можно записать в виде .

На практике часто используют выборочную функцию , отличающуюся от (1.64) постоянным коэффициентом. Ее свойства совпадают со свойствами функции .

1.7.3. Переналожение спектров

Пусть выборка осуществляется через произвольные промежутки , т.е. . В этом случае вспомогательная функция (1.62) имеет вид

. (1.62 )

Подставляя ее в (1.63), в результате обратного преобразования Фурье получим выражение для обобщенного ряда Котельникова

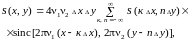(1.64 )

которое при переходит в ряд Котельникова (1.64).

Если теперь интервалы выборки т.е. , то для выборочной функции (1.65) имеем

. (1.67)

В свою очередь для спектра выборочной функции по аналогии с (1.66)

. (1.62 )

На рис. 1.9 а,б приведены одномерные ПЧС и . Так как

, (1.68)

то использование низкочастотного ПЧФ с передаточной функцией 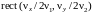при передаче по каналу связи в виде (1.67) не позволяет выделить ПЧС исходного сигнала в чистом виде. В отфильтрованном ПЧС (1.68) будут присутствовать частоты от соседних налагающихся спектров 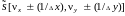(рис. 1.9 б). В результате переналожения спектров возникают так называемые шумы дискретизации.

1.7.4. Теорема Котельникова в частотной области

Пусть оптический сигнал s (x, у) отличен от нуля в прямоугольной области

.

Тогда ПЧС финитного сигнала полностью определяется сово­купностью отсчетов, взятых через одинаковые интервалы , так что по аналогии с (1.64) запишем ряд Котельникова в частотной области в виде

.

Для ЧВС финитного импульса, отличного от нуля на временном интервале , получим

.

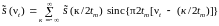Глава 2

Преобразование регулярных сигналов

оптической системой

2.1. Обобщённая оптическая система

2.1.1. Внутренняя структурная модель ООС

Обобщённая оптическая система (рис. 1.3) преобразует входные сигналы s (P) в выходные (преобразованные) оптические сигналы σ(Q), где точка Р (х,у) принадлежит пространству входных сигналов, Q(х',у') – пространству преобразованных сигналов, и её ВншСМ (1.6) определяется прежде всего унарным отношением «быть ООС» в виде на множестве

(2.1) и формально заданным оператором поведения , так что с учётом (1.39)

σ(Q) = P_ООС {s(P)}. (2.2)

Переход от ВншСМ ООС (1.6) к её ВнтрСМ в виде (1.7) осуществляется (рис. 2.1) путем введения тернарного отношения (1.13) и идентификации её поведения с помощью композиции [см. (1.8)] трёх формально заданных преобразующих операторов

. (2.3)

Иначе говоря, преобразующие свойства ООС определяются поведенческими свойствами оптического преобразующего элемента , а также слоёв пространства входных и преобразованных сигналов, которые обладают как осевой, так и сдвиговой симметрией. Явный вид результирующего оператора поведения P_ООС(s | Q,G) существенно зависит от выбранных МП всех ПЭ и от соответствующих значений их внешних Q и внутренних G параметров. На рис. 2.1 идентифицированы виды ОптчПЭ, однако основным преобразующим элементом на практике является объектив (обв). В этом случае с учётом поведенческих свойств объектива P_обв формула (2.3) принимает вид

. (2.3')

При этом главными внутренними параметрами, определяющими поведение ООС, являются толщина – а СП входных сигналов и толщина а_нбл СП преобразованных сигналов. В зависимости от их значений в рамках ВнтрСМ выделяют две основные разновидности ООС, а именно оптическую фурье-преобразующую систему (п. 2.4) и оптическую изображающую систему (п. 2.5).

Дальнейшее исследование ППС в ООС сводится к анализу пространственно-координатного и пространственно-частотного поведения этих частных случаев. При этом конкретный вид как структурной связности R_Σ , так и функционально-преобразующей связности, устанавливаемой МП ПЭ, существенно зависит от степени когерентности излучения, рассеянного объектом [3, 11, 28, 31].