2.2.4. Фраунгоферовский слой пространства

Если расстояние наблюдения удовлетворяет условию Фраунгофера

или ,

то СП называется фраунгоферовским. Тогда в (2.31) 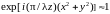и распределение комплексной амплитуды поля, описывающее фраунгоферовское дифракционное изображение, с учетом (2.32) имеет вид

(2.40)

или (2.41)

В результате оператор , задающий пространственно-частотную фраунгоферовскую ВншЛАлгртмМ (2.15) с точностью до функции Френеля совпадает с фурье-оператором F для пространственных частот ν_x = x'/ λ z , ν_y = y'/ λ z, так что

(2.42)

представляет собой разновидность F-МП (2.75) для фраунгоферовского СП как ОФПС ( ). Модуль фраунгоферовского дифракционного изображения

Фурье-образ 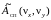в (2.41) можно рассматривать как сумму плоских волн , заданных в плоскости 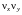и распространяющихся в направлении, которое для малых углов задается вектором . Поэтому дифракцию Фраунгофера называют также дифракцией плоских волн.

Конкретную оценку нижней границы фраунгоферовского СП получим, используя критерий Релея 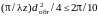, откуда

(2.43)

Так как диаметры областей D_обт и D_U близки друг к другу (рис. 2.3), то из (2.36) и (2.43) следует, что при таком расстоянии наблюдения , что , т.е. угловой размер объекта не превышает .

Пример 2.3. При d_обт = 4 мм и λ = 0,5 мкм френелевский СП шире фраунгоферовского СП. Условие (2.43) имеет глубокий оптико-физический смысл. Из него следует, что фраунгоферовская F-МП (2.42) справедлива величина м, а при d_обт = 32 мм возрастает до км.

Пусть диаметр d_нбл области наблюдения D_нбл также мал

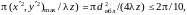
откуда или . (2.44)

Если дополнительно толщина СП , т. е. угловой размер области наблюдения не превышает , то взятая в плоскости наблюдения функция Френеля . Тогда фраунгоферовские дифракционные изображения (2.40) и (2.41) в малой области наблюдения пропорционально фурье-образу входного сигнала, так что

(2.45)

или 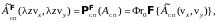(2.46)

где коэффициент пропорциональности не зависит от координат х' и у'. Таким образом, при выполнении условия (2.44) оператор , задающий фраунгоферовскую F-МП (2.42), уже c точностью до постоянного комплексного множителя Фr₀, совпадает с фурье-оператором F для пространственных частот ν_x = x'/λ z , ν_y = y'/λ z. При этом выражения (2.45) и (2.46) фактически описывают дифракционное фурье-изображение.

Так как плоские волны фокусируются в задней фокальной плоскости объектива, то последняя играет роль частотной плоскости. Поэтому на практике для реализации дифракции Фраунгофера и осуществления преобразования Фурье используют высоко корригированный объектив (п. 2.4).

2.2.5. Геометрооптический слой пространства

Найдем распределение комплексной амплитуды на небольшом расстоянии z от плоскости объекта ху в приближении геометрооптической тени. В таком случае говорят о геометрооптическом СП, поведение которого удобно проанализировать, рассматривая его как ПЧФ в рамках общей частотной ВншЛАнлтчМ (2.17) с учетом (2.18) и (2.19), так что

Откуда, используя (2.37) и ограничиваясь первым членом,

Полученное выражение пропорционально обратному преобразованию Фурье от спектральной плотности входного сигнала, так что

(2.47)

Таким образом, дифракционное рассеяние геометрооптического СП настолько мало, что не сказывается даже на самой мелкой неоднородности поля. Дифракционное изображение представляет собой геометрооптическое теневое изображение объекта. Соответствующая ВншЛАнлтчМ геометрооптического СП, называемая геометрооптической МП (ГмоМ), имеет вид

(2.48)

Она является частным случаем ТрМ (2.55) с фазовым коэффициен­том пропускания , который характеризует постоянный набег фазы при распространении волны от плоскости объекта до плоскости наблюдения.

Для оценки верхней границы геометрооптического СП в соответствии с критерием Релея из (2.37) с учетом (2.18) получим

откуда .

Пример 2.4. При δ = 1 мм ( мм ^-1) и λ = 0,5 мкм величина мм, а при

δ = 0,01 мм ( мм ^-1) уменьшается до мм.

Геометрооптическая модель (ГмоМ) (2.48) представляет собой предельный случай ВншЛАнлтчМ френелевского СП (2.33) как ПЧФ при z → 0 в подынтегральном выражении. Действительно, нетрудно видеть, что из (2.34) получим выражение

которое в этом случае превращается в (2.47), т. е. 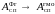. Однако такой переход не дает количественной оценки для толщины геометрооптического СП.