
- •Глава 1 модельное представление процесса преобразования сигналов в оптико - электронных системах
- •1.1. Элементы теории систем
- •1.1.1. Сведения о процессе преобразования сигналов
- •1.1.2. Система
- •1.1.3. Связность сигналов и элементов в ОиЛзЭс
- •1.1.4. Модели системы
- •1.2. Математическое моделирование ОиЛзЭс
- •1.2.1. Математическая модель (мм)
- •1.2.2. Проблемы математической теории ОиЛзЭс
- •1.3. Основные математические модели ОиЛзЭс
- •1.3.1. Постановка задачи моделирования
- •1.3.2. Внешняя и внутренняя мм ОиЛзЭс
- •1.3.3. Структурная модель и модель поведения ОиЛзЭс
- •1.3.4. Связный граф системы моделей над ОиЛзЭс
- •1.3.5. Модель поведения мп
- •1.3.6. Цепи связного графа системы моделей для ОиЛзЭс
- •1.4. Оптико- и лазерно- электронная система
- •1.4.1. Структурная схема ОиЛзЭс
- •1.4.2. Классификация ОиЛзЭс
- •1.5. Плоские и сферические волны
- •1.5.1. Скалярные монохроматические волны
- •1.5.2. Интенсивность монохроматической волны
- •1.5.3.Однородные плоские монохроматические волны
- •1.5.4. Однородные сферические монохроматические волны
- •1.6. Модельное представление линейной ОиЛзЭс
- •1.6.1. Внешняя линейная мп ОиЛзЭс
- •1.6.2. Базисные типовые сигналы
- •1.6.3. Координатная интегральная ВншАлгтмМ линейной ос
- •1.6.4. Координатная SvM пространственно-инвариантной оИзС
- •1.6.5. Частотная линейная АнлтМ пространственно-инвариантной оИзС
- •1.6.6. Модели поведения линейной электронной системы
- •1.7. Дискретно-выборочное представление сигналов с финитным спектром
- •1.7.1. Теорема Котельникова (Уиттекера-Шеннона)
- •1.7.2. Свойства выборочной функции
- •1.7.3. Переналожение спектров
- •1.7.4. Теорема Котельникова в частотной области
- •2.1.2. Когерентная оптическая система
- •2.1.3. Частично когерентная оптическая система
- •2.1.4. Некогерентная оптическая система
- •2.2. Преобразование оптических сигналов слоем пространства
- •2.2.1. Принцип Гюйгенса-Френеля
- •2.2.2. Внешние линейные модели поведения слоя пространства
- •2.2.3. Френелевский слой пространства (Фr-сп)
- •2.2.4. Фраунгоферовский слой пространства
- •2.2.5. Геометрооптический слой пространства
- •2.3. Транспарантная модель поведения тонкого однолинзового объектива
- •2.3.1. Коэффициент пропускания и отражения в транспарантном представлении
- •2.3.2. ТрМ оптического модулирующего объекта
- •2.3.3. Комплексный амплитудный коэффициент пропускания тонкого однолинзового анаберрационного сферического объектива в приближении дос
- •2.3.4. Оптико-физический смысл тонкого однолинзового анаберационного объектива
- •2.4. Оптическая фурье-преобразующая система
- •2.4.1. Координатная ВнтрСм офпс с транспарантным входом
- •2.4.3. Координатная ВнтрСм офпс с линзовым входом
- •2.5. Когерентная оптическая изображающая система
- •2.5.1. ГрфМ иерархической структуры оос.
- •2.5.2. Пространственно-координатные мп когерентной оИзС в приближении дос.
- •2.5.3. SvM когерентной ОизС в приближении рос, КрпДос, адос и иос
- •2.5.4. Частотная лАнлтчМ когерентной пиоИзС
- •2.5.5. Модели поведения частично когерентной пиоИзС
- •2.6. Некогерентная оптическая изображающая система
- •2.6.1. SvM некогерентной оИзС
- •2.6.2. Частотная лАнлтчМ некогерентной пиоИзС
- •2.6.3.Свойства опф
- •2.6.4. Передача пространственных частот в некогерентной пиоИзС
- •2.6.5. Величина потока излучения в некогерентном изображении точечного источника
- •2.6.6. Модельные представления опф
- •2.6.6.1. Автоковариационная модель (аKvM) опф
- •2.6.6.2. Геометроаналитическая модель (ГмаМ) опф КрпДос
- •2.6.7. Аппроксимирующая см нкфр
- •2.7. Влияние монохроматических аберраций на передаточные функции оптической изображающей системы
- •2.7.1. Волновая аберрация
- •2.7.2. Связь между волновыми и геометрооптическими аберрациями
- •2.7.3. Влияние монохроматических аберраций на кпф
- •2.7.4. Влияние монохроматических аберраций на опф
- •2.7.5. Влияние функции зрачка на опф
- •2.7.6. Влияние волновой аберрации на опф
- •2.8. Голографическая изображающая система
- •2.8.1. ВнтрСм голографического процесса
- •2.8.1. ВнтрСм типа голограммы.
- •2.8.2. Пространственно-частотная ТрМ двумерной коголограммы.
- •2.8.4. Восстановление волнового фронта с помощью двумерной пропускающей амплитудной коголограммы
- •3.2. Пространственная передаточная функция маи
- •3.2.2. ЛАнлтМп маи и определение ппф
- •3.2.3. Определение ппф маи с плоской симметрией в декартовой системе координат
- •3.2.4. Ппф осесимметричного маи
- •3.2.5. Ппф осесимметричного маи с учетом угловой периодичности растра
- •3.3. Частотно-временной спектр потока излучения на выходе маи
- •3.3.1 Временной поток излучения на выходе маи (Шатоха)
- •3.3.2. Поступательное движение маи
- •3.3.2.1. Поступательное движение вдоль прямолинейной траектории
- •3.3.2.2. Линейное сканирование маи вдоль оси оX
- •3.3.3. Круговое сканирование маи
- •3.3.4. Вращательное сканирование маи вокруг собственной оси
- •3.3.4.1. Получастотный метод
- •3.3.4.2. Частотный метод
- •3.4. Преобразование оптического сигнала приемником излучения (Шатоха)
- •3.4.1. Энергетические характеристики чувствительности пи
- •3.4.2. Частотно-временные характеристики пи
- •3.4.3 Неоднородность чувствительности пи
- •3.4.4. Полная передаточная функция пи
- •3.4.5. Чвс на выходе пи. Квазимонохроматический поток
- •3.4.6. Чвс на выходе пи. Полихроматический поток
- •3.4.7. Полихроматическая пф КмпзцСист:
- •3.5. Преобразование сигнала электронным трактом
- •3.5.1. Дифференцирование и интегрирование сигналов
- •3.5.2. Нелинейное преобразование сигналов
- •3.5.3. Амплитудное детектирование
- •3.5.4. Частотное и фазовое детектирование
- •3.5.5. Примеры структурных схем электронного тракта оэс
- •3.5.6. Развертка и восстановление изображения
- •Глава 4 преобразование случайных сигналов в оптико и лазерно-электронных системах
- •4.1. Преобразование случайных сигналов
- •Линейными и нелинейными элементами
- •4.1.1. Постановка задачи
- •4.1.1.1. Корреляционный метод расчёта
- •4.1.1.2. Частотный метод расчёта
- •4.1.2. Преобразование случайного сигнала нелинейной системой
- •4.1.3. Преобразование плотности вероятности
- •4.1.4. Корреляционная функция и спектральная плотность на выходе нбэ
- •4.2. Преобразование случайного поля яркости оптической изображающей системой
- •4.2.1. Яркостные характеристики естественных фонов
- •4.2.1.1. Фоновые образования с протяжёнными резкими перепадами яркости
- •4.2.1.2. Спектральная плотность корреляционной функции случайного яркостного фонового поля
- •4.2.3. Преобразование фонового излучения оптической системой
- •4.2.3.2. Частотный метод расчёта
- •4.2.3.3. Частотный и Kr-методы расчёта для удалённого объекта
- •4.3. Преобразование случайного оптического сигнала маи
- •4.3.1. Преобразование фонового потока излучения неподвижным маи
- •4.3.1.2. Частотный метод расчёта
- •4.3.2. Преобразование фонового потока излучения подвижным маи
- •4.3.3. Поступательное движение маи
- •4.3.4. Вращательное сканирование маи вокруг собственной оси
- •4.4. Преобразование случайного оптического сигнала приёмником излучения и электронным трактом
- •4.4.1. Преобразование случайного сигнала пи
- •4.4.2. Преобразование случайного сигнала эт
- •4.5. Отношение сигнал/помеха на выходе линейной инвариантной во времени ОиЛзЭс
- •4.5.1. Постановка задачи
- •4.5.2. Определение осп на выходе линейной инвариантной оэс
- •4.5.3. Осп при линейном сканировании
- •Глава 5. Обнаружение оптических сигналов и измерение их параметров
- •5.1. Три варианта общей постановки задачи
- •(Назначение, цель, исходные данные)
- •5.1.1. Задача обнаружения оптического объекта
- •5.1.2. Задача измерения
- •5.1.3. Задача воспроизведения
- •5.1.4. Вывод
- •5.2. Вероятностные характеристики обнаружения
- •5.2.1. Априорные и апостериорные вероятности обнаружения
- •5.3. Критерии, лежащие в основе принятия решения системой (критерии обнаружения основаны на выборе )
- •5.3.1. Критерий максимума апостериорной условной вероятности,
- •5.3.2. Критерий минимального среднего риска (Критерий Кр 2° Байеса)
- •5.3.3. Критерий максимума правдоподобия (Кр 3°)
- •5.3.4. Критерий Неймана-Пирсона
- •5.4. Обнаружение методом однократного отсчёта
- •5.4.1. Постановка задачи
- •5.4.2. Описание метода однократного отсчёта
- •5.4.3. Недостатки метода однократного отсчёта
- •5.4.3.1. Метод непрерывного сравнения мгновенного значения
- •5.4.3.2. Определение значения в момент отсчёта
- •5.4.4. Вероятностные характеристики обнаружения в методе непрерывного сравнения мгновенных значений реализации с
- •5.4.4.1 Условная вероятность ложной тревоги
- •5.4.4.2 Условная вероятность пропуска объекта
- •5.4.5. Отношение сигнал/помеха. Рабочие характеристики ОиЛзЭс
- •5.4.5.1. Рабочие характеристики ОиЛзЭс обнаружения на основе Кр4º (Неймана-Пирсона)
- •5.4.5.2. Рабочие характеристики ОиЛзЭс обнаружения на основе Кр1º (Котельникова или максимума апостериорной вероятности) и Кр2º (Байеса или минимума среднего риска)
- •5.4.6. Расчет вероятности возникновения ложной тревоги
- •5.4.7. Рабочие характеристики обнаружения
- •5.5. Корреляционный метод обнаружения
- •5.5.0. Постановка задачи
- •5.5.1. Выборка конечного объёма
- •5.5.1.1. Первый алгоритм обнаружения
- •5.5.1.2. Второй алгоритм обнаружения
- •5.5.2. Выборка бесконечного объёма
- •5.5.3. Вероятностные характеристики обнаружения на основе корреляционного метода
- •5.5.4. Преимущества и недостатки Kr-метода
- •5.5.4.1. Преимущества Kr-метода
- •5.5.4.2. Недостатки Kr-метода
- •5.5.4. Практическая реализация корреляционного метода обнаружения
- •5.6. Обнаружение с использованием оптимальной фильтрации
- •5.6.1. Электронная система обнаружения на основе чвф
- •5.6.2. Оценка мгновенного значения осп на выходе чвф
- •5.6.3. Структурная схема оптимального чвф
- •5.6.3.1. Свойства оптимального чвф
- •5.6.3.2. Синтез структурной схемы оптимального чвф
- •5.6.4. Анализ оптимального отношения сигнал/помеха
- •5.6.5. Оптимальная фильтрация в оИзС
- •5.6.6. Трехмерный оптимальный пространственно-временной
- •5.6.7. Оптическая согласованная фильтрация в системе
- •5.7. Статистическая оценка измеряемых параметров сигнала
- •5.7.1. Задача измерения параметров сигнала при наличии помех
- •5.7.2. Нахождение
- •5.8. Функция потерь и эффективность правил оценки
- •5.8.1. Функция потерь как характеристика погрешностей измеренного параметра
- •5.8.2. Байесовская оценка измеряемого параметра
- •5.8.3. Эффективность байесовской оценки
- •5.8.3.2. Функция потерь, линейная по модулю
- •5.8.3.3. Квадратичная функция потерь
- •5.8.3.4. Прямоугольная функция потерь
- •5.8.4. Выводы
- •5.9. Оценка измеряемых сигнальных параметров при аддитивных помехах с нормальным распределением
- •5.9.1. Измерение произвольного параметра
- •5.9.2. ОиЛзЭс измерения амплитуды (пикового значения) сигнала
- •5.9.3. Статистические характеристики оптимальной оценки
- •5.9.3.1. Математическое ожидание случайной оптимальной оценки
- •5.9.3.2. Дисперсия случайной оптимальной оценки измеряемой амплитуды а
- •5.9.4. Аналогия между задачами обнаружения объекта
- •Глава 6. Методика и примеры светоэнергетического расчета оэс
- •6.1. Методика расчета оэс в режиме обнаружения
- •6.1.1. Требуемое , реализуемое осп
- •6.1.2. Энергетический расчет сканирующей оэс со строчно-кадровой разверткой
- •6.2. Расчет сканирующей оэс в режиме обнаружения
- •6.3. Расчет оэс измерения дефокусировки объективов
- •Последовательность расчета в случае амплитудного метода измерения продольной дефокусировки
- •Последовательность расчета в случае фазового метода измерения продольной дефокусировки
- •Последовательность расчета в случае амплитудного метода измерения продольной дефокусировки
- •Последовательность расчета в случае фазового метода измерения продольной дефокусировки
1.5.3.Однородные плоские монохроматические волны
Любое решение волнового уравнения (1.14) вида
 (1.23)
(1.23)
представляет собой
плоскую
волну,
так как в
каждый момент времени
 величина
величина
 постоянна во всех
точках плоскости, задаваемой векторным
уравнением в виде скалярного произведения
постоянна во всех
точках плоскости, задаваемой векторным
уравнением в виде скалярного произведения
 ,
,
где
 –
радиус-вектор точки
–
радиус-вектор точки
 ;
;
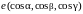 –
единичный вектор нормали к плоскости,
координаты которого определяются
направляющими косинусами (рис. 1.4). Иначе
говоря, плоская волна, фаза которой
постоянна во всех точках некоторой
плоскости, имеет плоский
волновой фронт.
–
единичный вектор нормали к плоскости,
координаты которого определяются
направляющими косинусами (рис. 1.4). Иначе
говоря, плоская волна, фаза которой
постоянна во всех точках некоторой
плоскости, имеет плоский
волновой фронт.
Общее
решение волнового уравнения (1.14)
в виде (1.23),
выражающее плоскую волну, которая
распространяется в направлении вектора
 со скоростью
со скоростью
 ,
имеет вид
,
имеет вид
 (1.24)
(1.24)
Аргумент функции
 не меняется при замене величин
не меняется при замене величин
 и t
на величины
и t
на величины
 и
и
 соответственно.
Физически это означает, что возмущение
,
которое в момент времени t
было в
плоскости, находящейся на расстоянии
d
от начала
координат, в более поздний момент времени
оказывается в
плоскости, расположенной уже на расстоянии
от начала координат.
Вводя в (1.17)
в результате
замены t
нa
соответственно.
Физически это означает, что возмущение
,
которое в момент времени t
было в
плоскости, находящейся на расстоянии
d
от начала
координат, в более поздний момент времени
оказывается в
плоскости, расположенной уже на расстоянии
от начала координат.
Вводя в (1.17)
в результате
замены t
нa
 структуру плоского
волнового фронта и учитывая, что для
однородной плоской волны
структуру плоского
волнового фронта и учитывая, что для
однородной плоской волны
 ,
получим скалярное комплексное выражение
для электрического (магнитного)
поля однородной
плоской монохроматической волны
,
получим скалярное комплексное выражение
для электрического (магнитного)
поля однородной
плоской монохроматической волны
 (1.25)
(1.25)
где
 ;
;
 –
длина волны
в среде с
показателем преломления n.
Длину волны
–
длина волны
в среде с
показателем преломления n.
Длину волны
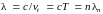 (1.26)
(1.26)
называют приведенной
длиной волны
(соответствует
распространяющейся в вакууме
монохроматической волне той же частоты).
Вектор
 или
или
 для вакуума
для вакуума
 ,
,

направленный вдоль
единичного вектора нормали (рис. 1.4),
называют волновым
вектором.
Его длину
,
соответственно для вакуума
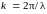 ,
называют волновым
числом.
Волновой
вектор является обобщенным пространственным
аналогом временной угловой частоты
,
называют волновым
числом.
Волновой
вектор является обобщенным пространственным
аналогом временной угловой частоты
 .
.
Так
как выражение (1.25)
не изменяется
при замене
на
 то
то
 ,
является пространственным периодом
плоской волны. Для задания ориентации
пространственных гармонических
осцилляции в плоской волне на практике
очень удобно ввести векторы
пространственной частоты
,
является пространственным периодом
плоской волны. Для задания ориентации
пространственных гармонических
осцилляции в плоской волне на практике
очень удобно ввести векторы
пространственной частоты
 ,
,
 ,
(1.27)
,
(1.27)
направления которых совпадают с направлением распространения , а длины соответственно равны
 ,
,
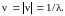 (1.28)
(1.28)
Они задают число
пространственных периодов (осцилляций)
в волне, укладывающихся на единице
длины, 1/мм, соответственно в среде или
в вакууме, и по аналогии с временной
частотой
 называются
пространственными
частотами.
Это еще более
углубляет аналогию между волновым
вектором
называются
пространственными
частотами.
Это еще более
углубляет аналогию между волновым
вектором
 и угловой частотой
и угловой частотой
 .
.
В итоге комплексную амплитуду однородной плоской монохроматической волны можно представить в виде
 (1.29)
(1.29)
 (1.30)
(1.30)
В
(1.30) в соответствии с (1.24) фаза
 увеличивается
с ростом расстояния d
от начала
координат, а фаза
увеличивается
с ростом расстояния d
от начала
координат, а фаза
 уменьшается
с ростом времени t.
Выбор такого
правила знаков в плоской волне обусловлен
описанием ее распространения в направлении
вектора
.
Он не имеет
существенного значения, так как
практический интерес представляет не
абсолютная величина фазы, а разность
фаз. В то же время в рамках выбранного
правила знаков процесс распространения
плоской волны сводится к следующему.
Для любой точки некоторой плоскости
согласно (1.30) полная
фаза волны в момент времени t
постоянна
и равна
уменьшается
с ростом времени t.
Выбор такого
правила знаков в плоской волне обусловлен
описанием ее распространения в направлении
вектора
.
Он не имеет
существенного значения, так как
практический интерес представляет не
абсолютная величина фазы, а разность
фаз. В то же время в рамках выбранного
правила знаков процесс распространения
плоской волны сводится к следующему.
Для любой точки некоторой плоскости
согласно (1.30) полная
фаза волны в момент времени t
постоянна
и равна
 .
В более
поздний момент времени
полная фаза будет
иметь то же значение на большем расстоянии
от начала координат
.
В более
поздний момент времени
полная фаза будет
иметь то же значение на большем расстоянии
от начала координат
 ,
так как
,
так как
 ,
в то время
как на прежнем расстоянии d
она уменьшается.
В результате плоский волновой фронт
перемещается в пространстве в направлении,
которое в зависимости от специфики
задачи можно охарактеризовать одним
из трех коллинеарных векторов –
единичным вектором нормали
,
вектором
пространственной частоты
,
в то время
как на прежнем расстоянии d
она уменьшается.
В результате плоский волновой фронт
перемещается в пространстве в направлении,
которое в зависимости от специфики
задачи можно охарактеризовать одним
из трех коллинеарных векторов –
единичным вектором нормали
,
вектором
пространственной частоты
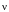 или волновым вектором
(рис. 1.4).
или волновым вектором
(рис. 1.4).
Таким образом, однородная плоская монохроматическая волна (1.30) является тем важным частным случаем комплексного временного гармонического сигнала (1.17), который позволяет с единых позиций рассматривать частотно-временные и пространственно-частотные гармонические осцилляции произвольной монохроматической электромагнитной волны, представляемой в виде суммы плоских волн. Это в свою очередь служит первым шагом на пути создания общей частотной МП ОЭС при описании множества S входных сигналов набором плоских волн.
Для
описания плоской волны, распространяющейся
в противоположном направлении, надо во
всех полученных выражениях
заменить векторы
 на противоположные
на противоположные
 .
.
Тогда на основании (1.29) комплексная амплитуда примет вид

Нетрудно
видеть, что противоположному направлению
распространения соответствует
комплексно-сопряженная амплитуда. В
этом, в частности, проявляется одно из
преимуществ введения комплексного
оптического сигнала. Другое преимущество
использования комплексной амплитуды
выясняется при переходе к координатному
представлению однородной плоской
монохроматической волны. Вектор
пространственной частоты
 перпендикулярен
трехмерной плоскостной периодической
решетке, состоящей, например, из максимумов
пространственно-частотной гармоники,
которая соответствует комплексной
амплитуде плоской волны в фиксированный
момент времени и тем самым задает ее
ориентацию. На рис. 1.5 приведена решетка
с вектором
,
лежащим в плоскости хz,
так что ее
реберные грани перпендикулярны этой
плоскости (параллельны оси у).
С учетом
(1.27) координаты
перпендикулярен
трехмерной плоскостной периодической
решетке, состоящей, например, из максимумов
пространственно-частотной гармоники,
которая соответствует комплексной
амплитуде плоской волны в фиксированный
момент времени и тем самым задает ее
ориентацию. На рис. 1.5 приведена решетка
с вектором
,
лежащим в плоскости хz,
так что ее
реберные грани перпендикулярны этой
плоскости (параллельны оси у).
С учетом
(1.27) координаты
 ,
,
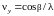 ,
,
 (1.31)
(1.31)
называют координатными
пространственными частотами соответственно
вдоль осей х,
у, z.
Если
направление распространения
(или
)
составляет
с какой-либо осью угол меньше 90°, то
соответствующая координатная
пространственная частота положительна.
Если угол больше 90°,
то частота
отрицательна. В оптике координатные
пространственные частоты часто выражаются
через дополнительные углы (углы
падения)
 ,
,
 ,
, ,
так что
,
так что
 ,
,
 ,
,
 .
Тогда,
переходя в (1.29) к координатной форме
записи скалярного произведения
.
Тогда,
переходя в (1.29) к координатной форме
записи скалярного произведения
 ,
получим
,
получим
 (1.32)
(1.32)
В частности, плоская волна, распространяющаяся в направлении
 ,
параллельном плоскости хz
(
,
параллельном плоскости хz
( =
90°, рис. 1.5), имеет в произвольной точке
комплексную
амплитуду
=
90°, рис. 1.5), имеет в произвольной точке
комплексную
амплитуду

При
 получим выражение
для комплексной амплитуды в точке
получим выражение
для комплексной амплитуды в точке
 плоскости х0у
плоскости х0у
 .
.
Наконец, если
 (
( ),
то комплексная амплитуда плоской волны,
распространяющейся в направлении оси
),
то комплексная амплитуда плоской волны,
распространяющейся в направлении оси
 ,
в точке
,
в точке
 имеет вид
имеет вид
 ,
,
а в точке
 она будет
она будет
 .
.
Оптико-физический
смысл координатных пространственных
частот заключается в том, что их знаки
определяют направление распространения
плоской волны, а численные значения
обратно пропорциональны пространственным
периодам
 ,
,
 ,
,
 трехмерной
плоскостной решетки вдоль соответствующих
координатных осей
трехмерной
плоскостной решетки вдоль соответствующих
координатных осей
 ,
,
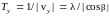 ,
,
 .
.
Для волны,
распространяющейся в направлении
(рис. 1.5) с вектором
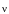 ,
лежащим в I
квадранте, частоты
,
лежащим в I
квадранте, частоты
 ,
,
 ,
,
 ,
так что
,
так что
 ,
,
 ,
,
 .
.
В этом случае
и
определяют пространственные периоды
плоских решеток, которые получаются в
сечениях трехмерной решетки плоскостями
ху и
zу.
Для II
квадранта
,
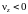 ,
для III
квадранта
,
для III
квадранта
 ,
,
а для IV
,
.
,
,
а для IV
,
.
На основании (1.28) и (1.31) координатные пространственные частоты в плоской волне связаны соотношением
 ,
,
откуда
 ,
где знак определяется знаком
,
где знак определяется знаком
 .
Тогда
согласно (1.32) можно описать процесс
распространения комплексной амплитуды
плоской волны в пространстве, если
выразить
.
Тогда
согласно (1.32) можно описать процесс
распространения комплексной амплитуды
плоской волны в пространстве, если
выразить
 через
через
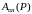

где
 .
В
результате комплексная амплитуда
плоской волны
на произвольном
расстоянии
от начала
координат оказывается равной
произведению комплексной амплитуды
в плоскости ху
на комплексную
экспоненциальную функцию распространения
[см. (2.18)]
.
В
результате комплексная амплитуда
плоской волны
на произвольном
расстоянии
от начала
координат оказывается равной
произведению комплексной амплитуды
в плоскости ху
на комплексную
экспоненциальную функцию распространения
[см. (2.18)]
 (1.33)
(1.33)
описывающую фазовую пространственно-частотную дисперсию. В соответствии с выбранным правилом знаков с ростом фаза волны увеличивается. Как показано в 2.2.2 (см. 2.18) это выражение идентифицирует когерентную передаточную функцию когерентного слоя свободного пространства.
Однородная плоская монохроматическая волна является одним из основных типовых оптических сигналов СП. Сдвиговая симметрия плоской волны естественным образом совпадает со сдвиговой симметрией однородного СП, ибо при любом сдвиге в плоскости, совпадающей с волновым фронтом, комплексная амплитуда плоской волны не меняется. Поэтому описание ее распространения лежит в основе пространственно-частотной ВншМП СП.
