3.2.3. Определение ппф маи с плоской симметрией в декартовой системе координат

Очень часто МАИ состоят из простых или повторяющихся элементов, поэтому при нахождении их ППФ используют теоремы линейности и смещения преобразования Фурье. Предположение о линейности пространственных фильтров МАИ основано на том, что реакция на сумму входных сигналов равна сумме реакции на каждый сигнал в отдельности.

1) На рис. 3.3 показана часть МАИ, состоящего из однотипных пропускающих элементов. Функция пропускания нулевого элемента равна , а к-го элемента может быть выражена через как , где — координаты центра пропускающего элемента.

Функция пропускания всего МАИ может быть записана в виде

(3.5)

где N — число прозрачных элементов.

Преобразование Фурье нулевого элемента

Соответственно преобразование Фурье от к-го элемента с использованием теоремы смещения

(3.6)

Взяв преобразование Фурье от (3.5) с учетом зависимости (3.6), получим ППФ МАИ

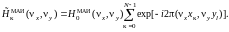(3.7)

Для некоторых конкретных видов МАИ, например для МАИ, показанном на рис. 3.3, можно получить более удобную формулу для определения ППФ, чем (3.7). Функцию пропускания МАИ, показанную на рис. 3.3, можно записать в следующем виде:

Если , то

Взяв от преобразование Фурье, получим

(3.7')

3.2.4. Ппф осесимметричного маи

2) Далее найдем ППФ МАИ, имеющего осевую симметрию (рис. 3.4), которую удобнее находить в полярной системе координат. Функция пропускания к-го элемента может быть выражена через функцию пропускания нулевого элемента как .

Функция пропускания всего МАИ, состоящего из N однотипных элементов, для усилит…

(3.8)

Запишем преобразование Фурье от функции пропускания нулевого элемента в полярной системе координат

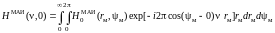(3.9)

Преобразование Фурье от функции пропускания к-го элемента

Проведя замену переменной , и учитывая периодичность функции , для получим

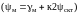
(3.10)

Из сравнения (3.9) и (3.10) имеем

(3.11)

Таким образом, ППФ к-го элемента получается путем поворота ППФ нулевого элемента в частотной области на угол , аналогичного повороту функции пропускания l-го элемента в пространстве координат . Взяв преобразование Фурье от (3.8) с учетом зависимости (3.11), получим ППФ МАИ

(3.12)

3.2.5. Ппф осесимметричного маи с учетом угловой периодичности растра

2) Для определения ППФ МАИ в полярной системе координат, кроме (3.12), можно получить другое выражение, которое учитывает периодический характер структуры МАИ и в некоторых практических случаях оказывается более удобным. Преобразование Фурье от функции пропускания МАИ в полярной системе координат можно записать в следующем виде:

(3.13)

Так как – периодическая функция относительно переменной c периодом , то ее можно разложить в ряд Фурье:

(3.14)

где – комплексная амплитуда угловой ПЧ гармоники в кольце радиуса шириной .

Подставляя (3.14) в (3.13) и меняя местами операции суммирования и интегрирования, получим

(3.15)

Рассмотрим внутренний интеграл в выражении (3.15). Вводя новую переменную , так что , и учитывая, что экспонента имеет период по аргументу , после несложных преобразований запишем

где - функция Бесселя первого рода n-го порядка, .

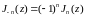ППФ МАИ в полярной системе координат может быть также представлена в виде ряда Фурье по пространственно-частотному углу , т. е.

(3.16)

где ()

Зависимость (3.16) удобнее для определения ППФ МАИ вращающегося вокруг своей оси.

Рассмотрим обратную задачу – нахождение функции пропускания МАИ по его ППФ. Обратное преобразование Фурье для МАИ в полярной системе координат

(3.17)

Так как – функция периодическая по переменной  с периодом , то она раскладывается в ряд Фурье (3.16). Подставляя (3.16) в (3.17) и проведя преобразования, аналогичные (3.14) – (3.15'), получим

(3.16')

где

Рассмотрим примеры определения ППФ МАИ.

Пример 3.1. На рис. 3.5 показан МАИ с шахматным расположением пропускающих и непрозрачных элементов. Функция пропускания нулевого элемента .

Преобразование Фурье от функции равно

(3.18)

Пропускающие элементы смещены вдоль оси относительно нулевого на расстояние к2а, где к = 0, 1, 2, ..., М – 1, поэтому в соответствии с формулой (3.10) преобразование Фурье пропускания первого горизонтального ряда определяется зависимостью

где М – число прозрачных элементов вдоль оси . Сумма, входящая в , представляет собой сумму членов геометрической прогрессии с первым членом и знаменателем , которая равна

После несложных преобразований для окончательно имеем

(3.19)

Пропускающие элементы второго ряда смещены относительно первого по оси на величину а, а по оси 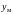– на величину b. Преобразование Фурье функции пропускания двух рядов МАИ можно записать в виде

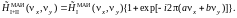
Преобразуем выражение в фигурных скобках

Тогда ППФ двух рядов МАИ

Первые два ряда прозрачных и непрозрачных элементов по оси повторяются с периодом 2b. Следовательно, ППФ всего МАИ

После подстановки значений функции и несложных преобразований получим окончательный вид ППФ МАИ с шахматным расположением прозрачных и непрозрачных элементов:

где 2MNab – площадь пропускающей части МАИ.

Если начало координат поместить в центр МАИ, то экспоненциальный множитель обращается в единицу.

Один квадрант модуля ППФ рассмотренного МАИ показан на рис. 3.6. Максимумы ППФ соответствуют значениям пространственных частот

Передаточная функция МАИ с шахматным распределением пропускающих и непрозрачных элементов очень чувствительна к равномерному распределению потока излучения по всей площади МАИ и к резко выраженным краям образований, расположенных под углом к оси . Если рассмотренный МАИ осуществляет сканирование вдоль оси или , то попадание потока излучения протяженного фона с ярко выраженными краями, параллельными указанным осям, не приводит к модуляции фона.

Пример 3.2. На рис. 3.4 показан секторный МАИ с М числом пар пропускающих и непрозрачных секторов. Для определения ППФ указанного МАИ будем использовать зависимости (3.14) и (3.16). Функция пропускания МАИ может быть записана в следующем виде:

Используя (3.14), определим

После несложных преобразований получим

Выражение в фигурных скобках представляет собой сумму членов геометрической прогрессии, которая равна 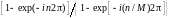, так что

Откуда окончательно, после раскрытия неопределенности,

где

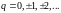
Далее, используя (3.16), найдем . Для n = 0 имеем

, так что по аналогии c примером 2.9

Для (целого и нечетного) имеем

Введя переменную , получим

Используя выражение для интеграла [9] в виде

где Г(x) – гамма функция; – функция Ломмеля, для имеем

В частности, при М = 6 первое отличное от нуля слагаемое в формуле для , определяемое из условия n/М = 1, представляет собой шестую (n = 6) пространственно-частотную угловую гармонику exp(i6) с комплексной амплитудой

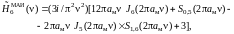
которая зависит от пространственной частоты . При равномерном вращении МАИ с угловой скоростью эта шестая гармоника реализуется в виде первой гармоники временного сигнала с периодом . Нормированные амплитуды нулевой и шестой гармоник показаны на рис. 3.7. Из графика видно, что они имеют явно выраженные максимумы, при при . Таким образом, ППФ секторного МАИ оказывается чувствительной к равномерному фоновому потоку и к изображению синусоидальных объектов, пространственные частоты которых соответствуют максимумам гармонических составляющих и т. д.