2.6.7. Аппроксимирующая см нкфр

При предварительных расчетах для определения приближенного вида ПЧС выходного сигнала в ОЭС, а также для обоснования технических требований к оптической системе, НКФР для средней длины волны рабочего диапазона задается аналитически в виде аппроксимирующей функции. Как следует из п. 1.2, функция двух переменных является частным случаем тернарного отношения в виде Тогда в рамках общего модельного подхода аппроксимация НКФР и ее нормированно-приведенного представления сводится к построению СМ НКФР или для краткости Н-СМ:

Графики наиболее часто встречающихся НКФР, которые опреде­ляют типовые базисные преобразованные -сигналы, приведены на рис.2.19 [28].

Пример 2.8. Прямоугольная НКФР (прямоугольный параллелепипед, рис. 2.19, а) отлична от нуля в прямоугольной области

Соответствующая ОПФ (рис. 2.20,а) как фурье - образ нормировочно -приведенной прямоугольной НКФР имеет вид

Пример 2.9. Круговая НКФР (цилиндр, рис. 2.19, б) отлична от нуля внутри круга

Переходя к нормированно-приведенной круговой НКФР и используя преобразование Фурье-Бесселя (см. П.3.25), получим

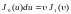Проведя замену с учетом свойства функций Бесселя и , где - функция Бесселя первого рода первого порядка, имеем ОПФ в виде

Функция означает, что ОПФ в случае круговой НКФР порождается функцией Бесселя и имеет вид, подобный (рис. 20, б).

Пример 2.10. Секториальная НКФР (секториальная призма, рис.2.19, в) отлична от нуля в секторе

ОПФ как фурье-образ нормировочно-приведенной векториальной НКФР

где не выражается в квадратурах. На практике ее используют в получастотном методе определения ПЧС сигнала на выходе ОЭС с вращающимся МАИ. Тогда, учитывая периодический характер , ее можно разложить в комплексный ряд Фурье

где

Пример 2.11. Косинусоидальная НКФР m-го порядка (рис. 2.19, г) отлична от нуля в прямоугольной области

Несмотря на то, что отлична от нуля внутри прямо­угольника (квадрата), в окрестности начала координат в случае квадратной области она локально подобна осесимметричной функции. Поэтому обычно на практике р = q, так что нормирующий множитель [см. (2.157)]

где , Г(z) – гамма функция.

Используя представления для Г(z), получим окончательно

где n = 1, 2, ... . Некоторые значения приведены ниже:

n	1	2	3	4	5	6	7	8
	0,25	0,406	0,562	0,722	0,879	1,038	1,195	1,356

Применение косинусоидальной НКФР приводит хотя и к громоздким, но практически всегда выполнимым вычислениям при нахождении ОПФ.

Пример 2.12. Гауссова НКФР (рис. 2.19, 3д) отлична от нуля на всей плоскости и соответственно в декартовой и полярной системах координат имеет вид

где r_д - радиус НКФР, на котором интенсивность падает в е² раз; х_д, у_д - соответствующие размеры вдоль осей х' и у'. В пятне рассеяния радиусом r_д сосредоточено ~ 87 % всей энергии. Соответствующие нормирующие множители имеют вид

Тогда ОПФ тоже оказывается гауссовыми:

График ОПФ показан на рисунке 2.20в.