1.3. Дифференциальные уравнения неразрывности, движения и энергии

Единообразная форма трех законов физики позволяет с помощью теоремы о дивергенции преобразовать интегралы по поверхности к интегралам по объему, а затем по правилу Лейбница о дифференцировании определенных интегралов по параметру поменять последовательность дифференцирования и интегрирования. Полученные уравнения дают возможность записать дифференциальные уравнения неразрывности, движения и энергии пищевой среды, спроектировать эти уравнения на оси координат и решать различные краевые задачи течения, если известны дополнительно реологические уравнения или уравнения состояния дисперсной пищевой среды.

Итак, после названных преобразований законы физики могут быть записаны в виде

; (1.11)

; (1.12)

. (1.13)

В прямоугольных координатах дифференциальный оператор и полный дифференциал определяются равенствами

; (1.14)

, i = 1, 2, 3, (1.15)

где v_i – проекция скорости потока на ось x_i.

Тогда уравнение неразрывности для пищевой среды приобре-тет вид

. (1.16)

Следуя определению полной производной и раскрывая выражение для слагаемого, содержащего дивергенцию, запишем

; (1.17)

в проекциях на прямоугольную систему координат х, у, z

. (1.18)

Аналогично запишем уравнение движения:

. (1.19)

Положительный тензор  соответствует отрицательному гидростатическому давлению р, а давление дает только дополнительный эффект к нормальным силам; это давление можно исключить из тензора напряжений, вычитая р из каждого диагонального члена тензора . Следовательно, можно ввести новый тензор напряжений :

 =  + р, (1.20)

где единичный тензор имеет вид

(1.21)

или

(1.22)

и

. (1.23)

Теперь уравнение движения можно записать следующим образом:

. (1.24)

Проектируя уравнение (1.24) на оси прямоугольных координат х, у, z, получим уравнения движения пищевой среды в скалярной форме:

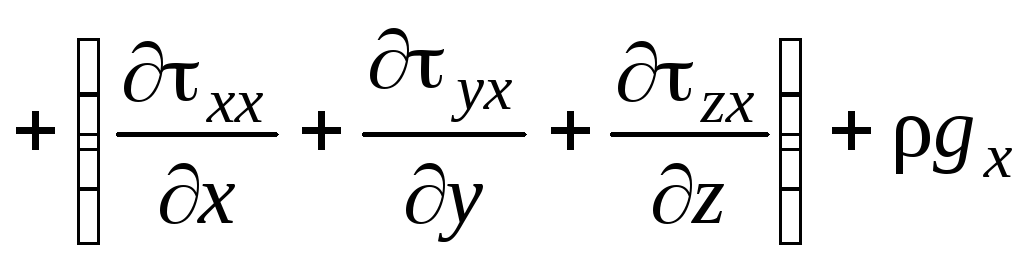; (1.25)

; (1.26)

. (1.27)

После ряда подобных преобразований можно получить уравнение энергии в прямоугольных координатах:

, (1.28)

где А – термический эквивалент работы; с_V – удельная теплоемкость пищевой среды при постоянном объеме.

Тепловой поток связан с градиентом температуры в изотропной среде законом теплопроводности Фурье:

, (1.29)

где  – коэффициент теплопроводности пищевой среды.

Формулы (1.28) и (1.29) позволяют решать термодинамические задачи расчетов переработки пищевых сред.

1.4. Тензор напряжений

В инженерной реологии пищевых дисперсных сред предполагается в основном рассматривать задачи течения, поэтому рассмотрим выражение для поверхностной силы вязкого сопротивления, приходящейся на единицу некоторой площадки, произвольно ориентированной в пространстве в прямоугольной системе координат. Вырежем мысленно элементарный тетраэдр, вершина которого совпадет с началом системы координат (рис. 1.1). Ориентация площадки определяется единичным вектором , скорость течения среды – вектором ; n – расстояние от начала координат до произвольной площадки, до основания тетраэдра.

На рис. 1.1 показаны три напряжения, которые вызваны силами, действующими в направлении оси х₁. Первый индекс указывает на ориентацию поверхности, к которой приложена сила; второй индекс – на направление, вдоль которого действует сила. Например, ₃₁ обозначает тангенциальную силу, отнесенную к единице площади, т. е. напряжение, действующее на грань, перпендикулярную оси х₃ в направлении вдоль оси х₁. Если обозначить площади граней тетраэдра, находящихся в координатных плоскостях, через S₁, S₂, S₃ и стянуть тетраэдр в точку начала координат, то можно составить уравнения равновесия для компонент силы, действующей на наклонную площадку:

(1.30)

Рис. 1.1. Элементарный тетраэдр

Обозначив площадь наклонной площадки через S, уравнения равновесия можно записать так:

(1.31)

где n₁, n₂, n₃ – проекции нормального единичного вектора на оси координат.

Вектор силы можно представить в виде суммы компонент:

(1.32)

где _i – единичные вектора вдоль ортогональных осей координат.

Подставив в уравнение (1.32) выражения компонент вектора силы из уравнений равновесия, получим

. (1.33)

Заметим, что для симметричного тензора  произведение на единичный нормальный вектор к наклонной площадке имеет вид

. (1.34)

Значит, сила, приходящаяся на единицу площади, может быть выражена следующим образом:

. (1.35)

В пределе стягивания тетраэдра в точку величина представляет собой силу, приходящуюся на единицу наклонной площадки, ориентацию которой характеризует нормальный единичный вектор . Величина  называется тензором напряжения в данной точке и записывается в матричной форме:

. (1.36)

Для доказательства симметричности этого тензора выделим из среды плоскостями, параллельными координатным плоскостям, прямоугольный параллелепипед (рис.1.2), вращение которого могут обусловить тангенциальные силы F₁, F₂, F₃, F₄.

Рис. 1.2. Выделенный из среды параллелепипед

Силы на гранях параллелепипеда можно выразить через диагональные компоненты тензора напряжений и размеры тела. Например:

; (1.37)

. (1.38)

Затем вычисляются моменты этих сил относительно оси, проходящей через точку центра масс параллелепипеда и параллельной оси x₃:

. (1.39)

Тогда

(1.40)

Теперь можно записать уравнение вращательного движения параллелепипеда:

(1.41)

где момент инерции параллелепипеда относительно оси вращения, проходящей через центр масс, определяется выражением

(1.42)

Тогда уравнение движения приобретает вид

(1.43)

и очевидно, что

(1.44)

Аналогично, рассматривая вращение вокруг двух остальных ортогональных осей, можно доказать равенство других диагональных элементов тензора напряжений:

. (1.45)

Следовательно, тензор напряжений в точке среды симметричный.