3.9. Сопротивление движению лопасти смесительного аппарата

Рассмотрим задачу (рис. 3.5), полагая наклон верхней пластины (лопасть мешалки) незначительным и задавая в случае обращенного движения скорость перемещения нижней горизонтальной пластины в отрицательном направлении оси x.

Рис. 3.5. Схема обращенного движения лопасти

В общем виде проекция уравнения движения на ось х имеет вид

, (3.121)

где  – плотность; t – время; v_х, v_у, v_z – проекции скорости частицы жидкости на оси х, у, z; р – давление; _хх, _ух, _zх – касательные напряжения на площадках, перпендикулярных первому индексу в направлении второго индекса; q_x – проекция ускорения свободного падения на ось х.

В силу горизонтальности оси х q_x = 0. Пусть поток стационарный, тогда ; из-за малого наклона верхней пластины и ламинарности потока . Полагаем, что компоненты скорости по осям у и z отсутствуют (v_z = v_у = 0). Полагаем также, что напряжения сдвига не меняются в направлениях x и z . Тогда напряжение сдвига _ух будет функцией координаты y и, опуская индексы при напряжениях, получим из (3.121) уравнение движения равновесия вида

(3.122)

или, приняв

(у) = ₁(у) + ₂(у), (3.123)

. (3.124)

Физически это означает разбиение задачи на две: течение между неподвижными пластинами под действием перепада давлений внутри участка а и течение под действием движения нижней пластины при отсутствии перепада давлений.

Пусть жидкость подчиняется степенному закону

(3.125)

где  – коэффициент динамической вязкости;  – скорость сдвига, здесь ; ₀, – напряжение сдвига и скорость сдвига при произвольно выбранном приведенном состоянии течения (обычно принимают = 1 с^–1); ₀ – коэффициент динамической вязкости при скорости сдвига ; n – реологическая константа жидкости (индекс течения).

Часто реологический степенной закон представляют в виде

, (3.126)

где k – реологическая константа жидкости, коэффициент консистенции.

Сравнение формул (3.125) и (3.126) дает

. (3.127)

Интегрируя уравнение (3.124) для ₁, получим

. ( 3.128)

В силу симметрии потока при у = 0 ₁ = 0 и С₁ = 0.

Реологическое уравнение можно записать в виде

. (3.129)

Приняв = 1 и используя закон (3.125), получим

. (3.130)

Тогда из выражений (3.128) и (3.130) получим

(3.131)

и

. (3.132)

По условию прилипаемости жидкости к неподвижным стенкам канала запишем

. (3.133)

Определив по условиям (3.133) константу интегрирования С₂, запишем

(3.134)

или, в силу равенства ,

. (3.135)

Проведем преобразование и интегрирование для потока под действием движения нижней пластины:

(3.136)

.

Запишем краевые условия и определим константы интегрирования С₄ и С₅:

;

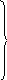
(3.137)

;

Тогда при

. (3.138)

По принципу аддитивности решений получим

. (3.139)

Продолжим решение в линейной постановке, аналогичной задаче Рейнольдса–Релея.

При n = 1 получим из выражения (3.139)

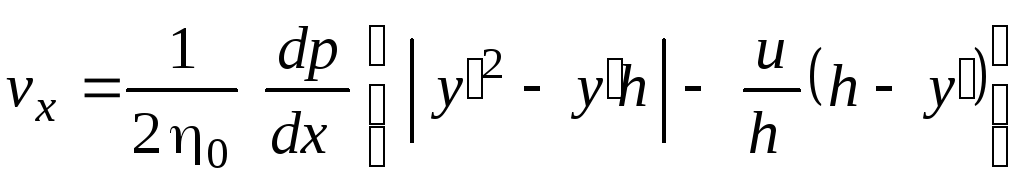. (3.140)

Полагая расход через любое поперечное сечение щели постоянным, запишем

. (3.141)

Подставив скорость v_x по формуле (3.140) в (3.141) и проведя интегрирование, получим

. (3.142)

На участке х = 0а в некоторой точке х_m выполняется условие . Пусть значению х_m соответствует ширина щели h_m, тогда из выражения (3.142) следует C₆ = Uh_m и можно записать зависимость (3.142) в виде

. (3.143)

Из геометрических соображений (см. рис. 3.5) свяжем переменные х и h:

. (3.144)

Тогда левую часть уравнения (3.143) можно преобразовать так:

. (3.145)

Подставив выражения (3.145) в (3.143) и разделив переменные, получим

; (3.146)

. (3.147)

Полагая, что давление вне зазора равно р₀, запишем условия

р = р₀ при h  h₀ и h  h₁ = h₀ (1 + k). (3.148)

Условия (3.148) и выражение (3.147) дают систему уравнений для нахождения констант h_m и С₇:

;

(3.149)

.

Решая систему (3.149) и опуская выкладки, получим

(3.150)

и

. (3.151)

Подставляя значения констант h_m и C₇ по формулам (3.150) и (3.151) в формулу (3.147), получим

. (3.152)

В силу уравнения (3.144) между переменными h и x получим

(3.153)

и из формулы (3.152) получим распределение давления потока на пластину:

. (3.154)

Теперь можно рассмотреть подъемную силу R, действующую на пластину:

. (3.155)

В результате интегрирования

. (3.156)

Эта нелинейная функция от переменной K имеет максимум. Для отыскания величины K для R_max проведем дифференцирование выражения (3.156) по K и приравняем производную к нулю:

= 0. (3.157)

Решение уравнения (3.157) дает значение K ≈ 1,188. Анализ функции (3.155) и уравнения (3.156) удобно производить при помощи программы MathCаd, расчеты и графики по которой приведены ниже.

Запишем функцию подъемной силы R с точностью до постоянного множителя, где K = x:

. (3.158)

Программа MathCad позволяет получить график функции f(х) – рис. 3.6. Очевидно, график имеет экстремум в области х = 1. Для уточнения аргумента х возьмем производную из выражения (3.158):

(3.159)

и решим задачу, приравняв эту производную к нулю:

; (3.160)

f₂ (x) = 0. (3.161)

Решение системы (3.160), (3.161) можно представить графически (рис. 3.7).

И

Рис. 3.6. График функции по уравнению (3.158)

Рис. 3.7. Графическое решение поиска точки приложения максимальной подъемной силы

з cказанного следует, что R_max имеет место при k ≈ 1,188 или при соотношении . Тогда максимальная подъемная сила выражается формулой вида

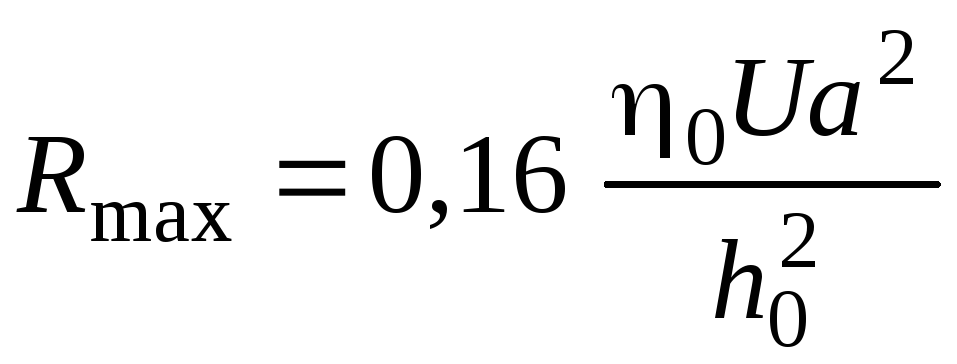. (3.162)

Ввиду малости наклона верхней пластины примем касательные напряжения на нижней пластине удовлетворяющими выражению

. (3.163)

Взяв производную по у′ из выражения (3.140), получим

. (3.164)

Подставим выражение (3.164) в правую часть формулы (3.163):

. (3.165)

Используя формулы (3.143), (3.144) и (3.150), подставим в правую часть формулы (3.165) выражения для , h и h_m; после несложных алгебраических выкладок получим формулу вида

. (3.166)

Силу сопротивления получим в результате интегрирования выражения (3.166):

; (3.167)

. (3.168)

Формулы (3.162) и (3.168) позволяют рассчитать максимальную подъемную силу и силу сопротивления при значениях, например,

а = 0,2 м; h₀ = 10^–4 м; U = 0,3 м/с; ₀ = 10^–1 Па · с.

С помощью программы MathCad получены величины

F_max = 45,256 H; R_max = 1,9210⁴ H. (3.169)

Для прочностного расчета крепления лопасти мешалки вычислим точку приложения равнодействующей силы сопротивления движению. Составим выражения для момента равнодействующей М_С:

(3.170)

;

. (3.171)

При k = 1,2 x_R  0,42 а.