2.5. Теория конических пластометров

П

Рис. 2.4. Расчетная схема конического пластометра Ребиндера

ринцип действия конического пластометра Ребиндера ясен из расчетной схемы (рис. 2.4). Конический индентор внедряется в испытываемую среду силой Р и достигает равновесия под действием этой силы и сил внутреннего сопротивления среды. Измеряется глубина внедрения конуса и по известным вертикальной силе и угле при вершине конуса рассчиты­ваются реологические показатели свойств среды, приборов для изме­рения твердости в материаловедении. Известно, что при попытках связать показатели твердости металлов с предельным напряжением текучести или временной прочно­сти возникают определенные труд­ности и появляется необходимость использования эмпирических данных. Можно ожидать, что в теории конических пластометров возникают такие же проблемы.

Действительно, Ребиндер и Ямпольский назвали расчетный реологический параметр среды пластической прочностью и предложили для ее расчета две формулы:

; (2.137)

. (2.138)

Однако оба расчетных параметра не являются предельным напряжением сдвига среды. В частности, по формуле (2.137) получаемый параметр в 1,5–2,5 раза больше, чем действительное предельное напряжение сдвига среды, которое можно определить на реометрах других конструкций.

Если полагать, что расчетная величина независима от угла конуса и соотношения силы и квадрата глубины пенетрации, то она инвариантна к параметрам прибора и условиям опыта. Формулы Ребиндера удобны и в том смысле, что они линейны к силе и расчетный параметр можно определить на основании одного опыта. В практике измерений обычно ступенчато наращивают вертикальную силу, измеряют прирост глубины пенетрации и получают более точно величину расчетного параметра – пластической прочности.

Если параметр пластической прочности предполагают использовать для контроля технологических процессов и связывают его с такими показателями, как, например, температура, состав среды, или другими показателями технологического процесса, то не возникнет никакой проблемы, поскольку будет использоваться относительная величина механически не совсем ясного реологического параметра – пластической прочности. Однако в целях использования опытной величины для реодинамического моделирования процессов течения или формосохранения нужен объективный безотносительный показатель – предельное напряжение сдвига.

Задачу получения на коническом пластометре предельного напряжения сдвига среды решали Агранат, Воларович и Широков, используя для этого задачу теории пластичности о проникновении конуса в пластичную полуплоскость. В результате они аналитически получили коэффициент, зависящий от угла при вершине конуса, вида

. (2.139)

Тогда формула Ребиндера с коэффициентом конуса Аграната–Воларовича–Широкова действительно стала давать хорошие результаты при угле при вершине конуса около 60, совпадающие с предельным напряжением сдвига, измеренным на пластометрах других конструкций. Коэффициент Ямпольского–Ребиндера при угле 60 равняется 0,413; коэффициент Аграната–Воларовича–Широкова составляет 0,214. Теперь с помощью пластометра Ребиндера можно найти предельное напряжение сдвига (Н/м²) материала изделий по формуле

, (2.140)

где k – коэффициент прибора, функция угла при вершине конуса; P – вертикальная сила, вдавливающая конус в материал, Н; h – глубина проникновения конуса в материал, м.

Однако расчеты, произведенные с использованием методов теории распознавания образов, показали, что в этом случае предельное напряжение сдвига оказывается функцией угла при вершине конуса, что особенно заметно при малых углах. Объясняется это тем, что при выводе корректирующего коэффициента было использовано решение задачи теории пластичности с учетом только нормальных напряжений на поверхности конуса, а поскольку уравнение (2.140) по существу является уравнением равновесия конуса в проекциях на вертикальную ось, то при углах при вершине конуса более 60 касательные напряжения, имеющие место на поверхности конуса, не вносят существенного вклада в уравнение равновесия. Расчеты показали, что если коэффициент Ямпольского–Ребиндера при угле конуса 10 равен 3,61, то коэффициент Аграната–Воларовича–Широкова составляет 7,25, что значительно искажает результаты измерений предельного напряжения сдвига, которые в этом случае нельзя использовать при реодинамическом математическом моделировании процессов переработки пищевых продуктов.

Разумеется, для контроля качества и управления технологическими процессами, когда абсолютные значения предельного напряжения сдвига не так важны, можно пользоваться любой из приведенных констант прибора. Следует отметить, что если исследуемый материал не прилипает к поверхности конуса и касательными напряжениями можно пренебречь, то вывод Аграната–Воларовича–Широкова теоретически обоснован. Однако большинство мясомолочных продуктов проявляют существенные адгезионные свойства при взаимодействии с металлом конуса прибора.

Зависимость коэффициента Аграната–Воларовича–Широкова от угла при вершине конуса вынудила искать решение, учитывающее наличие касательных напряжений на поверхности конуса и позволяющее использовать данные конического пластометра при малых углах конуса пенетрометра.

Запишем условие равновесия конуса в проекциях на вертикальную ось:

, (2.141)

где ,  – нормальное и касательное напряжения на поверхности конуса в предположении, что они распределены равномерно; S_k – площадь внедренной части конуса.

Из геометрии получим, что

. (2.142)

Полагаем

, (2.143)

где E, G – модули упругости первого и второго рода; ,   – деформации растяжения–сжатия и сдвига;  – коэффициент Пуассона.

С помощью выражений (2.143) преобразуем выражение (2.141) к виду

. (2.144)

По гипотезе максимальных касательных напряжений теории пластичности запишем

. (2.145)

С учетом (2.144) выразим из (2.145) максимальные нормальные напряжения:

. (2.146)

Запишем условие эквивалентности проекций нормальных сил на вертикальную ось при равномерном распределении нормальных напряжений и при действительном распределении, что было определено в решении Аграната–Воларовича–Широкова без учета касательных напряжений:

(2.147)

или

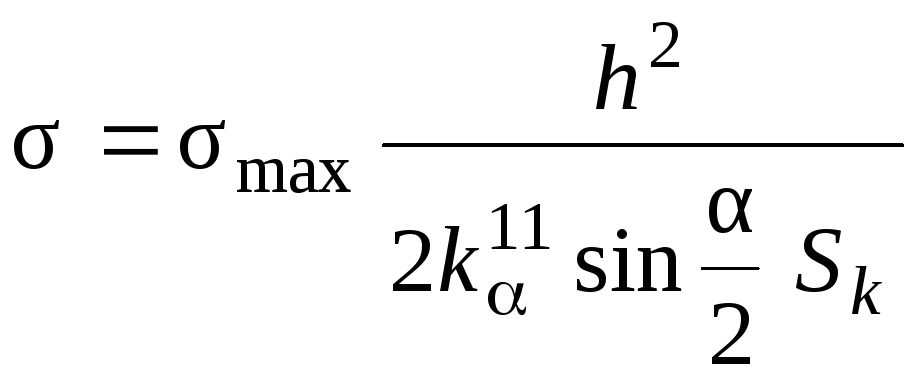. (2.148)

С учетом формулы (2.148) перепишем формулу (2.144) в виде

(2.149)

или

. (2.150)

Значения всех коэффициентов приведены в табл. 2.2.

Таблица 2.2