3.2. Графіки

Визначення. Множина Р називається графіком, якщо кожен його елемент є двійкою елементів деякої множини М.

Р=р|р=а, b> і а, bМ

Приклад. Р=а, b, 1, c, 2, 3

Якщо М - довільна множина, то М² - графік, будь-яка підмножина множини М² також є графіком.

Визначення. Множина проекцій графіка Р на першу вісь називається областю визначення графіка Р, множина проекцій графіка Р на другу вісь називається областю значень графіка.

Якщо відкласти по осі Х область визначення, а по осі Y область значень, то сам графік розміститься деякім чином на площині (рис. 3.1.).

Якщо графік Р=, то очевидно ін₁Р= і ін₂Р=.

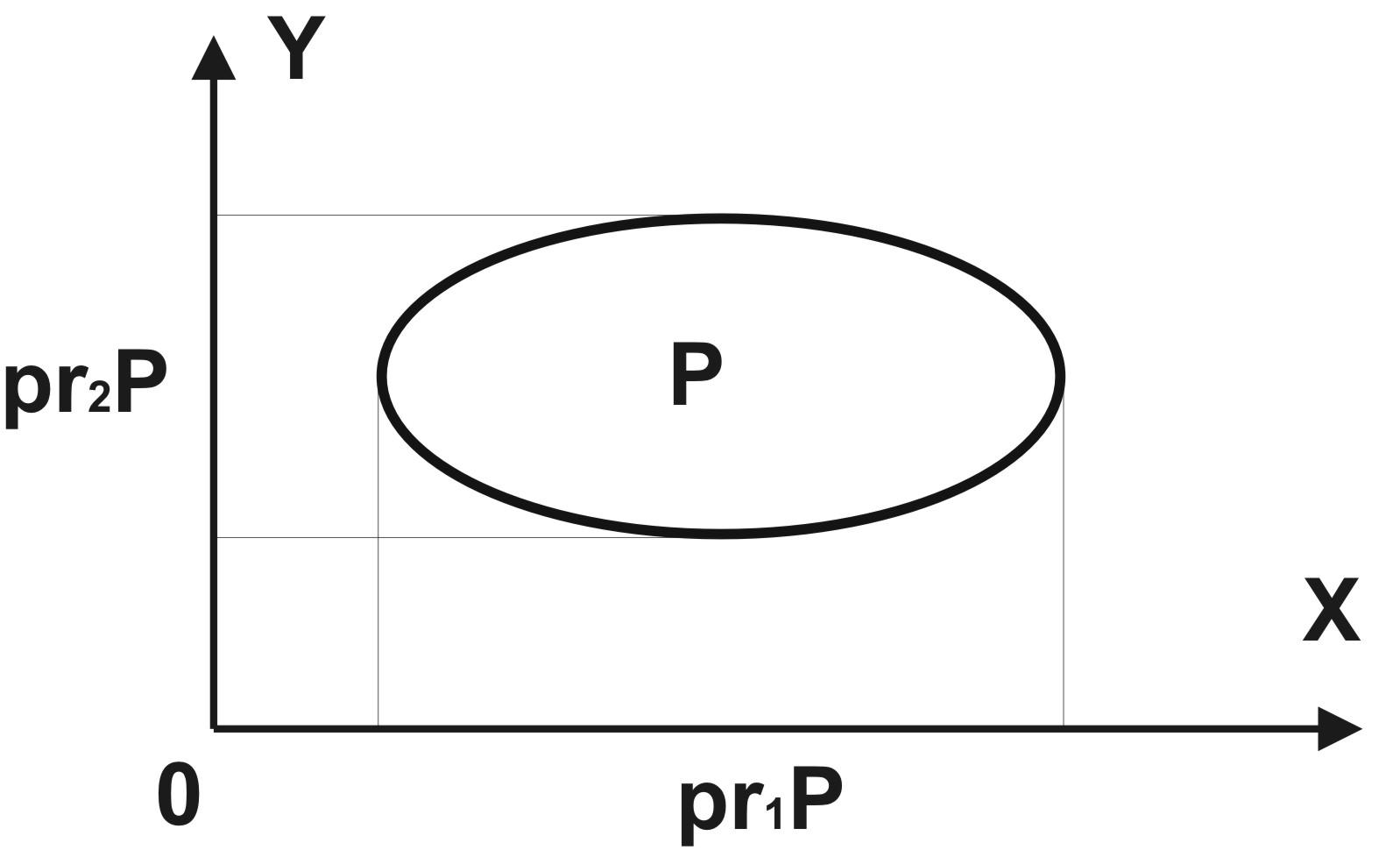
Рис. 3.1. Графік і його проекції на площині

Якщо графік по визначенню є множиною, то над графіками можуть виконуватися операції, що звичайна для множин, тобто   \,  .

Визначення. Двійка с, d називається інверсією двійки a, b, якщо компоненти с дорівнює b, та d дорівнює a.

Інверсія пари р=а, b позначається як р^-1.

Подвійна інверсія двійки (р^-1)^-1 дорівнює самій двійці (р^-1)^-1=р.

Визначення. Інверсією графіка Р, що позначається як Р^-1, називається множина інверсій усіх пар з Р

Р^-1=qР^-1|q=p^-1 і р

Приклад. Р=, а, b, P^-1=2, 1, b, a

При інверсії графіка Р пр₁^-1=пр₂Р і пр₂^-1=пр₁Р.

Визначення. Графік Р називається симетричним, якщо він поряд з кожною парою містить її інверсію

р  р^-1Р

Приклад. р=a, b, b, a, c, c

Для будь-якої множини М множина М² - симетричний графік, для будь-якого графіка Р Р^-1 і ^-1 - симетричні графіки.

Визначення. Графік R=PQ називається композицією графіків Р і Q, якщо двійка х, у належить R тоді і тільки тоді, коли існує такий елемент z, що двійка х, z належить Р и двійка z, у належить Q:

R=PQ=х, уR| існує z такий, що х, z і z, уQ

Приклад. Р=а, a, a, c, a, b, b, b, c, b

Q=a, b, a, c, c, з

R=P_ Q=a, b, a, c

Композиція графіків Р и Q порожня тоді, коли пр₂P₁пр₁P₂ = .

Визначення. Декартовим добутком Р₁ і Р₂ називається графік

Р₁Р₂=a₁, a₂, b₁, b₂|а_і, b_і_і , і=1,2

Визначення. Графік Р називається функціональним, якщо в ньому немає пар з однаковими першими і різними другими компонентами; графік Р називається ін’єктивним, якщо в ньому немає пара з однаковими другими і різними першими компонентами.

Приклад. ₁=a, b, a, з нефункціональний

₂=a, c, b, c неін’єктивний

Графік М² на довільній множині М не є функціональним і ін’єктивним, композиція функціональних графіків функціональна, композиція ін’єктивних графіків ін’єктивна, інверсія переводить функціональний графік у ін’єктивний, а ін’єктивний - у функціональний.

Операції над графіками мають спеціальні властивості:

1. Р₁_₂_ не комутативність

2. _(_____ асоціативність

3.  властивості границь

4. (Р__^-1_^-1_^-1

Контрольні запитання

1. Що таке упорядкована множина та як вона позначається?

2. Яка різниця між декартовим добутком і ступенем?

3. Які проекції можуть бути?

4. Які властивості мають операції над упорядкованими множинами?

5. Що є графіком?

6. Які операції можливі над графіками?

7. Які властивості мають графіки та операції над графіками?