8.3. Толерантність

Визначення. Відношення  на множині А називається відношенням толерантності, якщо воно рефлексивно і симетрично.

Синонімом толерантності є сумісність. Для відношення толерантності на відміну від відношення еквівалентності транзитивність не обов'язкова, отже, відношення еквівалентності - окремий випадок відношення толерантності.

Визначення. Класом сумісності називається підмножина А така, що будь-які два елементи а₁ і а₂, їй належні, є толерантними.

Клас сумісності називається максимальним, якщо він не є підмножиною ніякого іншого класу сумісності. Різні класи можуть містити однакові елементи, отже, є множинами, що Перерізають.

Теорема. Усяке відношення толерантності  на множині А задає покриття множини А, блоки покриття при цьому є і класами сумісності і, навпаки, усяке покриття множини А підмножинами з ₁, А₂,..., А_n визначає між елементами кожного з підмножин покриття деяке відношення толерантності.

Покриття множини може бути не єдиним, у зв'язку з чим важливе значення має пошук покрить з мінімальним, з урахуванням повторень, числом елементів у ньому, називаний задачею визначення мінімального покриття. Очевидно, що у випадку відношення еквівалентності абсолютно мінімальним покриттям є розбивка - мінімальне сумарне число елементів у ньому дорівнює потужності множини .

Приклад. А=пол, лицо, кит, море, мина. Пари слів належать відношенню , якщо вони мають загальну букву.

а) Таблиця 8.3.

	1	2	3	4	5
1	1	1		1
2	1	1	1	1	1
3		1	1		1
4	1	1		1	1
5		1	1	1	1

б)

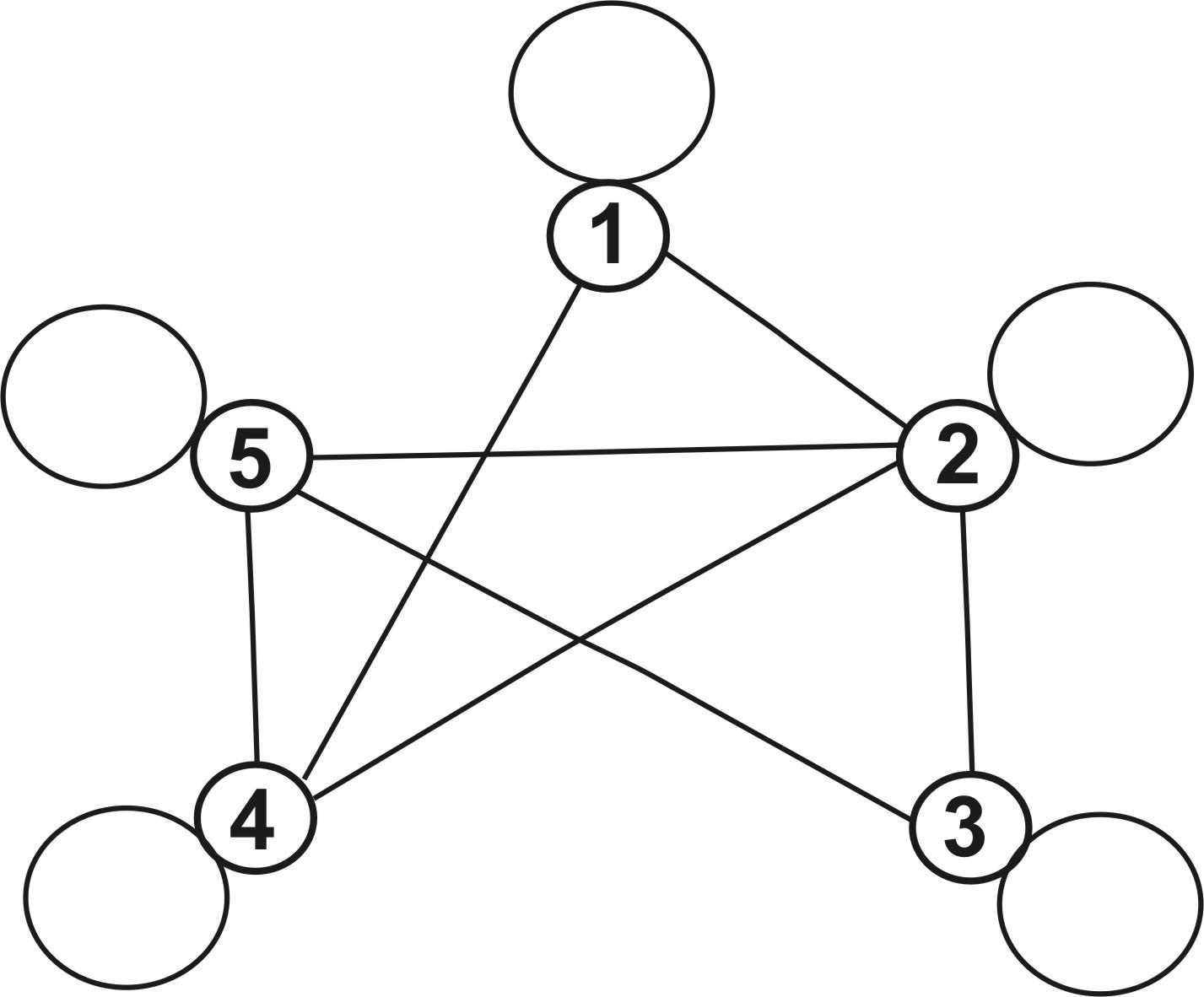
Рис. 8.3. Відношення толерантності:

в) {1, 2, 4}, {2, 3, 5}, {2, 4, 5} - максимальні класи сумісності, 1, 2, 2, 4, 2, 5, 3, 5, 4, 5 - не максимальні.

Покриття 1, 2, 4, 2, 3, 5, 2, 4, 5 взаємно однозначно відповідає відношенню толерантності =(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 2), (2, 1), (1, 4), (4, 1), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (3, 5), (5, 3), (4, 5), (5, 4).

8.4. Квазіпорядок

Визначення. Відношення  на множини А називається відношенням квазіпорядку, якщо воно рефлексивно і транзитивне.

Синонімом квазипорядку є передпорядок і передупорядкування.

Для відношення квазіпорядку на відміну від відношень еквівалентності і часткового порядку властивості відповідно симетричності й антисиметричності не обов'язкові, отже, відношення еквівалентності і часткового порядку - окремі випадки відношення квазіпорядку.

Приклад. Відношення подільності на множини цілих чисел (позитивних, негативних і нуля) є відношенням квазіпорядку

а) Таблиця 8.4.

	-1	0	1	2	3	4
-1	1	1	1	1	1	1
0		1
1	1	1	1	1	1	1
2		1		1		1
3		1			1
4		1				1

б)

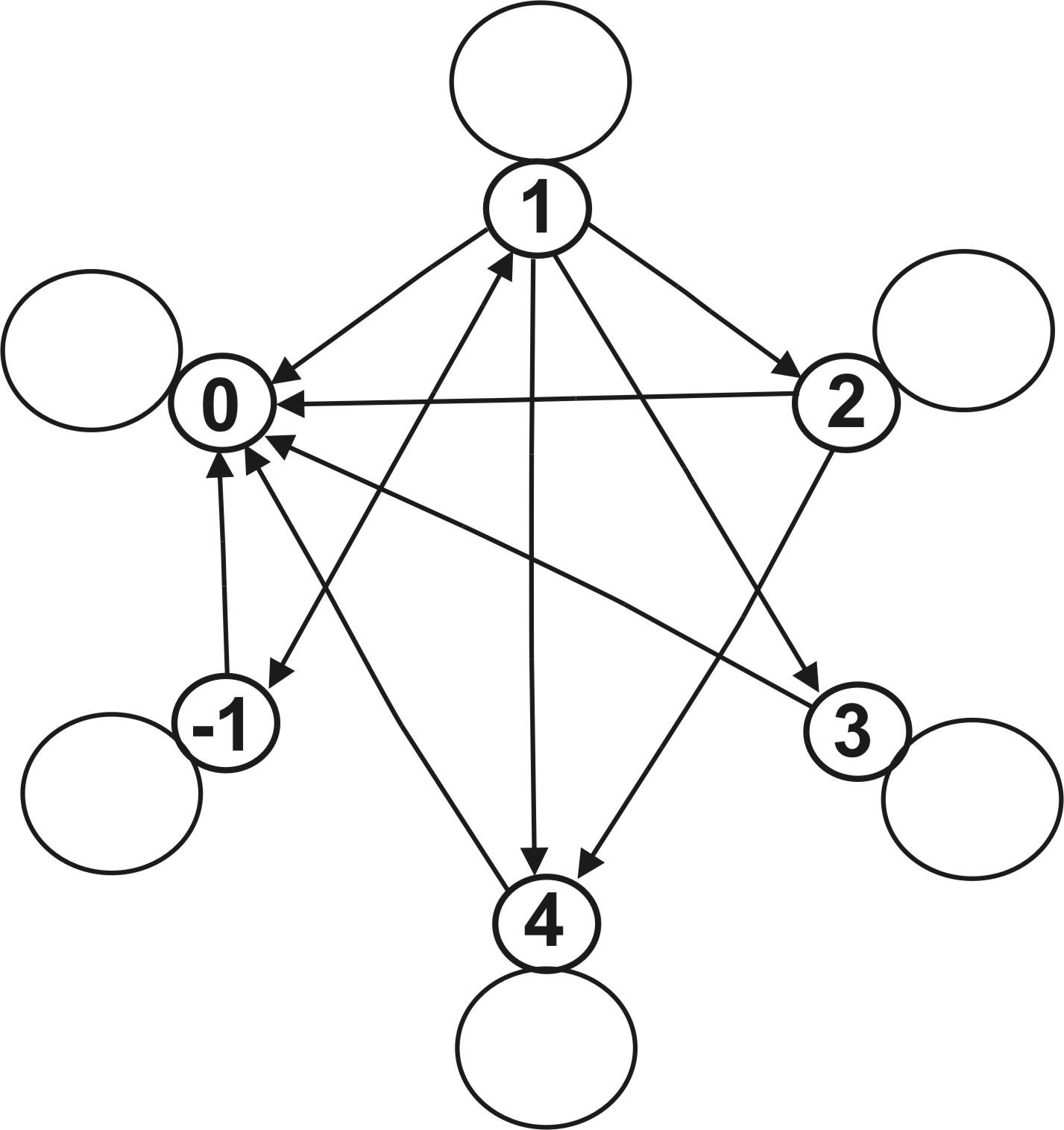
Рис. 8.4. Відношення квазіпорядку

Контрольні запитання

1. Які властивості має відношення еквівалентності?

2. Якій зв’язок між розбивками і відношенням еквівалентності?

3. Що є фактор-множиною А_А, і суміжним класом елемента а по відношенню _А?

4. Що є природним відображенням множини А на фактор-множину А і системою представників відповідного відношення еквівалентності?

5. Яка різниця між суворим і несуворим порядком?

6. Чи усі елементи можна порівняти? Що є ланцюгом?

7. Що є розбивкою А? Що є підрозбивкою розбивки А?

8. Що є передуванням векторів і лексіграфічним порядком?

9. Що є толерантністю, або сумісністю, у чому різниця між класами суміжності і сумісності?

10. Що є покриттям, мінімальним покриттям?

11. Які властивості має квазіпорядок?

12. Для яких відношень квазіпорядок є узагальненням?