Список літератури Основна

1. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.: Учебно-методический кабинет высшего образования, 1992. - С.137-148.

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.94-98.

3. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.55-73.

Додаткова

4. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979. - С.23-35.

5. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.504-522.

Для практичних занять

6. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.30-35.

7. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1973. - С.50-77.

Лекція 26. Графічна та таблична мінімізація

Вступ

Лекція має за мету навести два найбільш наочних метода мінімізації булевих функцій. Розглянута відповідність між мінтермами (макстермами) та елементами n-вимірного куба, а також мінтермами та клітками таблиці Карно і Закревського. Звернено увагу до кодування стовпців та рядків карт Карно і Венна, до обмежень графічного і табличного методів.

У лекції присутні два підрозділи:

1. Графічний метод мінімізації булевих функцій

2. Табличний метод мінімізації

26.1. Графічний метод мінімізації булевих функцій

Кожній вершині n-мірного куба можна поставити у відповідність константу одиниці. Отже, підмножина відзначених вершин є відображенням булевої функції від n змінних у СДНФ.

Для відображення функції від n змінних, представленої в СДНФ, необхідно установити відповідність між її мінтермами й елементами n-вимірного куба.

Мінтерм n-го рангу для функції n-змінних відповідає вершині n-вимірного куба. Мінтерм (n-1)-го рангу можна розглядати як результат доповнення двох мінтермів n-го рангу, що відрізняються однією змінною:

_n-1=(_n-1x_i)(_n-1x_i).

На n-вимірному кубі це відповідає заміні двох вершин, що відрізняються значенням одної змінної, ребром, що з'єднує ці вершини. Говорять, що ребро покриває інцидентні йому вершини. Таким чином, мінтермам (n-1)-го порядку відповідають ребра n-вимірного куба.

Аналогічно установлюється відповідність мінтермів (n-2)-го порядку граням n-вимірного куба, кожна з яких покриває чотири вершини або два ребра (квадрат).

Елементи n-вимірного куба, що характеризуються S вимірами, називаються s-кубами. Так вершини називаються 0-кубами, ребра - 1-кубами, грані - 2-кубами і т.д. Таким чином, будь-яка ДНФ відображається на n-вимірному кубі сукупністю S-кубів, що покривають усі відзначені вершини, які відповідають конституентам «1» (0-кубам). Говорять, що така сукупність S-кубів чи мінтермів утворить покриття функції.

Приклад. Для функції від трьох змінних y= x₁x₂x₃  x₁x₂ x₃  x₁x₂ x₃ x₁ x₂ x₃ x₁ x₂x₃  x₁ x₂ x₃, заданої у вигляді СДНФ, графічний метод дає формулу вигляду y_min= x₃x₁x₂  x₁x₂ = x₃  (x₁  x₂).

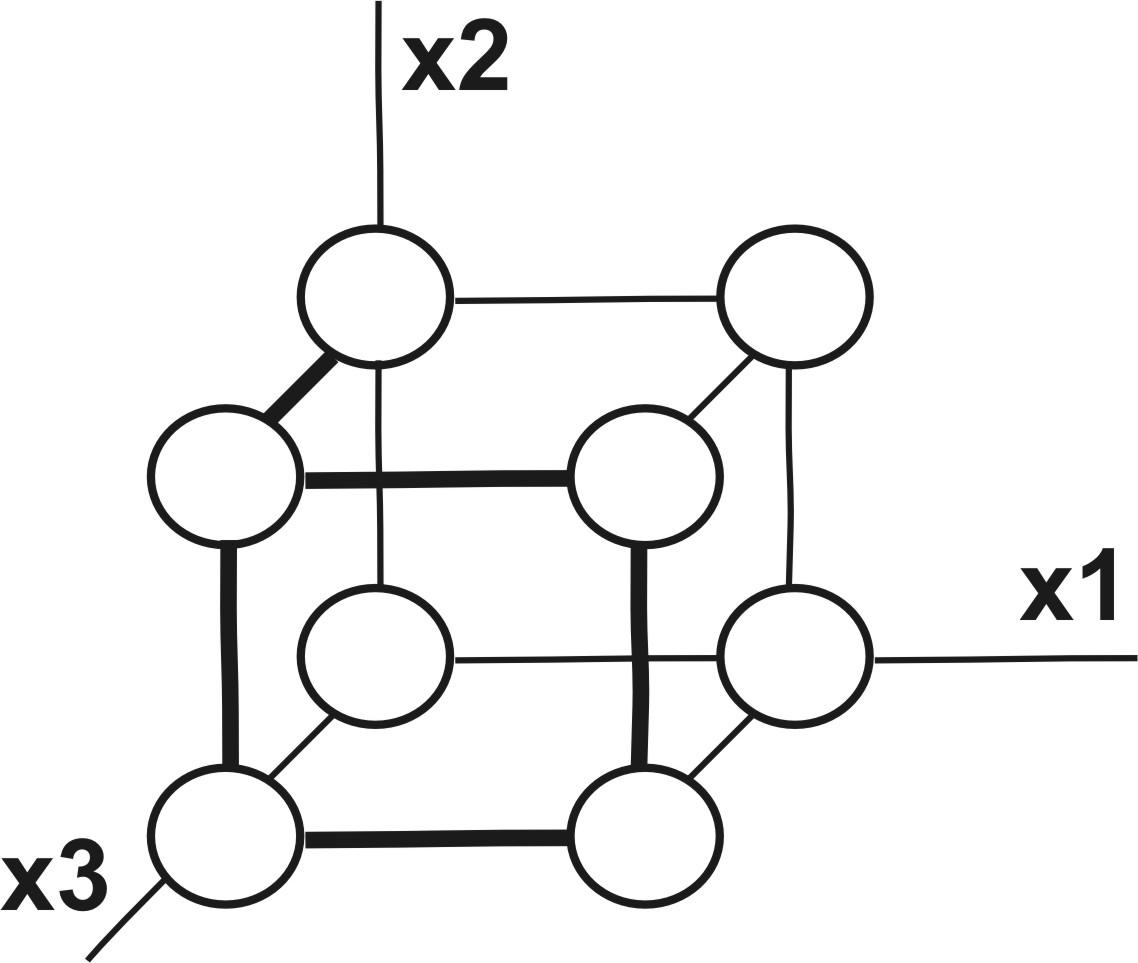
Рис. 26.1. Грань і ребра для функції y_min = x₃ x₁ x₂  x₁x₂ у графічному методі мінімізації

Мінімізація на n-вимірному кубі зводиться до пошуку такого покриття, число S-кубів якого буде мінімально, а їхня розмірність S максимальна. Таке покриття називають мінімальним покриттям, а відповідна йому ДНФ - мінімальною ДНФ (МДНФ).

Аналогічно можна виконати мінімізацію графічним способом для КНФ, для цього необхідно замість СДНФ і мінтермів розглядати СКНФ і макстерми.

Даний метод наочний і простий при n=3. При n4 метод складний.