Список літератури Основна

1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.35-38.

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - с.43-46.

3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. – К.:Наук. думка, 1989. - С.35-50.

4. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.97-115.

5. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. - С.62, 63.

Додаткова

6. Горбатов В.А. Основы дискретной математики. – М.: Высш. шк., 1986. - С.13-20.

7. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. - С.42-46.

Для практичних занять

8. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.15-17.

Лекція 8. Спеціальні види відношень

Вступ

Лекція має за мету навести поняття спеціальних бінарних відношень, що використовуються значно частіше за інші. Розглянуто еквівалентність, несуворий і суворий порядки, толерантність, квазіпорядок, а також множині властивостей спеціальних відношень. Звернено повагу на вигляд матричного, графового і множинного завдання спеціальних відношень.

У лекції присутні чотири підрозділи:

1. Еквівалентність

2. Порядок

3. Толерантність

4. Квазіпорядок

8.1. Еквівалентність

Визначення. Бінарне відношення _А на множини А, що задовольняє властивостям рефлективності, транзитивності і симетричності, називається відношенням еквівалентності (.

Очевидно, що якщо _А - відношення еквівалентності на множині А, то обернене відношення _А^-1 також є відношенням еквівалентності на даній множині.

Відношення еквівалентності на множині А зв'язано з розбивками цієї множини на попарно непересічні підмножини, що завдає належність кожного елементу множини А тільки одному класу розбивки.

Нехай _А - деяке відношення еквівалентності на множини А, що не порожня. Розглянемо фактор-множину А_А=Sа(_А)|а.

Визначення. Переріз S_a(_A) називається суміжним класом елемента а по відношенню _А.

Лема. Фактор-множина А_А по відношенню еквівалентності _А є розбивкою множини А на суміжні класи S_a(_A)=A.

Тому що _А – рефлексивно, справедливо аS_a_ для кожного с такого, що сS_a_S_b_, виконується а_Ас і b_c, у силу симетричності а_с і с_Аb, у силу транзитивності а_b і S_a(_A)S_b(_A), у силу симетричності b_Aa і S_b(_)S_a(_A), тобто S_a(_S_b(_A), таким чином різні суміжні класи не перерізаються.

Кожній розбивці R(A)={A₁, A₂,..., A_k} множини А відповідає відношення еквівалентності _ на множині А, суміжні класи якого збігаються з класами даної розбивки, тобто а_b тоді і тільки тоді, коли а,b_і, де і=1, 2,..., k.

Теорема. Кожному відношенню еквівалентності на множині А відповідає єдина розбивка R(A) даної множини і, навпаки, будь-якій розбивці множини А однозначно відповідає деяке відношення еквівалентності на А.

Зв'язок відношень еквівалентності і розбивок множин можна використовувати при визначенні поняття кардинального числа, якщо вважати, що дві множини еквівалентні тоді і тільки тоді, коли вони рівно потужні. У цьому випадку кожному класу еквівалентності відповідає визначена потужність (кардинальне число), причому деякому класу розбивки скінченних множин відповідає натуральне число - число елементів у множинах з даного класу.

Нехай  - відношення еквівалентності на множини А, A/=S_a()/a - фактор-множина множини А по даному відношенню еквівалентності.

Визначення. Відображення множини А на фактор-множину А, що зіставляє кожному елементу а суміжний клас S_a(), якому належить елемент а, називається природним відображенням множини А на фактор-множину А.

Нехай  - відображення множини А на множину В. Відображенню  відповідає деяке цілком визначене відношення еквівалентності  на множині А. Нехай для елементів а₁, а₂ а₁а₂ тоді і тільки тоді, коли (а₁)а₂). При зіставленні кожному елементу b його повного прообразу при відображенні  виходить взаємно однозначне відображення  множини В на фактор-множину А, причому композиція  збігається з природним відображенням множини А на фактор-множину А.

Всі елементи, що належать деякому класу А_і розбивки R={A₁,..., A_n} множини А, зв'язані відношенням еквівалентності і взаємозамінні у тому сенсі, що кожний з цих елементів визначає даний клас, тобто може служити його представником (еталоном).

Визначення. Підмножина множини А, що містить по одному і тільки одному елементу а_і з кожного класу А_і деякої розбивки Р={A₁, A₂, ... , A_i,..., A_n} множини А, називається системою представників відповідного відношення еквівалентності.

Приклад. а) Нехай є множини А = {а₁, а₂, а₃ і B = {b₁, b₂, b₃,b₄ b₅, b₆, b₇}. Р₁а₁, а₂, а₃, _А,1=а₁, a₁>, <a₁, a₂>, <a₁, a₃>, <a₂, a₁>, <a₂, a₂>, <a₂, a₃>,<a₃, a₁>,<a₃, a₂>, <a₃, a₃>}; P₂={{a₁}, {a₂}, {a₃}}, _A,2={<a₁, a₁>, <a₂, a₂>, <a₃, a₃>} P_B={{b₁, b₂, b₃}, {b₄}, {b₅, b₆, b₇}} _B={(b₁, b₁), (b₁, b₂), (b₂, b₁), (b₂, b₂), (b₁, b₃), (b₃, b₁), (b₃, b₃), (b₂, b₃), (b₃, b₂), (b₄, b₄), (b₅, b₅), (b₅, b₆), (b₆, b₅), (b₆, b₆), (b₅, b₇), (b₇, b₅), (b₇, b₇), (b₆, b₇), (b₇, b₆)}

б) Таблиця 8.1.

B	b1	b2	B3	b4	b5	B6	b7
b1	1	1	1
b2	1	1	1
b3	1	1	1
b4				1
b5					1	1	1
b6					1	1	1
b7					1	1	1

в)

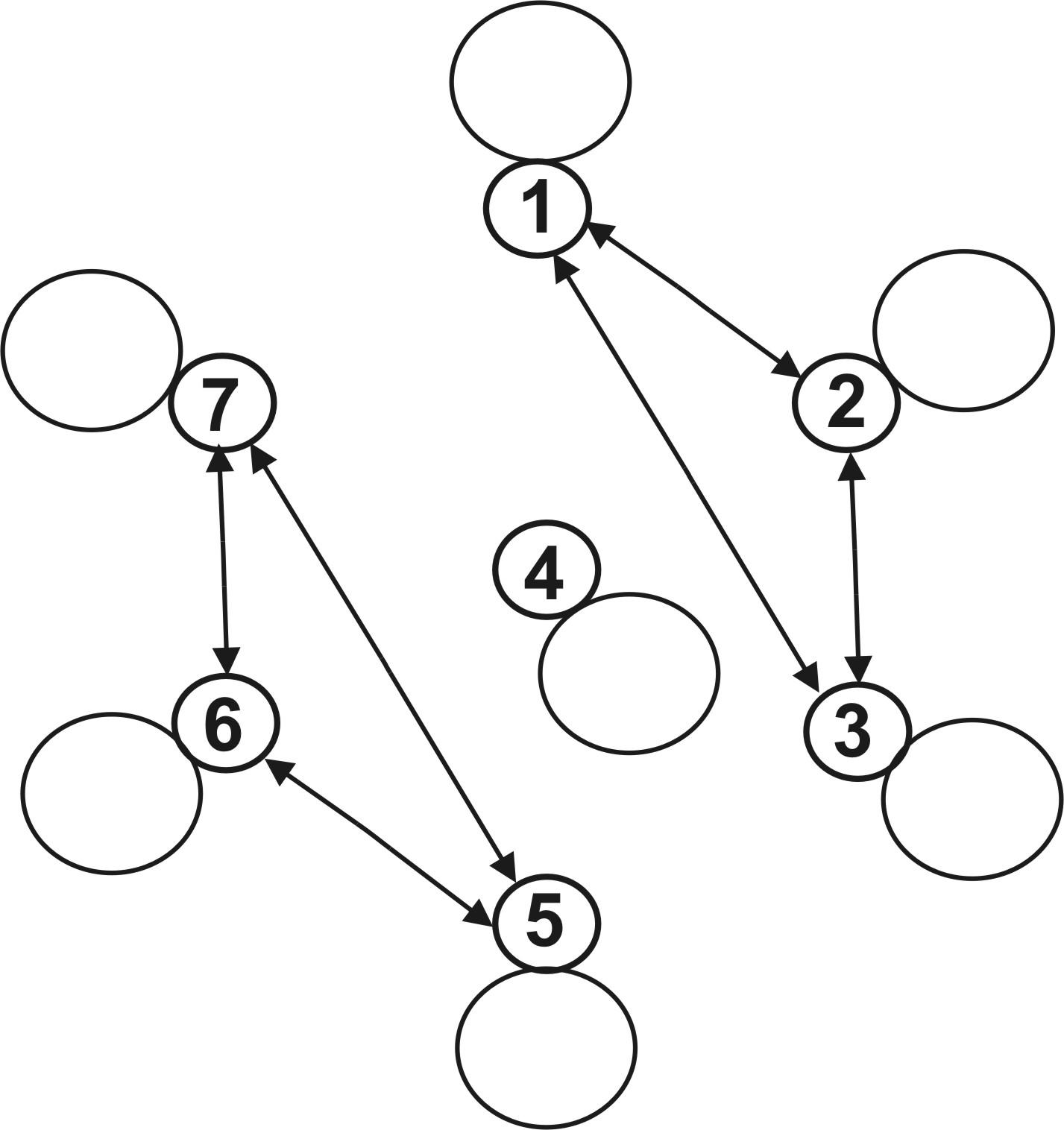
Рис. 8.1. Відношення еквівалентності _B