14.2. Способи представлення графів

Перший конструктивний спосіб, як відзначалося, - завдання графу G у вигляді двійки G=<X, Г>. За допомогою цього способу не можна задати мультиграф і псевдограф.

Більш складний аналітичний спосіб завдання відзначених графів у вигляді трійки G=<X, V, >, де  - відношення, що задається у свою чергу трійкою XVX, таке, що для <x_i, v_j, x_k> випливає, що дуга v_j V, з'єднує вершини x_i і x_k. Трійкою G=<X, V, > можна задати і мультиграф, і псевдограф.

Інший основний спосіб - завдання графу G за допомогою матриці. У матриці суміжності графу G рядка і стовпці відповідають вершинам графу, а елемент (клітка) матриці u_ij, що відповідає стовпцю x_i і x_j рядку, дорівнює числу кратних ребер, що зв'язують вершину x_i з вершиною x_j чи, для орграфу, числу дуг, спрямованих з вершини x_i у вершину x_j.

Приклад. Орієнтований граф, заданий матрицею суміжності і графічно

Т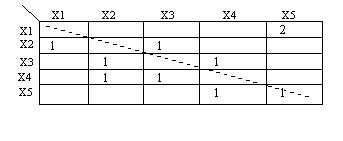аблиця 14.1

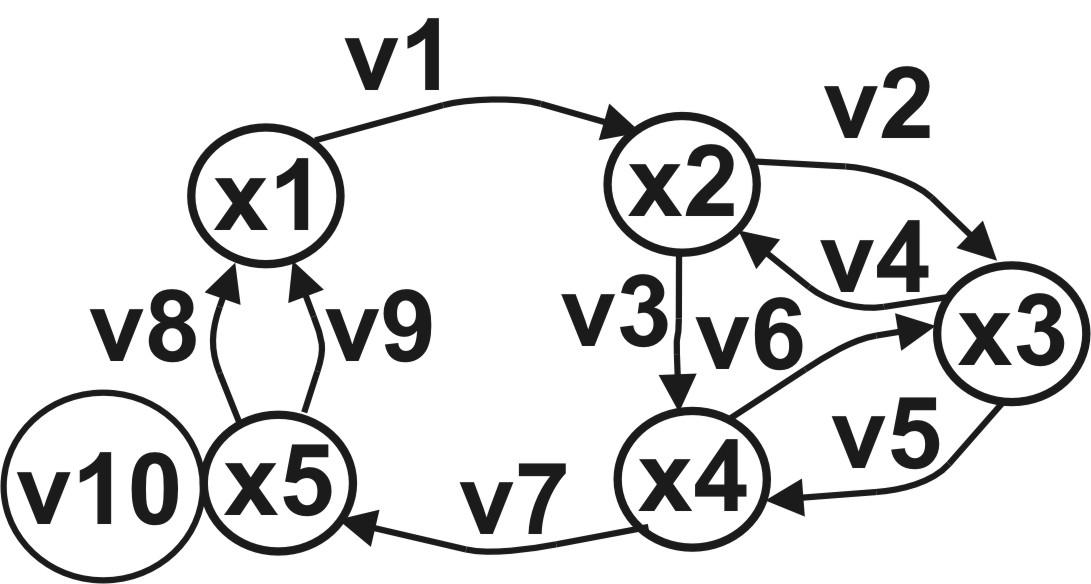
Рис.14.9. Орієнтований псевдограф G =<X, V>, X = {x1, x2, x3, x4, x5}, V = {v1, v2, v3, v4, v5, v6, v7, v8, v9, v10}

Очевидно, що для будь-якого орграфу на його матриці суміжності справедливо:

_{n n}

 x_i(s(x_i) = u_ij; p(x_i) = u_ji; G(x_i) = s(x_i) + p(x_i))

^{j=1 j=1}

Матриця суміжності орграфу в загальному випадку не симетрична.

Приклад. Неорієнтований граф, заданий матрицею суміжності і графічно

Таблиця 14.2

Рис. 14.10. Неорієнтований псевдограф : G =<X, V>, X = {x1, x2, x3, x4, x5}, V = {v1, v2, v3, v4, v5, v6}

Для неорієнтованого графу матриця суміжності симетрична.

Петля в матриці суміжності неорієнтованого графу вважається один раз, тоді для матриця суміжності будь-якого неорієнтованого графу справедливо:

_{n n}

 x_i(  v_j = <x_i, x_i>  G(x_i) =  u_ik і G(x_i) =  u_ik),

^{k=1 k=1}

_{n n}

 x_i (  v_j = <x_i, x_i>  G(x_i) = ( u_ik) + 1 і G(x_i) = 1+  u_ik).

^{k=1 k=1}

Якщо вершина є кінцем ребра, то говорять, що вершина інцидентна ребру, а ребро інцидентно вершині, чи вони інцидентні. Для орграфов розрізняють позитивну інцидентність, коли дуга виходить з вершини, і негативну інцидентність, коли дуга заходить у вершину.

Граф G можна задати матрицею інцидентності, стовпці якої відповідають ребрам (дугам) графу, а рядки - вершинам графу. Для неорієнтованого графу на перетинанні i-го рядка, що відповідає вершині x_i, і j-го стовпця, що відповідає ребру v_j, ставиться одиниця, якщо вершина x_i інцидентна ребру v_j. Для орграфу на перетинанні i-го рядка і j-го стовпця ставиться “+1”, якщо дуга v_j виходить з вершини x_i, і ставиться ”-1”, якщо дуга v_j заходить у вершину x_i. Кожен стовпець містить два елементи. Петлі зіставляють порожній стовпець, тоді матриця інцидентності задає графу без зазначення вершин, з якіми зв'язані петлі. Ця обстава вимагає спеціальних міток.

П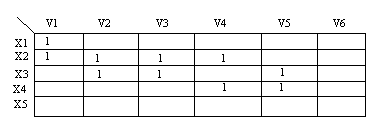риклад. Неорієнтований граф і його матриця інцидентності

Таблиця 14.3

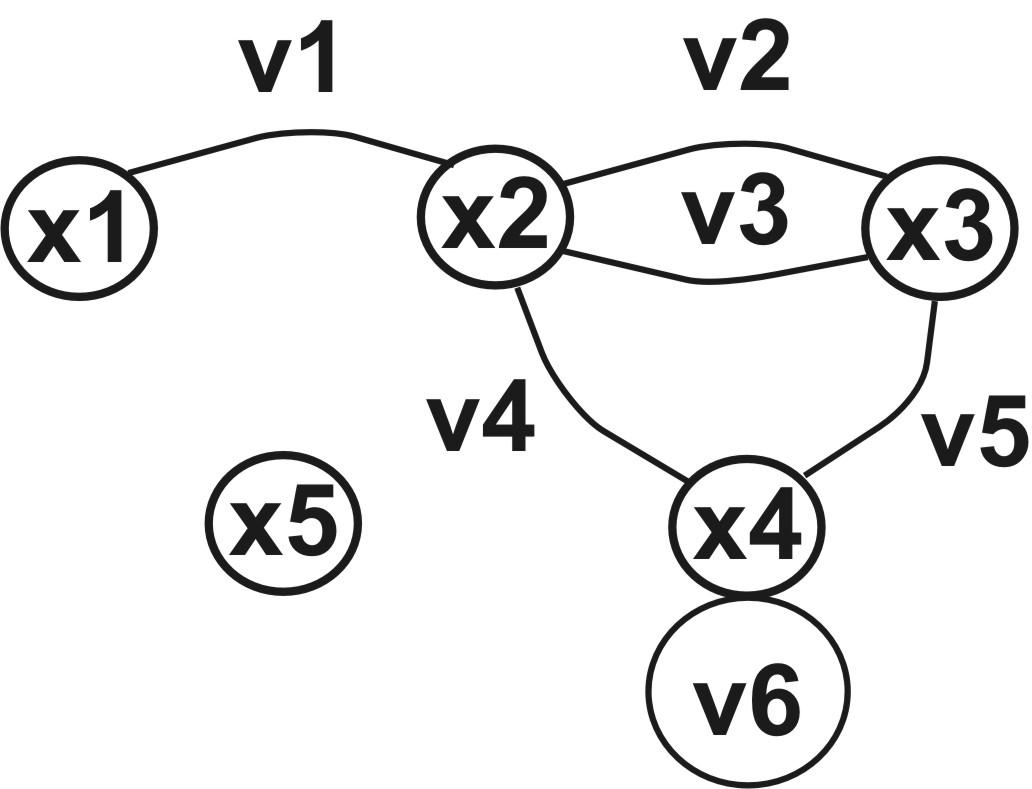
Рис. 14.11. Неорієнтований псевдограф G =<X, V>, X = {x1, x2, x3, x4, x5}, V = {v1, v2, v3, v4, v5, v6}

Для будь-якого неорієнтованого графу без петель і його матриці інцидентності справедливо:

_m

 x_i (G(x_i) =  u_ij), де m = V.

^j=1

Приклад. Орграф, заданий графічно і матрицею інцидентності

Т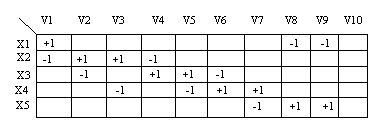аблиця 14.4

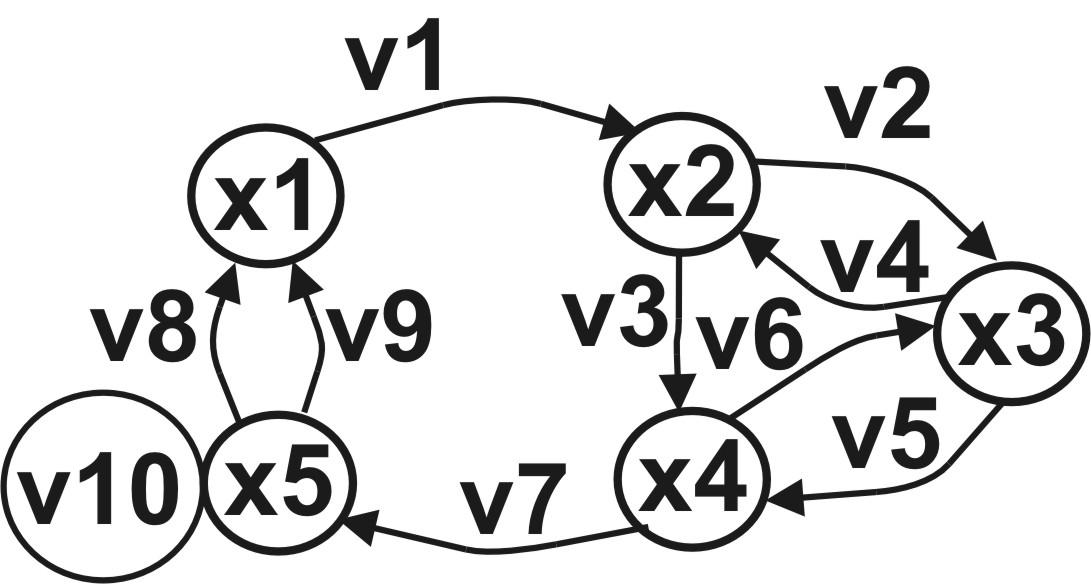
Рис. 14.12. Орієнтований псевдограф G =<X, V>, X = {x1, x2, x3, x4, x5}, V = {v1, v2, v3, v4, v5, v6, v7, v8, v9, v10}

Для будь-якого орієнтованого графу без петель і його матриці інцидентності справедливо:

_{m m m}

 x_i(s(x_i) =  u_ji ⁽⁺¹⁾; p(x_i) =  u_ji^(-1); G(x_i) = s(x_i) + p(x_i) =  u_ji ,

^{j=1 j=1 j=1}

де u_ji^(-1) {+1;0}, u_ji^(-1) {-1;0}.

Графи, для яких збігаються відношення інцидентності, називаються ізоморфними. Матриця інцидентності визначає графи без петель з точністю до ізоморфізму.

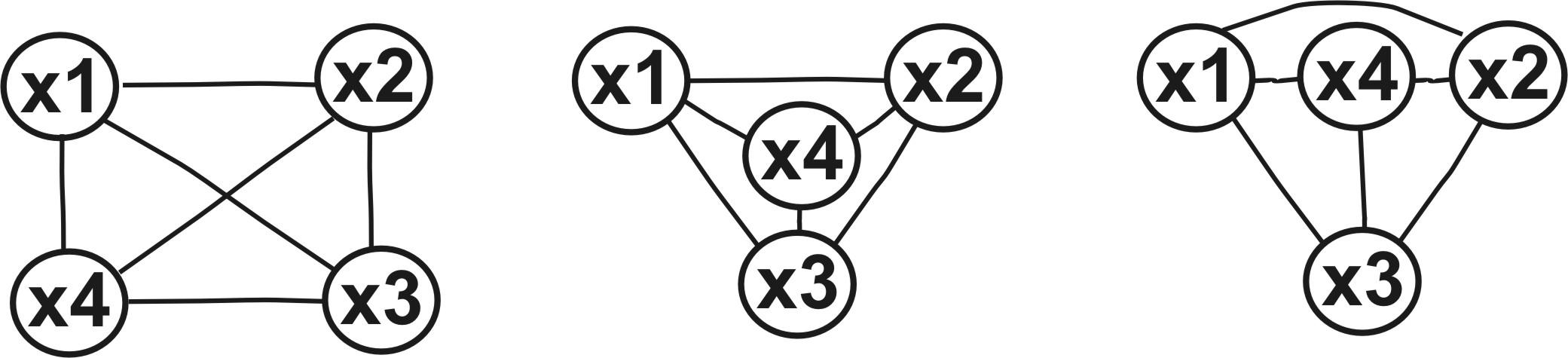
Рис. 14.13. Ізоморфні графи

Принципово можливо в матриці інцидентності визначити також і петлі графу чи орграфу - у цьому випадку для неорієнтованого графу на перетинанні i-го рядка, що відповідає вершині x_i, і j-го стовпця, що відповідає ребру-петлі v_j, ставиться двійка, для орграфу на перетинанні i-го рядка і j-го стовпця необхідно, наприклад, вказати одночасно як +1, так і -1.

Для модифікованої в такий спосіб матриці інцидентності справедливі усі твердження, що стосуються звичайної матриці інцидентності.

Контрольні запитання

1. Як за допомогою двійок визначається граф, чи є таке визначення конструктивним, що дає можливість побудувати граф?

2. Що є неорієнтованим і орієнтованим графуми?

3. Що є ребром, дугою, петлею, рівнобіжними ребрами, строго і нестрого рівнобіжними дугами?

4. Що є ступенем, напівступенем заходу і напівступенем виходу?

5. Що є простим графом, мультиграфом та псевдографом?

6. Яка різниця між порожнім і повним графом?

7. Що є біграфом або двочастковим графом, що є регулярним графом r-го ступеня?

8. Що декларують суміжність та інцидентність, що є позитивною та негативною інцидентністю?

9. Як визначити граф за допомогою трійки, чи є таке завдання конструктивним?

10. Які графи є ізоморфними?