Список літератури Основна

1. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: Наука, 1990. - С.9-19.

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.189-194.

3. Кук Л., Бейз Г. Компьютерная математика. – М.: Наука, 1990, с.217-224.

4. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.89-94.

Додаткова

5. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатоиздат, 1987. - С.67-72.

Для практичних занять

5. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.42-43.

6. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1973. - С.101-124.

Лекція 15. Визначення графів. Зважені графи

Вступ

Лекція має за мету навести додаткові поняття теорії графів. Розглянути визначення маршрутів, ланцюгів, ейлерових та гамільтонових обходів, зв’язності, початкової та скінченної вершин, точок зчленування, дерев, ексцентриситету, радіуса, центра та зважених графів. Звернено увагу до прикладів визначень.

У лекції присутні два підрозділи:

1. Основні визначення (продовження)

2. Зважені (відзначені) графи

15.1. Основні визначення (продовження)

Визначення. Маршрут (шлях) довжини m визначається як послідовність ребер графу, не обов'язково різних, у яких, що граничні вершини двох сусідніх ребер збігаються.

Замкнутий маршрут приводить до тієї ж вершини, з якої він починається. Маршрут позначається як М = <v₁, v₂,…,v_j,…,v_n>...

Приклад. Неорієнтований граф (рис. 21.1.) і можливі маршрути M¹_{x1  x4} = <v1, v2, v3, v2, v4, v5>, M² _{x1  x4}= <v6>

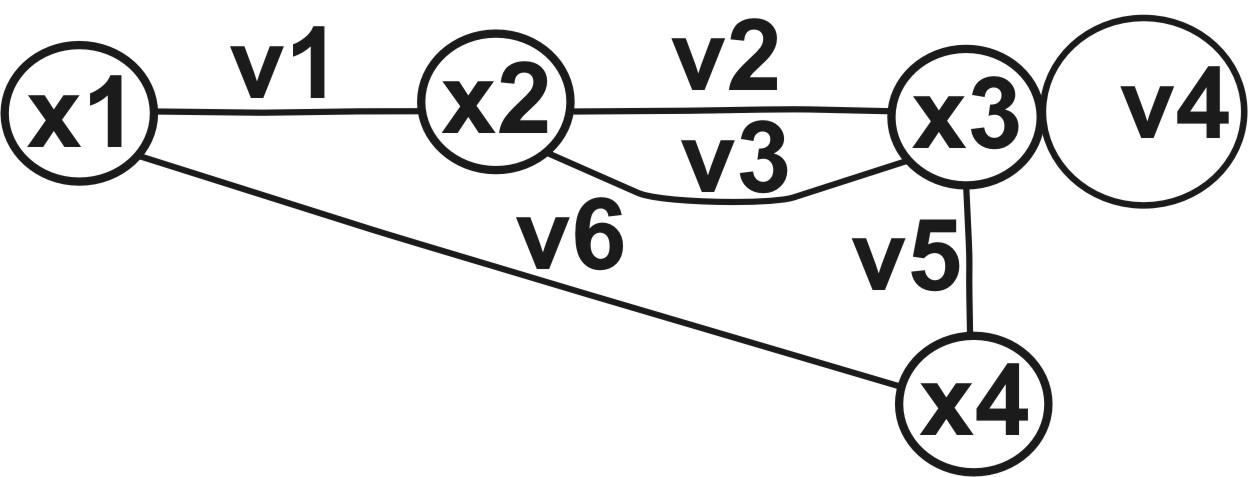
Рис. 15.1. Неорієнтований граф

Визначення. Довжиною маршруту (шляху) М = <v₁, v₂,…,v_j,…,v_n> називається число дуг, що його складують.

Довжина маршруту позначається l(M).

Приклад. Для рис. 15.1. замкнуті маршрути M_{x1  x1} = <v1, v2, v5, v6>; M¹_{x3  x3} = < v4>; M² _{x3  x3}= < v3, v2>.

Визначення. Маршрут, усі ребра якого різні, зветься ланцюгом, маршрут, для якого різні усі вершини, що він проходить, називається простим ланцюгом.

Приклад. Для рис. 15.1. M_{x1  x1} = <v1, v2, v5, v6> і M_{x1  x4} = <v1, v2, v4, v5> - ланцюги, M_{x1  x4} = <v1, v2, v5> - простий ланцюг.

Замкнутий ланцюг звється циклом, замкнутий простий ланцюг називається простим циклом.

Приклад. M_{x1  x1} = <v1, v2, v4, v5, v6> і M_{x3  x3} = <v3, v2, v4> - цикли, M_{x1  x1} = <v1, v2, v5, v6> та M_{x1  x1} = <v3, v2 > - прості цикли.

Визначення. Цикл графу, що містить усі його ребра, називається ейлеревим циклом.

Визначення. Простий цикл графу, що проходить через усі його вершини, називається гамільтоновим циклом.

Ейлерів і гамільтонів цикли (обходи) можливі не для будь-якого графу чи орграфу. В орграфі при визначенні маршруту, ланцюга, циклу, ейлерева і гамільтонова циклу природно враховується напрямок дуг.

Визначення. Частина графу, що містить поряд з деякою підмножиною ребер і всі інцидентні їм вершини, називається підграфом.

Приклад. Граф G = <X, V>, де X = {x1, x2, x3, x4}, V = {v1, v2, v3, v4, v5} і підграф G' = <X’, V'>, де X’ = { x2, x3, x4}, V' = { v2, v3, v4}, G'  G, Х'  X, V'  V.

Рис. 15.2. Граф (ліворуч) і підграф (праворуч)

Визначення. Входом чи початковою вершиною орграфу G = <X, V> є вершина x^(s) X, у якій p(x^(s)) = 0, виходом чи кінцевою вершиною орграфу G = <X, V> є вершина x^(F) X, у якій s(x^(F)) = 0.

Приклад. Початкова вершина x₁ і скінченні вершини x₃, x₅

Рис. 15.3. Початкові і скінченні вершини (х1 – вхід, х3, х5 - вихіди)

В орграфу може бути кілька входів чи виходів (х₅ - другий вихід).

У загальному випадку як вхід чи вихід графу можна розглядати довільну (призначену за якім-небудь критерієм) вершину, а саме, якщо умова входу чи виходу не виконуються, тобто xi(p(xi) = 0) чи xi(s(xi)= = 0), то виводиться фіктивна вершина x^(S) X чи x^(F)  X, що з'єднується єдиною дугою до заданої вершини чи единою дугою із заданої вершини.

Приклад. Уведення фіктивних вершин

Рис. 15.4. Уведення початкової (вхід x_s) і скінченної (вихід x_f) вершин

Шлях від входу орграфу до його виходу, тобто від вершини x^(S) до його вершини x^(F)називається x^(S) - x^(F) - шляхом. Вважається, що хоча б один такий шлях в орграфі існує.

Якщо в орграфі вершини x_i і x_j зв'язані шляхом M[x_i, x_j], то вершина x_j досяжна з вершини x_i чи що вершина x_i досягає вершини x_j.

Дві вершини графу називаються зв'язними, якщо існує маршрут, що їх з'єднує, інакше - незв'язними.

Визначення. Орграф називається міцно зв’язаним, якщо для будь-якої пари його вершин x_i, x_j  X існує орієнтований шлях як з x_i у x_j , так і з x_j у x_i.

Визначення. Граф називається зв'язним, якщо для будь-якої пари його вершин x_i , x_j  X існує шлях з x_i у x_j чи шлях з x_j у x_i.

Визначення. Орграф називається слабо зв’язним, якщо для будь-якої пари його вершин x_i, x_j  X існує така вершина x_k, що x_k досягає як x_i, так і x_j, чи x_k досяжна як з x_j, так і з x_i.

Визначення. Граф, що не є ні міцно зв’язним, ні зв'язним, ні слабо зв’язним називається незв'язаним графом.

Приклад. Зв'язний граф і міцно зв’язний орграф

Рис. 15.5. Зв'язаний граф (ліворуч) і міцно зв'язаний орграф (праворуч)

Якщо існує така вершина, видалення якої перетворює зв'язний граф в незв'язаний, то вона називається точкою зчленування, ребро з такими ж властивостями називається мостом.

Визначення. Граф називається нероздільним, якщо він зв'язний і не має точок зчленування, граф, що має хоча б одну точку зчленування є роздільним і називається сепарабельним.

Приклад. Граф з однією точкою зчленування і граф з одним мостом

Рис. 15.6. Точка зчленування і міст

Зв'язані ациклічні графи називаються деревами. Дерева містять мінімальну кількість ребер, що забезпечує зв'язаність графу. Незв'язаний граф, компонентами якого є дерева, називається лісом.

Приклад. Дерева з різним розгалуженням

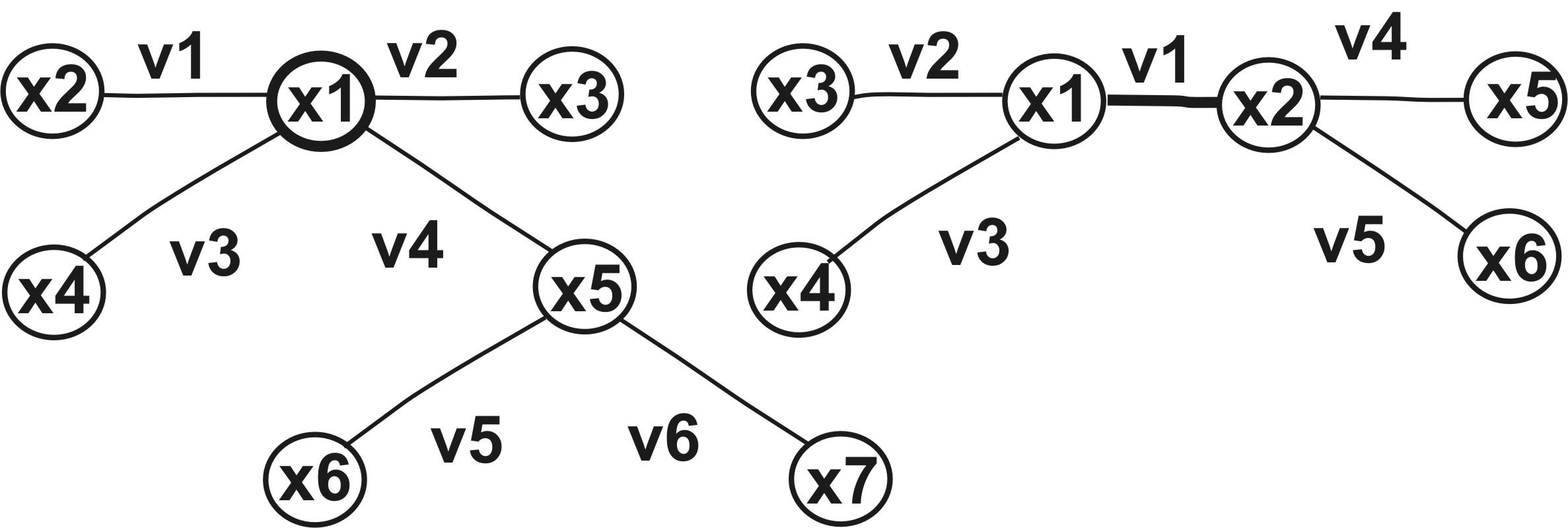
Рис. 15.7. Дерева

Нехай X і V - кількості вершин і ребер. Для дерев справедливо:

X = V + 1; V = X - 1

Визначення. Граф називається плоским (планарним), якщо існує ізоморфний йому граф, що може бути зображений на площині без перетину ребер.

Нехай відстанню d(x₁, x₂) між вершинами x₁, x₂ у дереві (графі) називається довжина мінімального шляху з x₁ у x₂. Відстань від вершини х до найбільш віддаленої від її вершини називається ексцентриситетом е(х) вершини х, тобто

е(х) = max(d(x, y)) = max( d(x, y))

^{y y X}

Найменший з ексцентриситетів називається радіусом r(T) дерева

r(T) = min(e(x)) = min(e(x))

^{x xX}

Центральною вершиною дерева Т називається вершина, у якій ексцентрисітет дорівнює радіусу. Центром дерева називається множина його центральних вершин. Кожне дерево має центр, що складається з однієї вершини чи двох суміжних вершин.

Приклад. r(T) = 3, e(x) = 6 графу

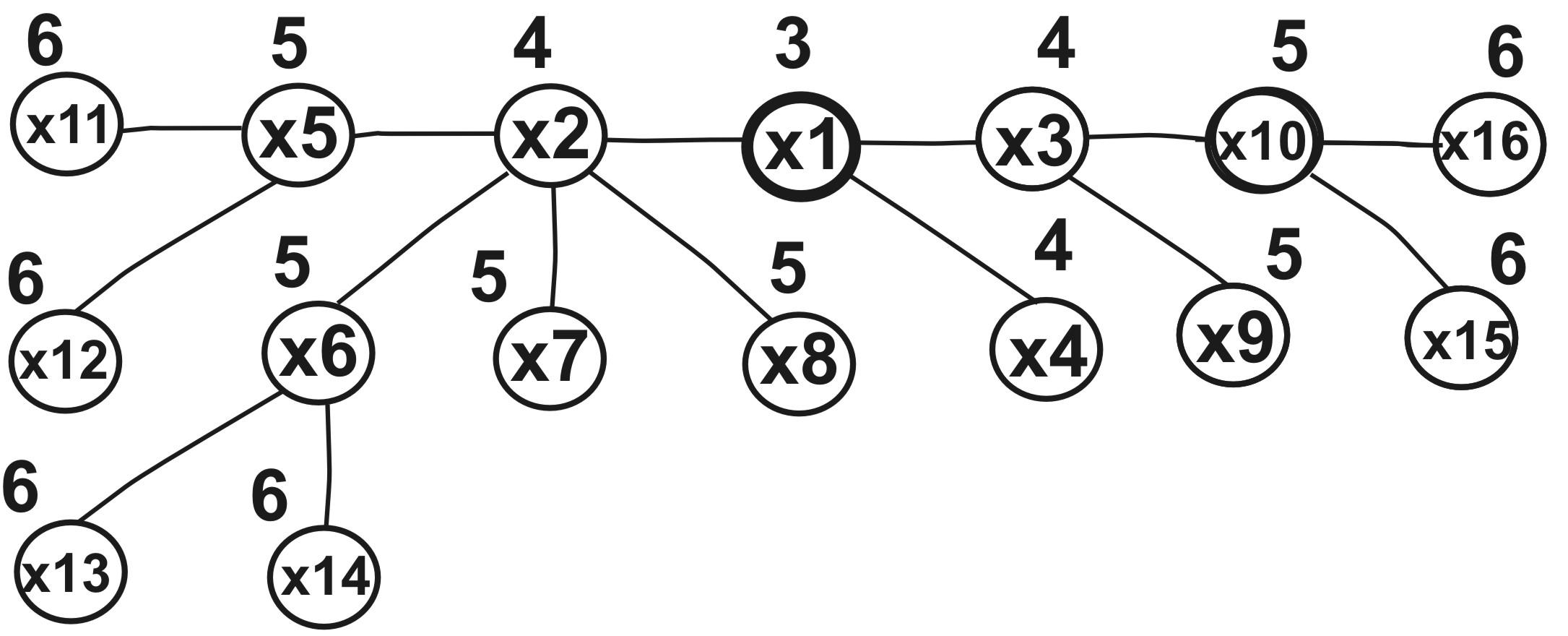
Рис. 15.8. Радіус дерева і ексцентриситети вершин дерева