19.1. Синхронні й асинхронні автомати

Стан s_i автомата А називається стійким, якщо зі стану (s_h, x_j) = s_i при будь-яких x_j випливає співвідношення (s_i, x_j) = s_i. Це означає, що якщо А перейшов у деЯкій стан під дією вхідного сигналу x_j, то вийти з цього стану він може тільки при надходженні на його вхід іншого, відмінного від x_j сигналу.

Автомат Мура називається асинхронним, якщо кожен його стан s_i  S – стійкий. У противному випадку А – синхронний.

Приклад : Асинхронний автомат Мура.

Таблиця 19.1

S X Y	s1 y1	s2 y3	s3 y2
x1	s2	s2	s2
x2	s3	s2	s3
x3	s1	s1	s3

Рис. 19.1. Асинхронний автомат Мура

Визначення. Два автомати з однаковими вхідними алфавітами називаються еквівалентними, якщо після установки їх у початкові стани реакції автоматів на будь-яке вхідне слово збігаються.

Вихідний сигнал Y називається стійким у стані s_h, якщо зі відношення (s_i, x_j) = y_e і (s_i, x_j) = s_h випливає, що (s_h, x_j) = y_e при всіх s_i і x_j, для яких справедливі дві перших рівності.

Автомат Мілі називається асинхронним, якщо всі його стани і вихідні сигнали стійкі, у протилежному випадку він є синхронним.

19.2. Асинхронні автомати, що тактуються

Визначення. Асинхронні автомати, що тактуються, задовольняють умові:

1. вхідний алфавіт Х автомата А розбивається на дві підмножини

X’={х'_1, х'_2,…x’_m} і X’’={х'’_1, х'’_2,…x’’_e};

2. при подачі на А якої-небудь букви х'_j  Х’ існує не менш одного переходу автомата А в будь-якій стан;

3. будь-яка буква х''_j  Х’’ не викликає жодного переходу автомата А в новий стан і на виході з'являється порожній сигнал ”e”;

4. забороняється подача на вхід автомата А послідовностей, будь-які дві поруч розташовані букви яких є літерами підмножини Х’.

Приклад. Вхідна послідовність вигляду <х'₁ х'’₂ х'₂ х'’₁ х'’₃ х'₃ х'’₂ х'₁>.

Приклад. Автомат керування ліфтом, що обслуговує три поверхи. Натискання двох і більш кнопок неприпустимо.

:SXS, :SXY

Таблиця 19.2

S X	s1	s2	s3
x1	s1/ -	s1/y2	s1/y2
x2	s2/y1	s2 / -	s2/y2
x3	s3/y1	s3/y1	s3/ -

Тут y₁- рух нагору, y₂ - рух униз. Усі стани автомата стійкі, але вихідні сигнали – не стійкі, отже, автомат асинхронний.

19.3. Перетворення автоматів Мілі і Мура

Для будь-якого автомата Мура можна побудувати еквівалентний йому автомат Мілі і навпаки.

19.3.1. Перетворення автомата Мура в автомат Мілі

Побудова автомата Мілі виконується на підставі запізнення реакції автомата Мура у порівнянні з автоматом Мілі.

Нехай заданий автомат Мура А_A = (S_A, X_A, Y_A, _A, _A, {s_0A}), еквівалентний йому автомат Мілі А_B = (S_B, X_B, Y_B, _B, _B, {s_0B}) будується в такий спосіб:

S_B : = S_A,

X_B : = X_A,

Y_B : = Y_A,

_B : = _A,

s _0B: = s _0A.

_B будується в такий спосіб, якщо в автоматі Мура (s_і,, x_j) = s_h і _A(s_h) = y_m, то в автоматі Мілі _B(s _і, x_j) = y_m.

При графічному способі завдання автоматів при переході від вихідного автомата Мура до еквівалентного автомата Мілі вихідний сигнал y_m, записаний поруч з вершиною s_h, переноситься на всі дуги, що входять у цю вершину.

При табличному способі завдання автоматів таблиця виходів еквівалентного автомата Мілі виходить з таблиці переходів вихідного автомата Мура заміною символу s_h, що стоіть на перетинанні рядка x_j і стовпця s_i, символом вихідного сигналу y_m, що відрізняє стовпець s_h у таблиці переходів автомата Мура.

Приклад. Вихідний автомат Мура (рис.19.2 ліворуч) і еквівалентний йому автомат Мілі (рис. 19.2 праворуч). Виконано перенос вихідних сигналів з вершин на вхідні в них дуги.

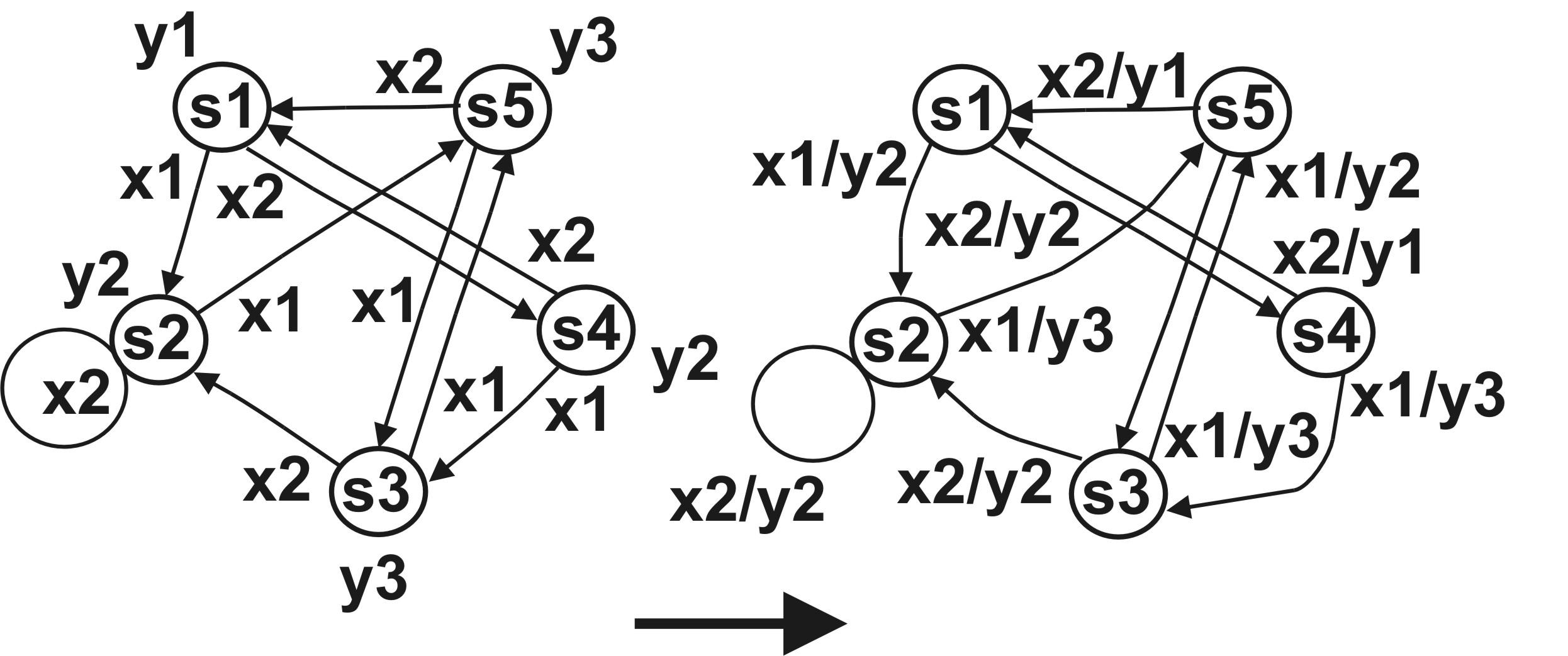
Рис. 19.2. Автомат Мура й еквівалентний йому автомат Мілі