Модуль 6.5. Временны́е характеристики линейных цепей

Цель модуля: знакомство с единичными функциями и их свойствами, нахож дение реакции линейных цепей на воздействие единичных функций, изучение ос новных свойств и методов определения временны́х харктеристик.

Единичные функции и их свойства

Важное место в теории линейных цепей занимает исследование реакции этих цепей на идеализированные внешние воздействия, описываемые так называемыми единичными функциями.

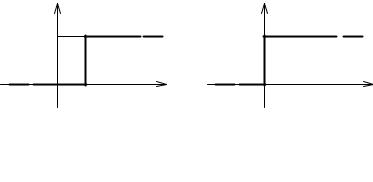
График функции 1(t—t0) имеет вид ступеньки или скачка, высота которого равна 1 (рис. 6.16, а). Скачок такого типа будем называть единичным. При t0 = 0 для единичной ступенчатой функции используют обозначение 1(t) (рис. 6.16, б).

Рис. 6.16. К определению единичной ступенчатой функции

В связи с тем, что произведение любой ограниченной функции, времени f(t) на 1(t—t0) равно нулю при t < t0 и равно f(t) при t ≥ t0:

функцию Хевисайда 1(t — t0) удобно использовать для аналитического представле ния различных внешних воздействий на цепь, значение которых равно нулю до коммутации и скачкообразно изменяется в момент коммутации.

При подключении цепи к источнику постоянного тока или напряжения внеш нее воздействие на цепь

где t0 — момент коммутации.

Внешнее воздействие такого вида называется неединичным скачком. Ис пользуя функцию Хевисайда, выражение (6.95) можно представить в виде

532

·1 .

Если при t = t0 в цепь включается источник гармонического тока или напряже

ния

то внешнее воздействие на цепь можно представить в виде

Если внешнее воздействие на цепь в момент времени t = t0 скачкообразно из меняется от одного фиксированного значения X1 до другого Х2, то

·1 .

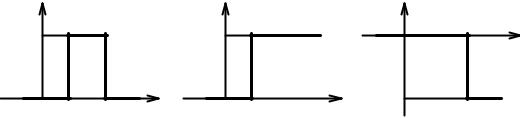
Рис. 6.17. Представление прямоугольного импульса в виде разности двух неединичных скачков

Внешнее воздействие на цепь, имеющее форму прямоугольного импульса вы сотой X и длительностью tИ (рис. 6.17, а), можно представить в виде разности двух одинаковых скачков

·1 ;

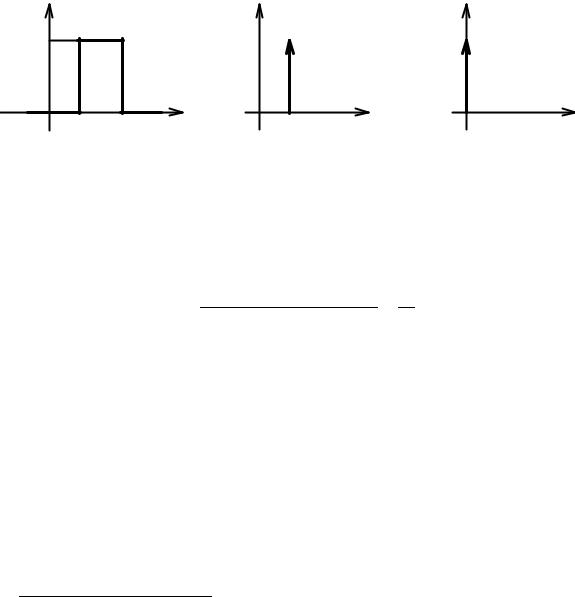
Рассмотрим прямоугольный импульс длительностью t и высотой 1/Δt (рис. 6.18, а). Очевидно, что площадь этого импульса равна 1 и не зависит от t. При уменьшении длительности импульса его высота возрастает, причем при t 0 она стремится к бесконечности, но площадь импульса остается равной 1. Импульс бес конечно малой длительности, бесконечно большой высоты, площадь которого равна

1, будем называть единичным импульсом.

533

Функция, определяющая единичный импульс, обозначается δ(t—t0) и называ ется δ функцией или функцией Дирака*. Таким образом,

причем

При t0 = 0 для δ функции используется обозначение δ(t). При построении вре менны́х диаграмм функции δ(t—t0) и δ(t) будем изображать в виде вертикальной стрелки со значком ∞около острия (рис. 6.18, б, в).

Рис. 6.18. К определению δ функции

Для установления связи между δ функцией и единичной ступенчатой функци ей воспользуемся выражением (6.96). Полагая Х = 1/Δt, и устремляя t к нулю, полу чаем

откуда

Таким образом, δ­функция представляетсобой производную от единичной ступенчатой функции, а единичная ступенчатая функция — интеграл от δ­ функции.

Строгое обоснование операций над единичными функциями, в том числе опе рации дифференцирования единичной ступенчатой функции, дано в теории обоб

*Более строгое определение δ функции см., например, в [12].

534

тации и — момент времени, следующий непосредственно после коммутации. С учетом этого из условия (6.98) можно получить

В общем случае

Произведение произвольной ограниченной функции времени f(t) на δ(t—t0)

Из выражений (6.102) и (6.104) следует, что интеграл от произведения произ вольной ограниченной функции f(t) на δ(t—t0) равен либо значению этой функции при t = t0 (если точка t0 принадлежит интервалу интегрирования), либо нулю (если точка t0 не принадлежит интервалу интегрирования):

Таким образом, с помощью δ функции можно выделять значения функции f(t) в произвольные моменты времени t0. Эту особенность δ функции обычно называют

фильтрующим свойством.

Для определения реакции линейных электрических цепей на внешнее воздей ствие в виде единичного скачка или единичного импульса необходимо найти изо бражения единичных функций по Лапласу. Используя рассмотренные свойства еди ничных функций получаем

d . 6.106

536

При t0 = 0 операторные изображения единичных функций имеют особенно простой вид:

в момент приложения импульса тока скачком увеличивается от начального значе

образом, несмотря на то, что длительность единичного импульса бесконечно мала, он сообщает емкости конечный запас энергии.

Характер зависимостей тока и напряжения от времени не изменится и в том случае, если на емкость подано внешнее воздействие в виде скачка напряжения

и далее сохраняет неизменное значение, а при подключении индуктивности к ис точнику тока iL = j(t) = J ∙1(t) напряжениеиндуктивностиимеетвидбесконечнокороткого

импульса бесконечно большой высоты и конечной площади: .

Скачкообразное (в нарушение законов коммутации) изменение энергии, запа сенной в реактивных элементах цепи, в рассмотренных задачах связано с тем, что в самой постановке этих задач не выполняются исходные положения, принятые при выводе законов коммутации, о том, что токи и напряжения источников энергии не могут достигать бесконечно больших значений.

537