Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт сферы обслуживания и предпринимательства ДГТУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ОТЦ / Start_main1a.pdf

Скачиваний:

590

Добавлен:

09.02.2015

Размер:

15.21 Mб

Скачать

☆

<<< < Предыдущая 39 40 41 42 43 44 45 46 47 48 49 5051 / 16051 52 53 54 55 56 57 58 59 60 61 62 63 > Следующая >>>

arctg .

Нормируя ток I1 по его максимальному значению I0 = E/R, которое достигается при ω = ω0 , и переходя от угловой частоты ω к обобщенной расстройке ξ , оконча тельно получаем

;

arctg .

3.56

Таким образом, зависимость нормированного входного тока контура 1 от час тоты совпадает с нормированной АЧХ входной проводимости контура, а зависи мость начальной фазы ψi от частоты совпадает с нормированной ФЧХ входной про водимости контура смещенной на ψe.

Передаточные характеристики

Найдем коэффициент передачи контура по напряжению для случая, ко гда напряжение снимают с емкости (см. рис. 3.25). При холостом ходе на зажимах 2 — 2' и 3 — 3' ток контура 1 = Y(jω) 1 , где Y(jω)— комплексная входная проводи мость контура, определяемая выражениями (3.46) и (3.47). Выходное напряжение контура

. 3.57

Подставляя (3.57) в (3.44), получаем выражение для коэффициента передачи контура по напряжению

3.58

Умножая числитель и знаменатель (3.58) на ω0 и используя соотношения (3.33), (3.53), преобразуем (3.58) к виду

откуда можно определить модуль (рис. 3.31, а) и аргумент (рис. 3.31, б) комплексно го коэффициента передачи цепи по напряжению:

где	(ω), (ω)		;	2	,	3.59

		— нормированные АЧХ и ФЧХ входной проводимости последователь

ного колебательного контура, определяемые выражениями (3.54).

258

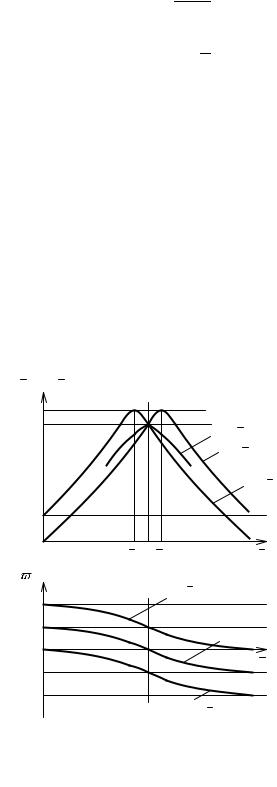
Используя аналогичный подход, находим модуль (рис. 3.31, а) и аргумент (рис. 3.31, б) комплексного коэффициента передачи цепи по напряжению для случая, ко гда напряжение снимают с индуктивности:

где

;	3.60
2 ,

Как следует из определения добротности, на резонансной частоте (ω = ω0) дей ствующее значение напряжения емкости равно действующему значению напряже ния индуктивности и в Q раз превышает напряжение на входе контура, поэтому KL(ω0) = KC(ω0) = Q. При ω = 0 сопротивление емкости бесконечно велико, напряже ние на емкости 2 = 1, напряжение на индуктивности равно нулю. Поэтому

KL (ω= 0) = 0, KC(ω = 0) = 1

На высоких частотах (ω ∞) сопротивление индуктивности бесконечно вели ко, поэтому напряжение 1 оказывается практически полностью приложенным к индуктивности, а напряжение на емкости равно нулю Таким образом, KL (ω= ∞) = 1,

КC (ω = ∞) = 0.

ϑ(ϖ)

Рис. 3.31. АЧХ (а) и ФЧХ (б) коэффициента передачи последовательного колеба тельного контура по напряжению

259

Максимум кривой КC (ω) соответствует частоте, несколько более низкой, а мак симум кривой KL (ω) — частоте, несколько более высокой, чем резонансная. Однако эти смещения максимумов КC (ω) и (ω) относительно резонансной частоты очень малы и на практике ими можно пренебречь. Действительно, исследуя кривые КC (ω) и KL (ω) на экстремум, легко установить, что функция КC (ω) имеет максимум на час тоте

3.61

а функция KL (ω)— на частоте

/ 1

3.62

Подставляя (3.61) и (3.62) в выражения (3.59) и (3.60), находим, что макси мальные значения обеих функций одинаковы:

/ 1

3.63

Анализируя выражения (3.61) — (3.63), нетрудно прийти к заключению, что при Q 5 отличие частот, соответствующих амплитудному критерию резонанса ωL и ωC от ω0, не превышает 0,01 ω0, а Kmax – Q < 0,005Q, поэтому во всех практически важ ных случаях можно считать, что функции КC (ω) и KL(ω) имеют максимум на резо нансной частоте, причем Kmax= Q. Следовательно, в случае высокой добротности ре зонансные частоты, соответствующие амплитудному и фазовому критериям резо нанса, совпадают.

На рис. 3.31, а, который носит чисто качественный характер, смещение кривых KL (ω) и КC (ω) относительно друг друга преувеличено с тем, чтобы показать, что максимумы кривых KL (ω)и КC (ω) находятся на разных частотах. В действительности в узком диапазоне частот, близких к резонансной, когда можно положить ω/ω0 1, эти зависимости почти совпадают друг с другом и с зависимостью Q Y(ω), т. е. KL

(ω) КC (ω) Q (ω).


	Если ко входу последовательного колебательного контура подключить источ
ник напряжения		E , частота	ω	которого изменяется в широких преде

лах,	а действующее значение	и начальная фаза			сохраняют неизменные значе
ния,	то зависимость нормированного выходного				напряжения от частоты при

Q5 будет совпадать с нормированной АЧХ входной проводимости контура:

260

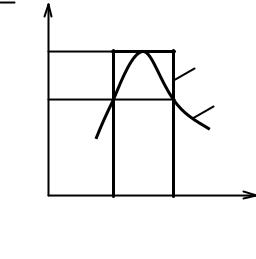
Напомним, что такой же вид имеет зависимость нормированного входного тока контура 1 от частоты ω (3.56).

Таким образом, нормированную входную проводимость контура (ω). можно рассматривать как нормированную реакцию последовательного коле бательного контура на воздействие источника ЭДС с изменяющейся частотой и неизменной амплитудой в режиме холостого хода на зажимах 2 — 2’ и 3 — 3’.

Избирательные свойства последовательного колебательного контура

Важнейшая особенность последовательного колебательного контура заключа ется в том, что амплитуда реакции контура на гармоническое воздействие сущест венно зависит от частоты. На резонансной частоте и в узком диапазоне частот около нее амплитуда отклика достигает наибольшего значения; на частотах, значительно отличающихся от резонансной, амплитуда отклика во много раз меньше макси мального значения. Если на вход такого контура подать сумму гармонических коле баний различных частот, имеющих одинаковые амплитуды, то на выходе можно об наружить, что амплитуда колебаний, частота которых близка к резонансной, значи тельно превышает амплитуду колебаний, частота которых существенно отличается от резонансной. Контур как бы «пропускает» колебания одних частот и «не пропус кает» колебания других частот. Способность электрической цепи выделять колеба ния отдельных частот из суммы колебаний различных частот называется избира

тельностью.

В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой про пускания цепи, и быть равным нулю за пределами этого диапазона. Таким образом, нормированная АЧХ идеальной избирательной цепи должна иметь прямоугольную форму (кривая I на рис. 3.32). АЧХ реальных избирательных цепей, в том числе и АЧХ последовательного колебательного контура (кривая II на рис. 3.32), отличаются от характеристик идеальной избирательной цепи отсутствием резкой границы между диапазонами пропускаемых и задерживаемых (подавляемых) частот. Очевидно, что избирательные свойства реальных цепей тем выше, чем ближе к прямоугольной форма их нормированной АЧХ.

Рис. 3.32. Нормированные АЧХ избирательной цепи

261

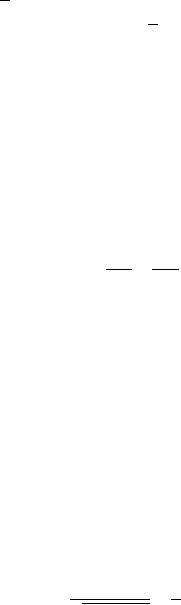
Полоса пропускания (ширина полосы пропускания) реальных избира тельных устройств на уровне 1/α

Π в н

или

Πв н

условно определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает больше, чем в α раз, относительно своего максимального значения. На границах полосы пропускания, т. е. на частотах н и в или н =2π н и в =2π в , амплитуда отклика в α раз меньше своего максимального значения. Чаще всего полосу пропускания избирательной цепи определяют на уровне, когда ампли туда отклика составляет 1/√2 0,707 от максимального значения, а НдБ ―3дб (см.

табл. 3.1). Полосу пропускания цепи на уровне1/√2 обозначим Пf или Пω.

Для оценки избирательных свойств реальной избирательной цепи используют различные параметры, которые оценивают степень отклонения формы ее АЧХ от прямоугольной, в том числе определяют характер изменения АЧХ (неравномерность АЧХ) в пределах полосы пропускания и скорость уменьшения модуля коэффициента передачи (крутизну склонов АЧХ) за пределами или на границе полосы пропускания. В частности, избирательные свойства цепи можно достаточно полно охарактеризо вать с помощью коэффициента прямоугольности АЧХ, который находится как от ношение значений полосы пропускания, измеренных на уровнях 1/α1 и 1/ α 2;

		Π	Π	,	3.64
где α2<α1.		Π	Π	,	3.64
Значения П	или П обычно рассчитывают на уровне 1/100 ( 40 дБ), а значе
					что для идеаль
ния Π или Π	— на уровне 1/√2 (—3 дБ). Нетрудно убедиться,

ной избирательной цепи коэффициент прямоугольности АЧХ равен единице при любом выборе α1 и α2, а для реальной избирательной цепи он всегда больше единицы. Очевидно, что избирательные свойства цепи тем выше, чем ближе к еди нице значения К .

Избирательные свойства последовательного колебательного контура(ξ).						опреде
ляются формой нормированнойξ				АЧХ входной проводимости контура		Полагая
в выражении (3.54)	=	гр ,,	(	α,	получаем
				гр) =1/

1 1 ,

1гр

262

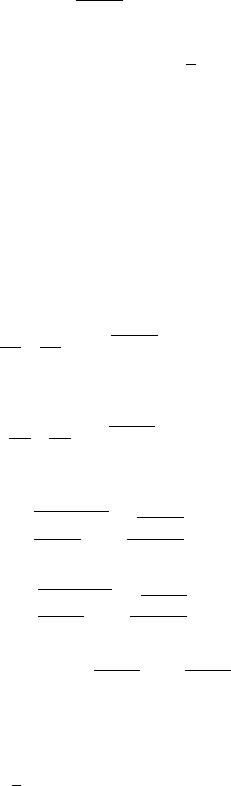
откуда

гр

3.65

Как следует из выражения (3.65), абсолютное значение обобщенной расстрой

ки на границах полосы пропускания на уровне ½, т е. при

α=

√2,

равно единице; при

этом

на нижней

границе полосы пропускания

√

1, а на верхней

гр

√

1. Из выражений (3.51), (3.54) и (3.65) следует, что на границах полосы

гр

пропускания

на

уровне 1/√2

аргумент входной

проводимости контура равен

ГР

/4 (см. рис. 3.29), а реактивная составляющая входного сопротивления кон

тура

x = ωL —

/(ωС)

по абсолютному значению — сопротивлению потерь

Используя полученные результаты, найдем полосу пропускания последова

тельного колебательного контура на произвольном уровне 1/

и коэффициент пря

моугольности АЧХ входной проводимости контура. Полагая в выражении (3.51)

гр ,	ω	= н и	гр ,	ω	= в	, получим

н1 ;

в1 ,

откуда

4	1	1	√	2	1	;			3.66
4	1	1	√	2	1	;			3.67
Π			1				1	.	3.68
Π			1				1	.	3.68

Из выражений (3.66) — (3.68) следует, что полоса пропускания контура при фиксированном значении резонансной частоты ω0 обратно пропорциональна его добротности и не зависит от емкости С, а полоса пропускания последовательного колебательного контура на уровне 1/√2 = 0,707 в Q раз меньше его резонансной час тоты:

Π Π√				,	3.69

263

Π Π√				.	3.70

Согласно выражению (3.68), полоса пропускания последовательного колеба тельного контура на уровне 1/100


Π	100 1 100	3.71
Π	100 1 100	3.71

и коэффициент прямоугольности АЧХ его входной проводимости

Π√

100 .

Таким образом, коэффициент прямоугольности АЧХ контура оказывается на много большим единицы, что свидетельствует о том, что избирательные свойства последовательного колебательного контура далеки от свойств идеальной избира тельной цепи.

В связи с тем, что	ω
	2(—) — это нормированный отклик контура в режиме холо
стого хода на зажимах	2'	и	3 — 3'		на внешнее гармоническое1воздействие, зада
ваемое источником напряжения,				подключенным к зажимам		— 1'	, выражения

(3.68) — (3.71) позволяют определить избирательность колебательного контура только в том случае, когда внутреннее сопротивление источника энергии равно ну лю, а входное сопротивление нагрузки, подключенной к зажимам 2 — 2' или 3 — 3', бесконечно велико. Рассмотрим влияние внутреннего сопротивления источника энергии и сопротивления нагрузки на избирательные свойства последовательного колебательного контура.

Пусть контур подключен к источнику энергии с конечным внутренним сопро тивлением (рис. 3.33, а). Очевидно, что включенные последовательно сопротив ления и R можно заменить сопротивлением Rэк = + R. При этом рассматриваемая схема преобразуется в схему, приведенную на рис. 3.23, б; она может быть описана соотношениями, полученными на основании анализа этой схемы при замене R на Rэк. В частности, добротность такого контура (будем называть ее эквивалентной доб ротностью последовательного колебательного контура) определяется выражением

эк , 3.72

эк 1

где Q = ρ/R — добротность контура без учета сопротивления источника.

Ширина полосы пропускания контура с учетом внутреннего сопротивления ис точника энергии может быть найдена из выражения(3.69) при замене Q на Qэк1:

Π				1		3.73

эк

264

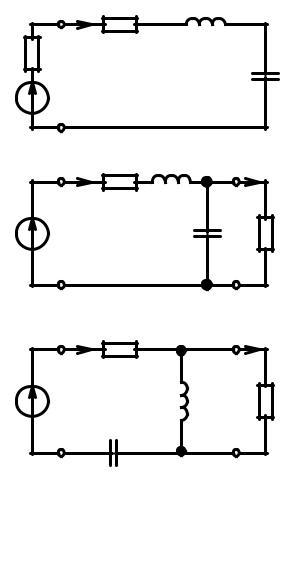
Как следует из выражений (3.72), (3.73), наличие внутреннего сопротивления источника энергии уменьшает эквивалентную добротность контура и увеличивает ширину его полосы пропускания. Поэтому для повышения эквивалентной добротно сти контура желательно, чтобы источник энергии, к которому подключен контур, имел бы как можно меньшее внутреннее сопротивление, т. е. по свойствам прибли жался к идеальному источнику напряжения.

Рис. 3.33. К учету влияния внутреннего сопротивления источника и сопротивления нагрузки на избирательные свойства последовательного колебательного контура

Пусть к зажимам 2 — 2' или 3 — 3' последовательного колебательного контура подключена нагрузка (рис. 3.33, б, в) так, что ток 2 или 3 не равен нулю. Очевидно, что сопротивление нагрузки, подключенное параллельно емкости или индуктивно сти, влияет на работу контура таким же образом, как сопротивления RC пар и RL пар, входящие в параллельные схемы замещения конденсатора и индуктивной катушки.

Ранее отмечалось, что параллельные схемы замещения элементов могутСбыть заме

нены последовательными, причем приC

высокойL

добротности элементов пар

посл=

С, L

пар

посл=C

, а сопротивленияL

посл и

посл обратно пропорциональны сопро

тивлениям

пар (3.22) и

пар (3.20). Таким образом, сопротивления нагрузки

н2,

265

<<< < Предыдущая 39 40 41 42 43 44 45 46 47 48 49 5051 / 16051 52 53 54 55 56 57 58 59 60 61 62 63 > Следующая >>>

Соседние файлы в папке ОТЦ

#
09.02.2015932.3 Кб45Lab_rab_df.pdf
#
09.02.20152.5 Mб64RGZ21.doc
#
09.02.201515.21 Mб590Start_main1a.pdf