
- •Аннотация
- •Оглавление
- •Дорогие читатели!
- •Предисловие
- •Введение
- •Книга 1. Основные понятия теории цепей
- •Модуль 1.1. Основные определения
- •Электрическая цепь
- •Электрический ток
- •Напряжение
- •Электродвижущая сила
- •Мощность и энергия
- •Схема электрической цепи
- •Вопросы для самопроверки
- •Модуль 1.2. Идеализированные пассивные элементы
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Дуальные элементы и цепи
- •Схемы замещения реальных элементов электрических цепей
- •Вопросы для самопроверки
- •Задачи
- •Модуль 1.3. Идеализированные активные элементы
- •Идеальный источник напряжения
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.4. Топология цепей
- •Схемы электрических цепей. Основные определения
- •Понятие о компонентных и топологических уравнениях. Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.5. Уравнения электрического равновесия цепей
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Классификация электрических цепей
- •Вопросы для самопроверки
- •Ответы
- •Модуль 2.1. Анализ линейных цепей с источниками гармонических токов и напряжений
- •Понятие о гармонических функциях
- •Линейные операции над гармоническими функциями
- •Среднее, средневыпрямленное и действующее значения гармонических токов и напряжений
- •Дифференциальное уравнение цепи при гармоническом воздействии
- •Вопросы для самопроверки
- •Модуль 2.2. Метод комплексных амплитуд
- •Понятие о символических методах
- •Комплексные числа и основные операции над ними
- •Операции над комплексными изображениями гармонических функций
- •Комплексные сопротивление и проводимость пассивного участка цепи
- •Порядок анализа цепи методом комплексных амплитуд
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.3. Идеализированные пассивные элементы при гармоническом воздействии
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Делители напряжения и тока
- •Вопросы для самопроверки
- •Задачи
- •Мгновенная мощность пассивного двухполюсник
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Коэффициент мощности
- •Согласование источника энергии с нагрузкой
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.6. Преобразования электрических цепей
- •Понятие об эквивалентных преобразованиях
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное преобразование
- •Комплексные схемы замещения источников энергии
- •Перенос источников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.7. Цепи с взаимной индуктивностью
- •Понятие о взаимной индуктивности
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Понятие о линейных трансформаторах
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 3. Частотные характеристики и резонансные явления
- •Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики цепей с одним реактивным элементом
- •Понятие о резонансе в электрических цепях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.2. Последовательный колебательный контур
- •Cхемы замещения и параметры элементов контура
- •Энергетические процессы в последовательном колебательном контуре
- •Входные характеристики
- •Передаточные характеристики
- •Избирательные свойства последовательного колебательного контура
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.3. Параллельный колебательный контур
- •Схемы замещения
- •Параллельный колебательный контур основного вида
- •Параллельный колебательный контур с разделенной индуктивностью
- •Параллельный колебательный контур с разделенной емкостью
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.4. Связанные колебательные контуры
- •Общие сведения
- •Схемы замещения
- •Настройка связанных контуров
- •Частотные характеристики
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Общие сведения
- •Методы, основанные на непосредственном применении законов Кирхгофа
- •Метод контурных токов
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.2. Основные теоремы теории цепей
- •Принцип наложения
- •Теорема взаимности
- •Теорема компенсации
- •Автономные и неавтономные двухполюсники
- •Теорема об эквивалентном источнике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.3. Метод сигнальных графов
- •Общие сведения
- •Преобразования сигнальных графов
- •Применение сигнальных графов к анализу цепей
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 5. Нелинейные резистивные цепи
- •Модуль 5.1. Постановка задачи анализа нелинейных резистивных цепей
- •Вводные замечания
- •Нелинейные резистивные элементы
- •Уравнения электрического равновесия нелинейных резистивных цепей
- •Вопросы для самопроверки
- •Модуль 5.2. Графические методы анализа нелинейных резистивных цепей
- •Простейшие преобразования нелинейных резистивных цепей
- •Определение рабочих точек нелинейных резистивных элементов
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Задача аппроксимации
- •Выбор аппроксимирующей функции
- •Определение коэффициентов аппроксимирующей функции
- •Вопросы для самопроверки
- •Задачи
- •Нелинейное сопротивление при гармоническом воздействии
- •Понятие о режимах малого и большого сигнала
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 6. Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами
- •Модуль 6.1. Задача анализа переходных процессов
- •Возникновение переходных процессов. Понятие о коммутации
- •Законы коммутации
- •Общий подход к анализу переходных процессов
- •Определение порядка сложности цепи
- •Вопросы для самопроверки
- •Модуль 6.2. Классический метод анализа переходных процессов
- •Свободные и вынужденные составляющие токов и напряжений
- •Порядок анализа переходных процессов классическим методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.3. Операторный метод анализа переходных процессов
- •Преобразование Лапласа и его применение к решению дифференциальных уравнений
- •Порядок анализа переходных процессов операторным методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.4. Операторные характеристики линейных цепей
- •Реакция цепи на экспоненциальное воздействие
- •Понятие об операторных характеристиках
- •Методы определения операторных характеристик
- •Дифференцирующие и интегрирующие цепи
- •Вопросы для самопроверки
- •Единичные функции и их свойства
- •Переходная и импульсная характеристики линейных цепей
- •Методы определения временных характеристик
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Определение реакции цепи на произвольное внешнее воздействие
- •Определение реакции цепи на произвольное внешнее воздействие по ее переходной характеристике
- •Определение реакции цепи на произвольное внешнее воздействие по ее импульсной характеристике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 7. Основы теории четырехполюсников и многополюсников
- •Модуль 7.1. Многополюсники и цепи с многополюсными элементами
- •Задача анализа цепей с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Классификация проходных четырехполюсников
- •Основные уравнения и первичные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров неавтономных проходных четырехполюсников
- •Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.4. Невзаимные проходные четырехполюсники
- •Идеальные усилители напряжения и тока
- •Однонаправленные цепи и цепи с обратной связью
- •Идеальные операционные усилители
- •Преобразователи сопротивления
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.5. Электрические фильтры
- •Классификация электрических фильтров
- •Реактивные фильтры
- •Активные фильтры
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 8. Цепи с распределенными параметрами
- •Модуль 8.1. Задача анализа цепей с распределенными параметрами
- •Общие сведения
- •Общее решение дифференциальных уравнений длинной линии
- •Вопросы для самопроверки
- •Волновые процессы в однородной длинной линии
- •Режим стоячих волн
- •Режим смешанных волн
- •Вопросы для самопроверки
- •Задачи
- •Проходной четырехполюсник с распределенными параметрами
- •Входное сопротивление отрезка однородной длинной линии
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Распределение напряжения и тока в однородной линии без потерь при произвольном внешнем воздействии
- •Вопросы для самопроверки
- •Задачи
- •Модуль 8.5. Цепи с распределенными параметрами специальных типов
- •Резистивные линии
- •Неоднородные линии
- •Вопросы для самопроверки
- •Задачи
- •Ответы
- •Книга 9. Синтез электрических цепей
- •Модуль 9.1. Задача синтеза линейных электрических цепей
- •Понятие физической реализуемости
- •Основные этапы синтеза цепей
- •Вопросы для самопроверки
- •Понятие о положительных вещественных функциях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.3. Методы реализации реактивных двухполюсников
- •Методы выделения простейших составляющих (метод Фостера)
- •Метод разложения в цепную дробь (метод Кауэра)
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.4. Основы синтеза линейных пассивных четырехполюсников
- •Задача синтеза четырехполюсников
- •Методы реализации пассивных четырехполюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 10. Методы автоматизированного анализа цепей
- •Модуль 10.1. Задача автоматизированного анализа цепей
- •Понятие о ручных и машинных методах анализа цепей
- •Общие представления о программах машинного анализа цепей
- •Вопросы для самопроверки
- •Топологические матрицы и топологические уравнения
- •Свойства топологических матриц
- •Компонентные матрицы и компонентные уравнения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Методы узловых напряжений и контурных токов
- •Метод переменных состояния
- •Формирование уравнений состояния в матричной форме
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 10.4. Особенности современных программ автоматизированного анализа цепей
- •Выбор методов формирования уравнений электрического равновесия. Понятие о поколениях программ автоматизированного анализа цепей
- •Вопросы для самопроверки
- •Ответы
- •Заключение
- •Приложения
- •Приложение 1. Таблица оригиналов и изображений по Лапласу
- •Приложение 2. Основные уравнения проходных четырёхполюсников
- •Приложение 3. Соотношения между первичными параметрами проходных четырехполюсников
- •Приложение 5. Соотношения между первичными параметрами взаимных и симметричных четырехполюсников
- •Приложение 6. Приставки для образования кратных и дольных единиц
- •Приложение 7. Инструкция для работы с Самоучителем по курсу «Основы теории цепей»
- •Список литературы
не может быть использован для анализа цепей со взаимной индуктивностью при kM = 1.
Формирование уравнений электрического равновесия цепей с зависимыми источниками
Основная проблема, возникающая при формировании уравнений электриче ского равновесия цепей с управляемыми источниками, заключается в том, что в этих уравнениях могут появляться новые переменные, не входящие в выбранную систе му независимых переменных, представляющие собой управляющие токи или на пряжения источников. Обычно эта проблема решается одним из двух способов:
1)введением дополнительных уравнений, выражающих управляющие токи или напряжения через величины, выбранные в используемом методе анализа в ка честве независимых переменных;
2)преобразованием исходной цепи, направленным на замену заданных управ ляемых источников другими источниками, управляемыми токами или напряже ниями, выбранными в качестве независимых переменных.
При формировании уравнений различают зависимые источники, управляемые током или напряжением какой либо невырожденной, т. е не содержащей источни ков тока и не составленной только из источников напряжения, ветви, и источники, у которых управляющее воздействие не является током или напряжением какой либо невырожденной ветви.
Рассмотрим сначала методику формирования уравнений электрического рав новесия цепей, содержащих зависимые источники первого типа. Особенностью та ких цепей является возможность преобразования источников, управляемых напря жением какой либо ветви в источники, управляемые током этой же ветви, и наобо рот.
Пусть в исследуемой цепи имеются источники напряжения и тока, управляе мые напряжением a й ветви:
К S |
; |
, |
4.21 |
где , |
— коэффициенты управления источников. |
а в соотношениях |
|
Используя компонентное уравнение а й |
аветви, напряжение |
||
(4.21) можно выразить через ток этой ветви |
, при этом источник, управляемый на |
||
пряжением, преобразуется в источник, управляемый током. В простейшем случае связь напряжения и тока а й ветви описывается законом Ома в комплексной форме:
. 4.22
Подставляя (4.22) в (4.21), получаем
;.
330

Аналогичным образом можно преобразовать источники, управляемые током какой либо ветви, в источники, управляемые напряжением этой же ветви.
При составлении основной системы уравнений электрического равновесия це пей, содержащих зависимые источники напряжения или тока рассматриваемого ти па, эти источники учитывают в уравнениях, составленных на основании законов Кирхгофа, наряду с независимыми источниками, а затем токи и ЭДС зависимых ис точников выражают через соответствующие управляющие воздействия. В связи с тем что управляющие воздействия представляют собой токи и напряжения ветвей цепи, в основной системе уравнений электрического равновесия цепи не появится новых неизвестных токов или напряжений. При формировании уравнений электри ческого равновесия цепи по методу ТВ задающие токи и ЭДС управляемых источни ков должны быть выражены через неизвестные токи а при формировании таких уравнений по методу НВ — через известные напряжения ветвей.
Пример4.7.Используя метод токов ветвей, составим уравнения электрического равновесия цепи рис. 4.2, а при условии, что ток источника тока является, функцией на пряжения ветви, содержащей индуктивность: S 3.
Задача решается в два этапа. На первом формируют систему уравнений по методу ТВ, в которой ток источника учитывается так же, как если бы это был ток независимого источника см. пример 4.2 :
0; |
0; |
; |
0. |
|
0; |
|
|
На втором этапе ток управляемого источника выражают через ток третьей ветви S 3 Z3S 3 и подставляют в полученную систему уравнений:
|
0; |
; |
0. |
|
0; |
0; |
|
Таким образом, получаем систему из пяти уравнений для определения пяти неиз |
|||
вестных токов ветвей, после решения которой и расчета тока |
3, находят ток управляемого |
||
источника |
и напряжения всех ветвей. |
|
|
Метод контурных токов позволяет сформировать систему уравнений электри ческого равновесия цепи, содержащей зависимые источники напряжения, управ ляемые током. Если в цепь входят также зависимые источники других типов, то они должны быть преобразованы в источники напряжения, управляемые током. При со ставлении контурных уравнений ЭДС таких источников учитываются наравне с ЭДС независимых источников, а затем переносятся в левую часть уравнений и выража ются через соответствующие контурные токи. Таким образом, наличие в исследуе мой цепи источников ЭДС, управляемых током, приводит к изменению коэффициен тов перед некоторыми из контурных токов и может обусловить несимметричность матрицы контурных сопротивлений относительно главной диагонали.
331

Пример4.8.Составим систему контурных уравнений цепи рис. 4.2 при условии,
что ток источника тока является функцией напряжения на сопротивлении Z3: |
S 3. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.6. К примеру 4.8
Преобразуем схему цепи таким образом, чтобы управляемый напряжением источ ник тока был заменен на управляемый током источник напряжения рис. 4.6,а
.
Выбрав систему независимых контуров рис. 4.6, б , составим систему контурных уравнений цепи, в которой ЭДС источника учтена так, как будто этот источник независи мый:
где |
11 2 ; |
|
|
; |
22 |
4 |
, |
||
Перенося ЭДС |
в левую часть контурных уравнений и выражая ее через контур |
|||
ные токи |
Zm 3 |
Zm |
11 |
22 , получаем |
;
0.
Матрица контурных сопротивлений данной цепи несимметрична относительно главной диагонали:
.
Метод узловых напряжений позволяет составить систему уравнений электри ческого равновесия цепей, содержащих управляемые напряжением источники тока. Если цепь содержит зависимые источники других типов, то они должны быть заме нены на источники тока, управляемые напряжением. При составлении узловых уравнений токи таких источников учитывают наравне с токами независимых ис точников, а затем выражают через соответствующие узловые напряжения. Наличие в рассматриваемой цепи управляемых источников, как правило, приводит к тому, что матрица узловых проводимостей цепи становится несимметричной относитель но главной диагонали.
Пример4.9.Составим узловые уравнения цепи рис. 4.2, а при условии , что ЭДС ис точника напряжения является функцией тока 4: Zn 4.
332
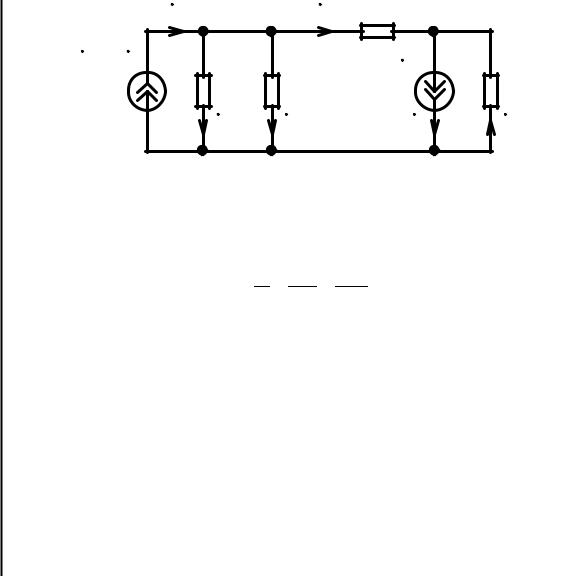
Рис. 4.7. К примеру 4.9
Преобразуем схему цепи таким образом, чтобы управляемый током источник ЭДС был заменен на управляемый напряжением источник тока 2 рис.4.7
.
Составляем узловые уравнения преобразованной цепи, учитывая ток управляемого источника 2 наравне с током независимого источника 1:
Перенося ток управляемого источника |
. |
; |
2 в левую часть узловых уравнений и вы |
||
ражая его через узловые напряжения 2 Yn 4 |
Yn 20 30 , получаем |
|
|
|
0; |
|
|
. |
Как и следовало ожидать, матрица узловых проводимостей рассматриваемой цепи несимметрична относительно главной диагонали:
.
Рассмотрим особенности формирования уравнений электрического равновесия цепей, содержащих зависимые источники, у которых управляющее воздействие не является током или напряжением какой либо невырожденной ветви. Можно выде лить три случая: 1) источники, управляемые токами независимых источников тока или напряжениями независимых источников напряжения; 2) источники, управляе мые токами независимых источников напряжения и напряжениями независимых источников тока; 3) источники, у которых управляющие токи или напряжения не являются токами или напряжениями каких либо ветвей цепи.
Наличие в цепи источников, управляемых токами источников тока и напряже ниями источников напряжения, не приводит к появлению в уравнениях электриче ского равновесия новых переменных, поскольку управляющие воздействия у таких источников являются заданными величинами. Источники такого типа учитываются в уравнениях электрического равновесия так же, как и независимые источники.
Если исследуемая цепь содержит источники, управляемые напряжением ветви, содержащей источники тока, то вследствие отсутствия непосредственной зависимо сти между током и напряжением вырожденной ветви они не могут быть преобразо
333
ваны в источники, управляемые током этой же ветви. Аналогично этому, источники, управляемые током ветви, составленной только из источников напряжения, не мо гут быть преобразованы в источники, управляемые напряжением этой же ветви. В этом случае для изменения вида управляющего воздействия это воздействие снача ла должно быть выражено через токи или напряжения невырожденных ветвей. (На помним, что напряжение на источнике тока может быть выражено через напряже ния ветвей дерева, входящих в главный контур, замыкаемой ветвью с этим источни ком, а ток ветви, составленной только из источников напряжения,— через токи главных ветвей, входящих в соответствующее главное сечение.)
Рис 4.8. Введение в цепь вырожденной ветви, соответствующей управляющему напряжению
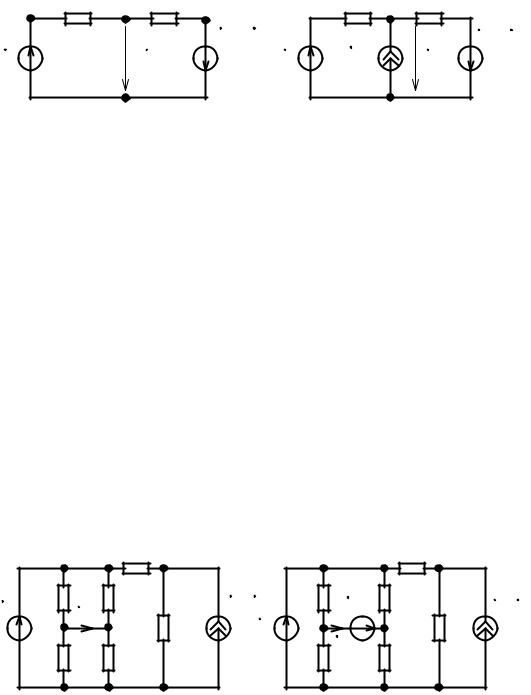
Если цепь содержит зависимые источники, управляющие токи или напряжения которых не являются токами или напряжениями ветвей этой цепи, то при составле нии системы уравнений электрического равновесия обязательно появятся дополни тельные неизвестные — соответствующие управляющие токи или напряжения. Для того чтобы получить достаточное число уравнений для определения всех неизвест ных токов и напряжений, в состав рассматриваемых цепей обычно включают допол нительные вырожденные ветви, соответствующие управляющим воздействиям за висимых источников. Так, если в цепи (рис. 4.8, а) имеется источник напряжения, ЭДС которого зависит от напряжения упр, не являющегося напряжением какой либо ветви, то для составления основной системы уравнений электрического равновесия эту цепь дополняют вырожденной ветвью (рис. 4.8, б), содержащей независимый ис точник тока = 0, напряжение которого равно упр. Если электрическая цепь содер жит зависимый источник тока , управляемый током упр, не являющимся током ка кой либо ветви (рис. 4.9, а), то для составления основной системы уравнений элек
трического равновесия эту цепь следует дополнить вырожденной, |
ветвью, содержа |
||
щей независимый источник напряжения = 0 (рис. 4.9 |
б |
), ток которого равен упр. |
|
|
|||
|
|
(1) |
Z5 |
(2) |
|
E1 |
|
Z1 |
Z3 |
|
J=KIупр |
|
Iупр |
|
|
||
(3) |
|
Z6 |
E1 |
||
|
|
|
|||
|
|
Z2 |
Z4 |
|
|
|
|
|
(0) |
|
|
334 |
|
|
a) |
|
|
|
|
|
|
|
|
(1) |
Z5 |
(2) |
|
Z1 |
E2=0 |
Z3 |
J=KIупр |
|
(3) |
(4) |
|||
Iупр |
Z6 |
|||
Z2 |
Z4 |
|
||
|
|
|||
|
|
(0) |
|
|
|
|
б) |
|
