
- •Аннотация
- •Оглавление
- •Дорогие читатели!
- •Предисловие
- •Введение
- •Книга 1. Основные понятия теории цепей
- •Модуль 1.1. Основные определения
- •Электрическая цепь
- •Электрический ток
- •Напряжение
- •Электродвижущая сила
- •Мощность и энергия
- •Схема электрической цепи
- •Вопросы для самопроверки
- •Модуль 1.2. Идеализированные пассивные элементы
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Дуальные элементы и цепи
- •Схемы замещения реальных элементов электрических цепей
- •Вопросы для самопроверки
- •Задачи
- •Модуль 1.3. Идеализированные активные элементы
- •Идеальный источник напряжения
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.4. Топология цепей
- •Схемы электрических цепей. Основные определения
- •Понятие о компонентных и топологических уравнениях. Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 1.5. Уравнения электрического равновесия цепей
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Классификация электрических цепей
- •Вопросы для самопроверки
- •Ответы
- •Модуль 2.1. Анализ линейных цепей с источниками гармонических токов и напряжений
- •Понятие о гармонических функциях
- •Линейные операции над гармоническими функциями
- •Среднее, средневыпрямленное и действующее значения гармонических токов и напряжений
- •Дифференциальное уравнение цепи при гармоническом воздействии
- •Вопросы для самопроверки
- •Модуль 2.2. Метод комплексных амплитуд
- •Понятие о символических методах
- •Комплексные числа и основные операции над ними
- •Операции над комплексными изображениями гармонических функций
- •Комплексные сопротивление и проводимость пассивного участка цепи
- •Порядок анализа цепи методом комплексных амплитуд
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.3. Идеализированные пассивные элементы при гармоническом воздействии
- •Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Делители напряжения и тока
- •Вопросы для самопроверки
- •Задачи
- •Мгновенная мощность пассивного двухполюсник
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Коэффициент мощности
- •Согласование источника энергии с нагрузкой
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.6. Преобразования электрических цепей
- •Понятие об эквивалентных преобразованиях
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное преобразование
- •Комплексные схемы замещения источников энергии
- •Перенос источников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 2.7. Цепи с взаимной индуктивностью
- •Понятие о взаимной индуктивности
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Понятие о линейных трансформаторах
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 3. Частотные характеристики и резонансные явления
- •Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики цепей с одним реактивным элементом
- •Понятие о резонансе в электрических цепях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.2. Последовательный колебательный контур
- •Cхемы замещения и параметры элементов контура
- •Энергетические процессы в последовательном колебательном контуре
- •Входные характеристики
- •Передаточные характеристики
- •Избирательные свойства последовательного колебательного контура
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.3. Параллельный колебательный контур
- •Схемы замещения
- •Параллельный колебательный контур основного вида
- •Параллельный колебательный контур с разделенной индуктивностью
- •Параллельный колебательный контур с разделенной емкостью
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 3.4. Связанные колебательные контуры
- •Общие сведения
- •Схемы замещения
- •Настройка связанных контуров
- •Частотные характеристики
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Общие сведения
- •Методы, основанные на непосредственном применении законов Кирхгофа
- •Метод контурных токов
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.2. Основные теоремы теории цепей
- •Принцип наложения
- •Теорема взаимности
- •Теорема компенсации
- •Автономные и неавтономные двухполюсники
- •Теорема об эквивалентном источнике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 4.3. Метод сигнальных графов
- •Общие сведения
- •Преобразования сигнальных графов
- •Применение сигнальных графов к анализу цепей
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 5. Нелинейные резистивные цепи
- •Модуль 5.1. Постановка задачи анализа нелинейных резистивных цепей
- •Вводные замечания
- •Нелинейные резистивные элементы
- •Уравнения электрического равновесия нелинейных резистивных цепей
- •Вопросы для самопроверки
- •Модуль 5.2. Графические методы анализа нелинейных резистивных цепей
- •Простейшие преобразования нелинейных резистивных цепей
- •Определение рабочих точек нелинейных резистивных элементов
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Задача аппроксимации
- •Выбор аппроксимирующей функции
- •Определение коэффициентов аппроксимирующей функции
- •Вопросы для самопроверки
- •Задачи
- •Нелинейное сопротивление при гармоническом воздействии
- •Понятие о режимах малого и большого сигнала
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 6. Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами
- •Модуль 6.1. Задача анализа переходных процессов
- •Возникновение переходных процессов. Понятие о коммутации
- •Законы коммутации
- •Общий подход к анализу переходных процессов
- •Определение порядка сложности цепи
- •Вопросы для самопроверки
- •Модуль 6.2. Классический метод анализа переходных процессов
- •Свободные и вынужденные составляющие токов и напряжений
- •Порядок анализа переходных процессов классическим методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.3. Операторный метод анализа переходных процессов
- •Преобразование Лапласа и его применение к решению дифференциальных уравнений
- •Порядок анализа переходных процессов операторным методом
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 6.4. Операторные характеристики линейных цепей
- •Реакция цепи на экспоненциальное воздействие
- •Понятие об операторных характеристиках
- •Методы определения операторных характеристик
- •Дифференцирующие и интегрирующие цепи
- •Вопросы для самопроверки
- •Единичные функции и их свойства
- •Переходная и импульсная характеристики линейных цепей
- •Методы определения временных характеристик
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Определение реакции цепи на произвольное внешнее воздействие
- •Определение реакции цепи на произвольное внешнее воздействие по ее переходной характеристике
- •Определение реакции цепи на произвольное внешнее воздействие по ее импульсной характеристике
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 7. Основы теории четырехполюсников и многополюсников
- •Модуль 7.1. Многополюсники и цепи с многополюсными элементами
- •Задача анализа цепей с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Классификация проходных четырехполюсников
- •Основные уравнения и первичные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров неавтономных проходных четырехполюсников
- •Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.4. Невзаимные проходные четырехполюсники
- •Идеальные усилители напряжения и тока
- •Однонаправленные цепи и цепи с обратной связью
- •Идеальные операционные усилители
- •Преобразователи сопротивления
- •Вопросы для самопроверки
- •Задачи
- •Модуль 7.5. Электрические фильтры
- •Классификация электрических фильтров
- •Реактивные фильтры
- •Активные фильтры
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 8. Цепи с распределенными параметрами
- •Модуль 8.1. Задача анализа цепей с распределенными параметрами
- •Общие сведения
- •Общее решение дифференциальных уравнений длинной линии
- •Вопросы для самопроверки
- •Волновые процессы в однородной длинной линии
- •Режим стоячих волн
- •Режим смешанных волн
- •Вопросы для самопроверки
- •Задачи
- •Проходной четырехполюсник с распределенными параметрами
- •Входное сопротивление отрезка однородной длинной линии
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Распределение напряжения и тока в однородной линии без потерь при произвольном внешнем воздействии
- •Вопросы для самопроверки
- •Задачи
- •Модуль 8.5. Цепи с распределенными параметрами специальных типов
- •Резистивные линии
- •Неоднородные линии
- •Вопросы для самопроверки
- •Задачи
- •Ответы
- •Книга 9. Синтез электрических цепей
- •Модуль 9.1. Задача синтеза линейных электрических цепей
- •Понятие физической реализуемости
- •Основные этапы синтеза цепей
- •Вопросы для самопроверки
- •Понятие о положительных вещественных функциях
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.3. Методы реализации реактивных двухполюсников
- •Методы выделения простейших составляющих (метод Фостера)
- •Метод разложения в цепную дробь (метод Кауэра)
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 9.4. Основы синтеза линейных пассивных четырехполюсников
- •Задача синтеза четырехполюсников
- •Методы реализации пассивных четырехполюсников
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Ответы
- •Книга 10. Методы автоматизированного анализа цепей
- •Модуль 10.1. Задача автоматизированного анализа цепей
- •Понятие о ручных и машинных методах анализа цепей
- •Общие представления о программах машинного анализа цепей
- •Вопросы для самопроверки
- •Топологические матрицы и топологические уравнения
- •Свойства топологических матриц
- •Компонентные матрицы и компонентные уравнения
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Методы узловых напряжений и контурных токов
- •Метод переменных состояния
- •Формирование уравнений состояния в матричной форме
- •Вопросы для самопроверки
- •Задачи
- •Решения и методические указания
- •Модуль 10.4. Особенности современных программ автоматизированного анализа цепей
- •Выбор методов формирования уравнений электрического равновесия. Понятие о поколениях программ автоматизированного анализа цепей
- •Вопросы для самопроверки
- •Ответы
- •Заключение
- •Приложения
- •Приложение 1. Таблица оригиналов и изображений по Лапласу
- •Приложение 2. Основные уравнения проходных четырёхполюсников
- •Приложение 3. Соотношения между первичными параметрами проходных четырехполюсников
- •Приложение 5. Соотношения между первичными параметрами взаимных и симметричных четырехполюсников
- •Приложение 6. Приставки для образования кратных и дольных единиц
- •Приложение 7. Инструкция для работы с Самоучителем по курсу «Основы теории цепей»
- •Список литературы
Модуль 9.4. Основы синтеза линейных пассивных четырехполюсников
Цель модуля: ознакомление студентов с постановкой задачи синтеза пассив ных четырехполюсников и с простейшими методами синтеза четырехполюсников.
Задача синтеза четырехполюсников
Синтез четырехполюсников, как и синтез двухполюсников, можно производить во временной и частотной областях. Рассмотрим методы синтеза в частотной облас ти (т. е. по заданным операторным входным и передаточным характеристикам), от метив, что, поскольку проходной четырехполюсник может быть представлен раз личными входными и передаточными характеристиками, возможны разные вари анты постановки задачи синтеза, например, синтез четырехполюсника по заданным выражениям для первичных или вторичных параметров, по передаточной характе ристике в режиме холостого хода на выходе, по передаточной характеристике при согласованной, чисто резистивной или произвольной нагрузке.
Критерии физической реализуемости четырехполюсников формулируются различным образом в зависимости от постановки задачи синтеза и заданного или выбранного элементного базиса. В общем случае на вид операторных передаточных характеристик линейной пассивной цепи / накладывается мень ше ограничений, чем на вид операторных входных характеристик. В частности, сте пени полиномов и могут отличаться больше, чем на единицу, веществен ная часть передаточных функций на мнимой оси может быть отрицательной, а нули передаточных функций могут располагаться как в левой, так и в правой полуплоско стях (полюсы передаточных характеристик совпадают с нулями операторного вход ного сопротивления или операторной входной проводимости и не могут распола гаться в правой полуплоскости).
Минимально фазовые и неминимально фазовые четырехполюсники
Рассмотрим два четырехполюсника А и Б, операторные коэффициенты переда чи которых по напряжению определяются выражениями
А
Б
⁄ |
; |
9.9 |
⁄ |
, |
9.10 |
где a, b — действительные положительные числа. Функции |
A |
и Б имеют |
||
одинаковые полюсы хA |
хБ |
, расположенные в левой полуплоскости, и рав |
||
ные по модулю нули | А| |
| Б| |
, причем нуль функции |
A |
лежит в левой |
(рис. 9.15, а), а нуль функции Б |
в правой (рис. 9.15, б) полуплоскости. |
|||
Заменяя в выражениях (9.9) и (9.10) комплексную частоту |
на |
, определяем |
||
комплексные коэффициенты передачи рассматриваемых четырехполюсников по напряжению
А
Б
⁄
⁄
АА
ББ
; 9.11
.9.12
834
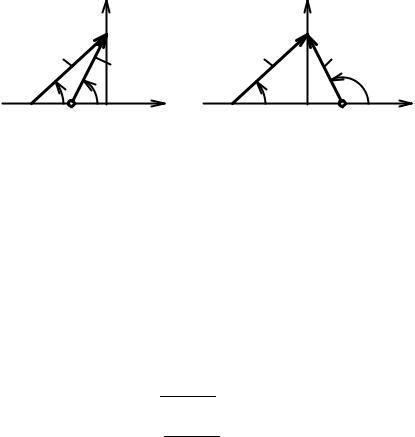
Рис. 9. 15. К понятиям минимально фазового и неминимально фазового четырехполюсни ков
Каждый из двучленов, стоящих в числителе и знаменателе этих выражений, можно изобразить на плоскости комплексного переменного в виде вектора, прове денного из нуля или полюса функций , Б в произвольную точку , лежа щую на мнимой оси (рис. 9.15). Следовательно, модули комплексных коэффициентов передачи четырехполюсников по напряжению равны отношению длин векторов, проведенных из нулей, к длинам векторов, проведенных из полюсов соответствую щих функций:
А
Б
|
|
; |
9.13 |
|
|
|
|
, |
9.14 |
а аргументы комплексных коэффициентов передачи четырехполюсников—разности углов, образуемых с положительным направлением вещественной оси векторами, проведенными из нулей, и векторами, проведенными из полюсов функции A и
Б.
А |
А |
А |
Б |
Б |
Б |
arctg |
⁄ |
arctg |
⁄ ; |
9.15 |
arctg |
⁄ |
arctg |
⁄ . |
9.16 |
Как следует из выражений (9.13) — (9.16), модули комплексных коэффициен тов передачи по напряжению обоих четырехполюсников равны, а аргумент ком плексного коэффициента передачи по напряжению четырехполюсника А меньше, чем соответствующий аргумент четырехполюсника Б. Таким образом, при одинако вых модулях аргумент передаточной функции, имеющей нули в правой полуплоско сти, больше аргумента передаточной функции, нули которой расположены только в левой полуплоскости. Полученный результат имеет весьма общий характер и рас пространяется на любые передаточные функции, имеющие произвольное число ну лей и полюсов, расположенных не только на вещественной оси, но и в произвольных точках плоскости .
В соответствии с указанным свойством четырехполюсники, передаточные функции которых не имеют нулей в правой полуплоскости, называются минималь
835
нофазовыми, а четырехполюсники, у которых хотя бы один нуль расположен в правой полуплоскости,— неминимальнофазовыми.
Комплексные частотные характеристики неминимально фазовых четырехпо люсников обладают рядом интересных особенностей. В частности, если у рассмот ренного неминимально фазового четырехполюсника Б параметры элементов вы браны таким образом, что
то |
модуль |
| Б| |
| хБ| |
, |
9.17 |
его коэффициента |
передачи |
по |
напряжению не зависит от |
||
ты: |
Б |
1, а аргумент коэффициента передачи по напряжению с изменением |
|||
частоты изменяется в пределах от |
до 0: Б |
|
2arctg ⁄ . |
||
Четырехполюсник с АЧХ и ФЧХ такого типа называется фазовым контуром, все пропускающим четырехполюсником или четырехполюсником чисто фазового сдви га. Фазовые контуры широко используют для коррекции ФЧХ цепей, т. е. когда необ ходимо изменять ФЧХ цепи без изменения ее АЧХ.
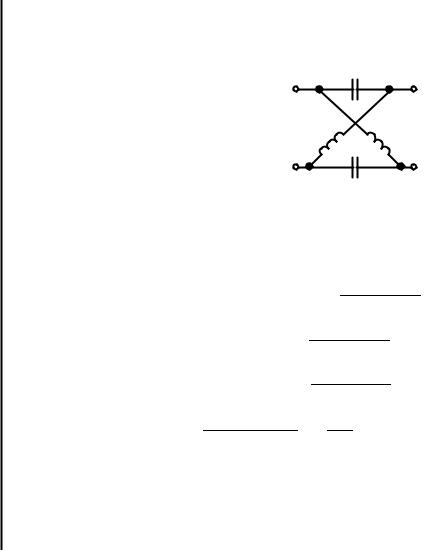
Пример9.10. Определим операторный коэффициент передачи по напряжению сим метричного мостового реактивного четырехполюсника рис. 9.16 при согласованной на грузке. Убедимся, что рассматриваемый четырехполюсник относится к фазовым контурам.
Рис. 9.16. К примеру 9.10
Используя выражения для первичных параметров симметричного мостового четы рехполюсника см. пример 7.16 , определяем A параметры рассматриваемой цепи:
|
|
|
|
|
|
|
|
1⁄ |
|
; |
|
|
|
|
|
|
|
|
|
2 |
|
|
1⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
⁄ |
; |
|
|
|
|
|
||
|
|
|
|
|
|
1⁄ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1⁄ |
|
|
|
|
|
||
Характеристическое сопротивление такого четырехполюсника имеет чисто рези |
||||||||||||||
стивный характер: |
⁄ |
⁄ |
, а операторный коэффициент передачи |
|||||||||||
по напряжению при согласованной нагрузке |
|
|
|
|
|
1⁄√ |
|
1⁄√ |
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
удовлетворяют условию |
|
||||||||||||
|
|
|
|
|||||||||||
Полюсы и нули |
9.17 , поэтому рассматриваемый |
|||||||||||||
четырехполюсник относится к фазовым контурам.
Существенное различие между минимально фазовыми и неминимально фазовыми четырехполюсниками заключается в том, что модуль и аргумент, равно
836

как и вещественная и мнимая части передаточной функции минимально фазового четырехполюсника связаны однозначными зависимостями, которые отсутствуют у неминимально фазовых четырехполюсников.
Методы реализации пассивных четырехполюсников
Задача синтеза четырехполюсников решается в два этапа: на первом этапе про веряют условия физической реализуемости заданных характеристик, на втором оп ределяют схему искомой цепи и параметры входящих в нее элементов (как и ранее, предполагаем, что искомые характеристики цепи заданы в виде аналитических вы ражений). Оставляя открытым вопрос о физической реализуемости операторных передаточных характеристик, рассмотрим некоторые простые приемы, позволяю щие свести задачу реализации пассивных четырехполюсников к задаче реализации пассивных двухполюсников.
Если синтез пассивного четырехполюсника производится по заданным выра жениям для первичных или вторичных параметров, то эффективный способ реше ния задачи заключается в использовании П образной или Т образной канонической схемы замещения взаимного четырехполюсника (см. рис. 7.14, б, в). Операторные входные сопротивления или операторные входные проводимости пассивных двух полюсников, входящих в канонические схемы замещения, определяют с помощью соотношений (7.58), (7.59) по известным выражениям для Z или параметров. Та ким образом, задача синтеза пассивного четырехполюсника сводится к задаче син теза пассивных двухполюсников, входящих в канонические схемы замещения.
Пример9.11. Найдем одну из возможных реализаций четырехполюсника,
параметры которого определяются выражениями |
12·10 |
|
|
|
|
720·10 |
276·10 |
|
См; |
||
360·10 |
42·10 |
1 |
|
||
|
60·10 |
8·10 |
См; |
|
|
270·10 |
30·10 |
1 |
|
||
30·10 |
15·10 |
1 |
См. |
||
|
30·10 |
1 |
|
|
|
Выберем для реализации П образную схему замещения четырехполюсника см. рис. 7.14, в и, используя соотношения 7.59 , определим операторные входные проводимости входящих в нее двухполюсников:
Y
|
|
4·10 |
1 |
|
3·10 |
|
1⁄ 12·10 |
|
См; |
|
|
12·10 |
|
|
|
||||
· |
· |
· |
2·10 |
|
· |
· |
См; |
||
|
|
|
7·10 |
|
1 См. |
|
|
||
|
Как следует из полученных выражений, двухполюсник |
может быть реализо |
|||||
ван в виде последовательного соединения емкости |
4 пФ и индуктивности |
3 мкГн. |
|||||
Двухполюсник |
можно представить в виде параллельного соединения емкости |
|
|||||
2 |
пФ и последовательной LC цепи, состоящей из емкости |
6 пФ и индуктивности |
|||||
5 |
мкГн, а двухполюсник |
— в виде параллельного соединения сопротивления |
1 Ом |
||||
и емкости |
7 пФ рис. 9.17 . |
|
|
|
|
||
837
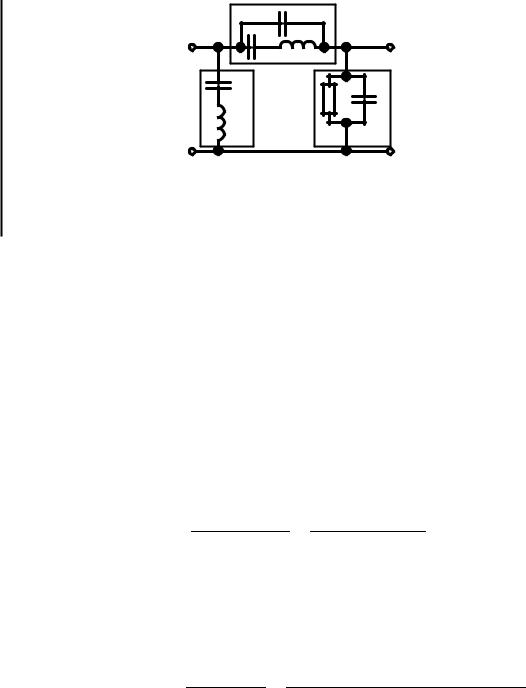
Рис. 9.17. К примеру 9.11
Синтезировать четырехполюсник по заданному операторному коэффициенту передачи по напряжению в режиме холостого хода ⁄ можно так же с использованием П или Т образных канонических схем замещения. Для этого необходимо так подобрать выражения для его или параметров, чтобы они обеспечивали заданную передаточную характеристику
х |
⁄ |
⁄ |
⁄ |
и были физически реализуемы. Заданный |
|
можно реализовать с помощью Г |
|
образного четырехполюсника с Т входом (см. рис. 7.17, а). Операторный коэффици ент передачи по напряжению такого четырехполюсника в режиме холостого хода определяется следующим выражением:
1 х 1 ⁄ . 9.18
Для нахождения операторных входных сопротивлений двухполюсников, обра зующих продольную и поперечную ветви Г образного четырехполюсника, приведем заданное выражение для коэффициента передачи к виду (9.18). Это достигается пу
тем деления полиномов |
и |
на некоторый полином |
: |
|
|
|
|
⁄ |
⁄ |
|
, |
х |
|
⁄ |
⁄ |
⁄ |
|
выбранный таким образом, чтобы функции |
⁄ |
|
|||
|
|
⁄ |
и |
|
|
были физически реализуемыми.
Следует иметь в виду, что нули операторного коэффициента передачи по на пряжению четырехполюсника, составленного по Г образной схеме, совпадают с ну лями сопротивления и полюсами сопротивления и, следовательно, нахо дятся в левой полуплоскости. Поэтому Г образную схему можно использовать толь ко для реализации операторных передаточных характеристик минимально фазовых четырехполюсников.
838
Пример9.12. Используя Г образную схему, построим четырехполюсник, оператор ный коэффициент передачи по напряжению которого в режиме холостого хода
10
х180 37 1.
Разделим числитель и знаменатель данного выражения на полином 30 2 , выбранный таким образом, чтобы операторные входные сопротивления
продольного и поперечного плеч Г образного четырехполюсника представляли собой положительные вещественные функции:
|
|
|
|
|
|
|
15 |
5 |
|
1 |
|
|
3 |
1 |
|
1⁄15 |
; |
|
|
||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
6 |
1 |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||
|
Как следует из полученных выражений, сопротивление |
|
|
может быть реализо |
|||||||||||||||||||||
вано в виде параллельного соединения емкости |
|
|
|
|
3 Ф и индуктивности |
5 Гн, а со |
|||||||||||||||||||
противление |
— в виде последовательного соединения индуктивности |
6 Гн и ем |
|||||||||||||||||||||||
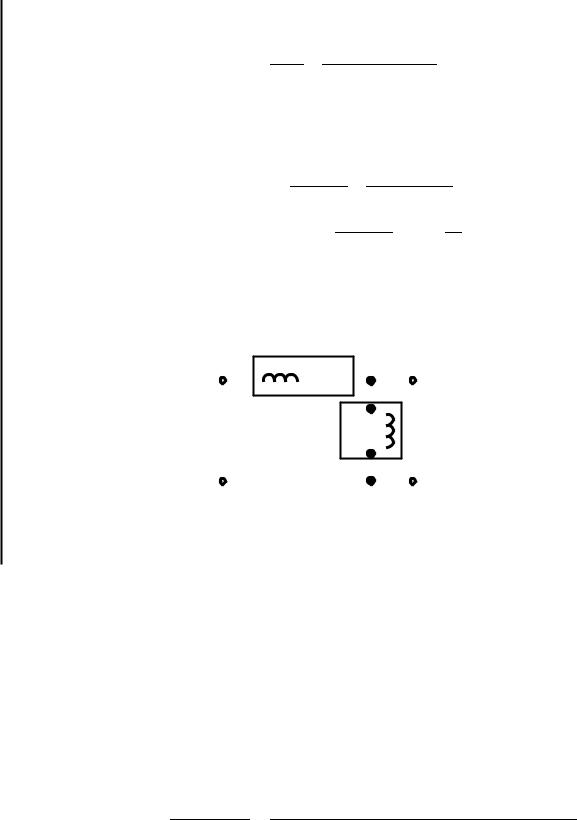
кости |
2 Ф |
рис. 9.18 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.18. К примеру 9.12
Четырехполюсник с заданным операторным коэффициентом передачи по на
пряжению в режиме холостого хода |
можно реализовать и по симметричной |
|
мостовой схеме (см. рис. 7.18, а), причем в этом случае нули |
могут распола |
|
гаться как в левой, так и в правой полуплоскости. Коэффициент передачи по напря жению полученного четырехполюсника может быть выражен через сопротивления
продольных |
и скрещивающихся |
|
ветвей (см. пример 7.14): |
. |
9.19 |
|||||
|
х |
|
⁄ |
|
⁄ |
|||||
Разделим числитель и знаменатель заданного выражения для |
|
на неко |
||||||||
торый полином |
|
и преобразуем полученное выражение к виду (9.19): |
|
|
||||||
|
|
|
⁄ |
|
⁄ |
⁄ |
|
. 9.20 |
||
х |
|
|
⁄ |
|
|
|
⁄ |
⁄ |
|
|
Из сравнения выражений (9.19) и (9.20) видно, что если полином |
|
выбран |
||||||||
таким образом, что операторные сопротивления |
|
9.21 |
||||||||
|
|
|
|
⁄ |
; |
⁄ |
|
|||
839
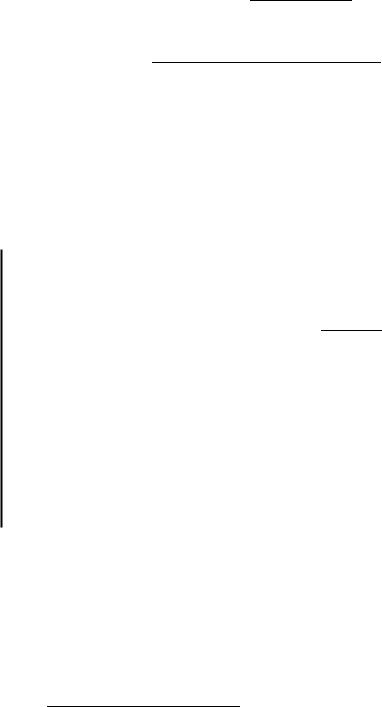
могут быть физически реализованы, то симметричный мостовой четырехполюсник, сопротивления продольных и скрещивающихся ветвей которого определяются вы ражениями (9.21), будет обладать заданным операторным коэффициентом передачи по напряжению.
Симметричный мостовой четырехполюсник можно использовать и для реали зации заданного операторного коэффициента передачи по напряжению в режиме согласованной нагрузки. В этом случае и могут быть определены с по мощью выражений (7.82), (7.86)*:
|
|
|
1 |
⁄ |
|
|
|
|
|
; |
|
. |
9.22 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Используя (9.22), выразим сопротивления продольных и скрещивающихся вет |
|||||||||||||
вей четырехполюсника через сопротивление нагрузки н |
|
|
и коэффициент |
||||||||||
передачи по напряжению |
: |
|
|
|
|
|
|
|
|
|
|
|
|
1
1
н
н
⁄ 1 |
; |
9.23 |
⁄ 1 |
. |
Пример9 13. Построим четырехполюсник, операторный коэффициент передачи по напряжению которого при согласованной нагрузке н 10 Ом определяется выражени ем
|
|
10 |
. |
|
Подставляя заданные значения |
и н |
10 |
9.23 , определяем опера |
|
в выражения |
||||
торные сопротивления продольных |
и скрещивающихся |
ветвей симметричного |
||
мостового четырехполюсника: |
10·10 |
Ом; |
|
|
|
1⁄ 0,1·10 |
|
Ом. |
|
Таким образом, заданный коэффициент передачи |
может быть реализован с помо |
|
щью реактивного мостового четырехполюсника рис. 9.19 |
, содержащего индуктивности |
|
10 мкГн в продольных и емкости |
0,1 мкФ в скрещивающихся ветвях. |
|
* Выражения для А параметров симметричного мостового четырехполюсника приведены в примере 7.16.
840
