
- •Оглавление
- •Введение
- •Глава 1. Основные показатели макроэкономики
- •1.1. Общественное воспроизводство
- •1.2. Национальное богатство
- •1.3. Система национального счетоводства
- •1.4. Связь между основными показателями макроэкономики
- •1.5. Методы расчета ВВП
- •1.6. Личный и располагаемый доходы
- •1.7. Качество и уровень жизни
- •1.8. Конечное потребление
- •1.9. Коэффициент концентрации Джини
- •1.10. Отраслевая структура национальной экономики
- •1.11. Межотраслевой баланс
- •1.12. Статический межотраслевой баланс
- •1.13. Цены в статической системе межотраслевых связей
- •Упражнения
- •Библиографический список
- •Глава 2. Модели межотраслевого баланса
- •2.1. Схема межотраслевого баланса
- •2.2. Коэффициенты полных материальных затрат
- •2.3. Продуктивная матрица
- •2.4. Динамическая модель межотраслевого баланса
- •2.5. Модель Неймана
- •Упражнения
- •Библиографический список
- •Глава 3. Макроэкономические производственные функции
- •3.1. Понятие макроэкономической производственной функции
- •3.2. Свойства макроэкономической производственной функции
- •3.3. Мультипликативная макроэкономическая производственная функция
- •3.4. Построение производственной функции
- •3.5. Основные характеристики макроэкономической производственной функции
- •3.6. Изокванты и изоклинали
- •3.7. Эффективность и масштаб производства
- •Упражнения
- •Библиографический список
- •Глава 4. Модели потребления
- •4.1. Кейнсианская модель потребления
- •4.2. Модель Фишера
- •4.3. Модель Модильяни
- •4.4. Модель Фридмена
- •4.5. Функция полезности
- •4.6. Линии безразличия
- •4.7. Оптимизация функции полезности
- •4.8. Задача потребительского выбора для произвольного числа товаров
- •4.9. Уравнение Слуцкого
- •4.10. Кривые «доход-потребление»
- •4.11. Кривые «цена-потребление»
- •4.12. Макроэкономические инвестиции
- •4.13. Характеристики инвестиций
- •4.14. Спрос на инвестиции
- •Упражнения
- •Библиографический список
- •Глава 5. Теории экономического роста
- •5.1. Факторы экономического роста
- •5.2. Модель Харрода—Домара
- •5.3. Модель Солоу
- •5.4. «Золотое правило» накопления
- •Упражнения
- •Библиографический список
- •Глава 6. Макроэкономическое равновесие на товарном рынке
- •6.1. Понятие макроэкономического равновесия
- •6.2. Классическая модель макроэкономического равновесия
- •6.3. Модель совокупного спроса
- •6.4. Модель совокупного предложения
- •6.6. Модель «кейнсианский крест»
- •6.7. Мультипликатор автономных расходов
- •6.8. Парадокс бережливости
- •Упражнения
- •Библиографический список
- •Глава 7. Макроэкономическое равновесие на денежном рынке
- •7.1. Сущность и функции денег
- •7.2. Денежная масса
- •7.3. Модель инфляции
- •7.4. Теории спроса на деньги
- •7.4.1. Классическая теория спроса на деньги
- •7.4.3. Кейнсианская теория спроса на деньги
- •7.4.4. Монетаристская теория спроса на деньги
- •7.5. Предложение денег
- •7.6. Равновесие на рынке денег
- •Упражнения
- •Библиографический список
- •Глава 8. Макроэкономическое равновесие на товарном и денежном рынках
- •8.1. Линия инвестиции-сбережения (IS)
- •8.2. Линия предпочтение ликвидности-деньги (LM)
- •8.3. Модель IS—LM
- •8.4. Динамика установления макроэкономического равновесия на совместном рынке
- •8.7. Ликвидная ловушка
- •8.8. Модель совокупного спроса
- •Упражнения
- •Библиографический список
- •Глава 9. Экономические циклы
- •9.1. Понятие экономических циклов
- •9.2. Мировые циклы Кондратьева
- •9.3. Технологические уклады
- •9.4. Особенности циклического развития различных стран
- •9.5. Среднесрочные циклы
- •9.6. Теории экономических циклов
- •9.6.1. Модель Самуэльсона—Хикса
- •9.6.2. Модель Тевеса
- •9.6.3. Модель Гудвина
- •9.7. Практическое использование экономических циклов
- •9.7.1. Прогнозирование
- •9.7.2. Модель Ханса Виссема
- •Упражнения
- •Библиографический список
- •Глава 10. Рынок труда
- •10.1. Понятие рынка труда и рабочей силы
- •10.2. Спрос на труд
- •10.3. Предложение труда
- •10.4. Равновесие на рынке труда и безработица
- •10.5. Безработица и ее характеристики
- •10.6. Модель Оукена
- •10.7. Инфляция и ее виды
- •10.8. Адаптивные и рациональные ожидания
- •10.9. Инфляция и безработица — кривая Филлипса
- •10.10. Антиинфляционная политика
- •Упражнения
- •Библиографический список
- •Глава 11. Рынок ценных бумаг и его инструменты
- •11.1. Понятие рынка ценных бумаг
- •11.2. Анализ характеристик ценных бумаг
- •11.2.1. Технический анализ
- •11.2.2. Фундаментальный анализ
- •11.3. Риск и ограничение риска
- •11.3.1. Хеджирование
- •11.3.2. Мера риска
- •11.4. Индексы деловой активности
- •11.5. Основные характеристики акций
- •11.6. Основные характеристики облигаций
- •11.7. Государственные облигации
- •11.8. Дюрация и изгиб
- •11.9. Форвардные контракты
- •11.10. Паритет покупательной способности
- •11.11. ФЬЮЧЕРСНЫЕ КОНТРАКТЫ
- •11.12. Опционы
- •Упражнения
- •Библиографический список
- •Глава 12. Портфель ценных бумаг
- •12.1. Характеристики портфеля ценных бумаг
- •12.2. Портфель из двух типов ценных бумаг
- •12.3. Оптимальный портфель
- •12.4. Определение состава оптимального портфеля
- •12.5. Определение состава оптимального портфеля в Excel
- •12.6. Оптимальный портфель с добавлением безрисковых ценных бумаг
- •12.7. Алгоритм построения оптимального портфеля ценных бумаг
- •12.8. Рыночный портфель
- •12.9. Эффективный рынок ценных бумаг
- •Упражнения
- •Библиографический список
- •13.1. Фискальная политика государства
- •13.2. Налоговые органы Российской Федерации
- •13.3. Ответственность за налоговые правонарушения в Российской Федерации
- •13.4. Виды налогов
- •13.5. Суммарная выплата по основным налогам
- •13.7. Оптимизация налоговой ставки. Кривая Лаффера
- •13.8. Модель государственного бюджета
- •13.9. Доходы и расходы государственного бюджета
- •13.10. Бюджетный дефицит
- •Упражнения
- •Библиографический список
- •Ответы и решения
- •Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Глава 5
- •Глава 6
- •Глава 7
- •Глава 8
- •Глава 9
- •Глава 10
- •Глава 11
- •Глава 12
- •Глава 13

Ответы и решения |
447 |
При покупке спрэда бабочки прибыли-убытки инвестора в рас- |
|
чете на 1000 евро составят: |
|
П a с 2b 1000 0, 3 0, 2 2 0, 4 1000 300 |
ðóá. |
При продаже спрэда бабочки прибыль инвестора в расчете на 1000 евро составит:
П a c 2b 1000 0,3 0, 2 2 0, 4 1000 300 ðóá.
Рассчитанные двумя методами результаты совпали.
Глава 12
Задача 12.1. Состав портфеля в оптимальной точке:
|
|
|
|
2 |
|
|
0, 9 0, 2 |
|
||
x |
0 |
|
|
2 |
|
12 |
|
|
0, 6364. |
|
2 |
2 |
2 |
0, 6 0,9 2 0, 2 |
|||||||
|
|
|
|
|||||||
|
|
|
1 |
|
2 |
12 |
|
|
|
|
Доходность портфеля и риск в оптимальной точке:
ap,0 x0a1 1 x0 a2 0, 6364 0,12 1 0, 6364 0, 2 0,1491;
|
p,0 |
x02 12 1 x0 2 22 2x0 1 x0 12 |
|
0, 63642 0, 6 (1 0, 6364)2 0,9 2 0, 6364 (1 0, 6364) 0, 2 0, 674. |
|
Доходность портфеля и риск в крайних точках и в оптимальной точке представлены в табл. ОР.3.
|
|
|
Таблица ОР.3 |
x |
|
|
|
1 |
0,6364 |
0 |
|
ap |
0,12 |
0,1491 |
0,2 |
p |
0,745 |
0,674 |
0,949 |
График доходность-риск портфеля представлен на рис. ОР.6.
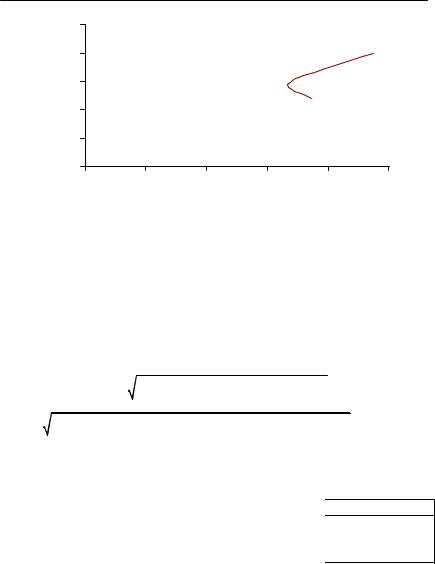
448
Доходность
Ðèñ. ÎÐ.6. График зависимости ожидаемой доходности
оптимального портфеля от его риска
Задача 12.2. Состав портфеля в оптимальной точке:
|
|
|
|
2 |
|
|
1, 2 0,3 |
|
|||
x |
0 |
|
|
2 |
|
12 |
|
|
|
0, 643. |
|
2 |
2 |
2 |
0,8 1, 2 2 0,3 |
||||||||
|
|
|
|
||||||||
|
|
|
1 |
|
2 |
12 |
|
|
|
|
|
Доходность портфеля и риск в оптимальной точке:
ap,0 x0a1 1 x0 a2 0, 643 0,15 1 0, 643 0,3 0, 204;
|
p,0 |
x02 12 1 x0 2 22 2x0 1 x0 12 |
|
0, 6432 0,8 (1 0, 643)2 1, 2 2 0, 643 1 0, 643 0, 3 0,588. |
|
Доходность портфеля и риск в крайних точках и в оптимальной точке представлены в табл. ОР.4.
|
|
|
Таблица ОР.4 |
|
|
|
|
x |
1 |
0,643 |
0 |
ap |
0,15 |
0,204 |
0,3 |
p |
0,894 |
0,788 |
1,095 |
График доходность-риск портфеля представлен на рис. ОР.7.

Ответы и решения |
449 |
Доходность
0,35
0,30
0,25
0,20
0,15
0,10
0,05
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
Стандартное отклонение
Ðèñ. ÎÐ.7. График зависимости ожидаемой
доходности портфеля от риска
Задача 12.3. Для определения состава оптимального портфеля в экстремальной точке найдем обратную матрицу 1 матрицы риска
1 |
0 |
0 |
1 |
|
0 1, 6 |
0 |
1 |
|
|
|
0 |
2,8 1 |
. |
|
0 |
|
|||
1 |
1 |
1 |
0 |
|
Для расчета элементов обратной матрицы использованы программы Excel. Для этих целей:
1)вносят значения элементов матрицы в таблицу;
2)выделяют поле для записи обратной матрицы;
3)нажимают на кнопку « fx »;
4)в категориях «Математические» выбирают функцию «МОБР»;
5)ÎÊ;
6)выделяют преобразуемую матрицу;
7)одновременно нажимают кнопки Ctrl+Shift+Enter.
Обратная матрица равна:
|
|
|
0, |
495495 |
0, |
315315 |
0,180180 |
0, 504505 |
|
|
1 |
|
0, |
315315 |
0, |
427928 |
0,112613 |
0,315315 |
|
|
|
0,180180 |
0,112613 |
0, 292793 |
0,180180 |
. |
|||
|
|
|
|
||||||
|
|
|
0,504505 |
0,315315 |
0,180180 |
0, 504505 |
|||

450
Далее находим матрицу-столбец состава портфеля:
|
0, |
495495 |
0, |
315315 |
0,180180 |
0, 504505 |
0 |
|
0,504505 |
||
|
0, |
315315 |
0, |
427928 |
0,112613 |
0, |
315315 |
0 |
|
0, |
315315 |
|
0,180180 |
0,112613 |
0, 292793 |
|
|
|
|
|
. |
||
|
0,180180 |
0 |
|
0,180180 |
|||||||
|
0, 504505 |
0,315315 |
0,180180 |
0, |
504505 |
1 |
|
0, |
504505 |
||
Доли ценных бумаг первого x1 , второго x2 и третьего x3
типов представлены соответственно в первой, второй и третьей строках матрицы-столбца состава портфеля.
Найдем доходность портфеля в этой точке и риск: |
|
|
|||||||||
|
|
|
|
|
0, 5045 |
|
|
|
|
||
|
|
|
|
0, 3153 |
|
0,1355; |
|
|
|||
ap a x 0, 09 0,16 0, 22 |
|
|
|
|
|||||||
|
|
|
|
0,1802 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
2p x x 0,5045 |
0, 3153 0,1802 |
1 |
0 |
0 |
0, 5045 |
|
|
||||
|
0 |
1, 6 |
0 |
|
|
0, 3153 |
|
0,504505; |
|||
|
|
|
0 |
0 |
|
|
|
0,1802 |
|
|
|
|
|
|
2,8 |
|
|
|
|||||
р 0, 71.
Состав, доходность и риск портфеля в экстремальной точке записаны в табл. ОР.5.
Для определения состава оптимального портфеля найдем обратную матрицу А 1 матрицы риск-доходность:
|
1 |
0 |
0 |
0, 09 1 |
|
|
|
0 |
1, 6 |
0 |
0,16 |
1 |
|
А |
0 |
0 |
2, 4 0, 22 1 |
. |
||
|
|
0,16 0, 22 |
0 |
|
|
|
0, 09 |
0 |
|||||
|
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
Обратная матрица равна: |
|
|
|
||
|
0, 081154 |
0,175834 |
0, 094680 |
9,107304 |
1, 738503 |
|
0,175834 |
0, 380974 |
0, 205140 |
3, 065825 0,100090 |
|
А 1 |
0, 094680 |
0, 205140 |
0,110460 |
6, 041479 |
0, 638413 . |
|
9,107304 |
3, 065825 |
6, 041479 |
200,180300 |
|
|
27,123530 |
||||
|
1, 738503 |
0,100090 |
0, 638413 |
27,123530 |
4,179621 |
|
|
|
|
|
|
Ответы и решения |
|
|
|
|
|
|
451 |
|
||||
Далее находим матрицу-столбец состава портфеля для доходно- |
||||||||||||
сти портфеля 0,15: |
|
|
|
|
|
|
|
|
|
|||
|
|
0, 081154 |
0,175834 |
0, 094680 |
9,107304 |
1, 738503 |
|
|
0 |
|
|
|
|
|
0,175834 |
0,380974 |
0, 205140 |
3, 065825 |
0,100090 |
|
|
0 |
|
|
|
X |
|
0, 094680 |
0, 205140 |
0,110460 |
6, 041479 |
|
|
|
0 |
|
|
|
|
0, 638413 |
|
|
|||||||||
|
|
9,107304 |
3, 065825 |
6, 041479 |
200,180300 |
27,123530 |
|
0,15 |
|
|
||
|
|
1, 738503 |
0,100090 |
0, 638413 |
27,123530 |
4,179621 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3724 |
|
|
|
0,3598 |
|
|
|
0, 2678 |
|
|
. |
||
|
|
2, 9035 |
|
|
|
0,1111 |
|
|
|
|
|
Доли ценных бумаг первого x1 , второго x2 и третьего x3
типов представлены соответственно в первой, второй и третьей строках матрицы-столбца состава портфеля.
Риск портфеля в этой точке определяется по формуле |
|
|||||||||||||
2p x x 0,3724 0,3598 |
|
1 |
0 |
0 |
0, 3724 |
|
|
|||||||
0, 2678 |
0 1, 6 |
0 |
|
|
0,3598 |
0, 54662; |
||||||||
|
|
|
|
|
|
0 |
0 |
2,8 |
|
|
0, 2678 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
р 0, 739. |
|
|
|
|
|
|
|
|
|
|
Аналогичным образом находят состав и риск для других доход- |
||||||||||||||
ностей, которые представлены в табл. ОР.5. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица ОР.5 |
||
|
|
|
|
|
|
|
|
|
|
|||||
ap |
0,1057 |
0,12 |
0,13 |
0,1355 |
|
0,15 |
|
0,17 |
0,1909 |
|||||
x1 |
0,7758 |
0,6456 |
0,5545 |
0,5045 |
|
0,3724 |
0,1903 |
0 |
||||||
x2 |
0,224 |
0,2676 |
0,2985 |
0,3153 |
|
0,3598 |
0,4211 |
0,4851 |
||||||
x3 |
0,0002 |
0,0866 |
0,147 |
0,1802 |
|
0,2678 |
0,3886 |
0,5149 |
||||||
p |
0,826 |
0,74 |
0,715 |
0,71 |
|
0,739 |
0,862 |
1,059 |
||||||
График доходность-риск, построенный по данным табл. ОР.5, представлен на рис. ОР.8.

452
Доходность
Ðèñ. ÎÐ.8. Доходность-риск оптимального портфеля
Задача 12.4. Состав портфеля для рисковых ценных бумаг первого, второго и третьего типов определен при решении задачи 12.3. Построен также график доходность-риск, представленный на рис. ОР.9 в виде кривой линии.
|
0,25 |
|
|
|
|
|
|
Доходность |
0,20 |
|
|
|
|
|
|
0,15 |
|
|
|
|
|
|
|
0,10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
–0,2 |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
|
|
|
Стандартное отклонение |
|
|
|
|
Ðèñ. ÎÐ.9. Доходность-риск оптимального портфеля
Функция ожидаемой доходности портфеля от среднего квадратичного отклонения имеет вид:
aр aр,k a0 р a0 ,
р,k
ãäå р,k , aр,k — координаты точки касания прямой линии и функции доходность-риск для рисковых ценных бумаг портфеля.
Ответы и решения |
453 |
В точке касания безрисковые ценные бумаги отсутствуют, т.е. х0 0 . Доходность портфеля в точке касания можно найти из уравнения (12.20). Запишем это уравнение в виде:
x0 |
|
|
|
0 |
|
||
x |
|
|
|
0 |
|
|
|
|
1 |
|
А 1 |
|
|
|
|
|
х2 |
|
... |
, ãäå |
|||
x3 |
|
|
|
0 |
|
||
|
|
|
|
ap |
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
0 |
0 |
0 |
0 |
0, 06 1 |
|
|
|
|
0 |
1 |
0 |
0 |
0, 09 1 |
|
|
|
|
0 |
0 |
1, 6 |
0 |
0,16 |
1 |
|
A |
|
|
||||||
|
0 |
0 |
0 |
2,8 |
0, 22 1 |
. |
||
|
0, 06 |
0, 09 0,16 0, 22 |
0 |
0 |
||||
|
|
1 |
1 |
1 |
1 |
0 |
|
|
|
|
0 |
||||||
При значении доходности ap,k 0,16887828 имеем следующий состав оптимального портфеля:
х0 0; |
x1 0, 2005; |
x2 0, 4176; |
x3 0,3819. |
Дисперсию портфеля в точке касания найдем по первой формуле (12.23) для оптимального портфеля, состоящего из рисковых бумаг:
|
1 |
0 |
0 |
|
0, |
2005 |
|
|
||
2p x x 0, 2005 0, 4176 |
0,3819 |
0 |
1, 6 |
0 |
|
|
0, |
4176 |
|
0, 7276. |
|
|
0 |
0 |
2,8 |
|
|
0,3819 |
|
|
|
|
|
|
|
|
|
|||||
Риск в точке касания равен:
p,k 0,853.
Таким образом, функция ожидаемой доходности портфеля от среднего квадратичного отклонения приобретает вид:
aр 0,16887828 0, 06 р 0, 06 0,128 р 0, 06. 0,853
График этой прямой показан на приведенном выше рис. ОР.9. Так как инвестор выбрал для своего портфеля среднюю до-
ходность 0,14, то доля бумаг в портфеле находится по формуле
(12.20):
