
- •Оглавление
- •Введение
- •Глава 1. Основные показатели макроэкономики
- •1.1. Общественное воспроизводство
- •1.2. Национальное богатство
- •1.3. Система национального счетоводства
- •1.4. Связь между основными показателями макроэкономики
- •1.5. Методы расчета ВВП
- •1.6. Личный и располагаемый доходы
- •1.7. Качество и уровень жизни
- •1.8. Конечное потребление
- •1.9. Коэффициент концентрации Джини
- •1.10. Отраслевая структура национальной экономики
- •1.11. Межотраслевой баланс
- •1.12. Статический межотраслевой баланс
- •1.13. Цены в статической системе межотраслевых связей
- •Упражнения
- •Библиографический список
- •Глава 2. Модели межотраслевого баланса
- •2.1. Схема межотраслевого баланса
- •2.2. Коэффициенты полных материальных затрат
- •2.3. Продуктивная матрица
- •2.4. Динамическая модель межотраслевого баланса
- •2.5. Модель Неймана
- •Упражнения
- •Библиографический список
- •Глава 3. Макроэкономические производственные функции
- •3.1. Понятие макроэкономической производственной функции
- •3.2. Свойства макроэкономической производственной функции
- •3.3. Мультипликативная макроэкономическая производственная функция
- •3.4. Построение производственной функции
- •3.5. Основные характеристики макроэкономической производственной функции
- •3.6. Изокванты и изоклинали
- •3.7. Эффективность и масштаб производства
- •Упражнения
- •Библиографический список
- •Глава 4. Модели потребления
- •4.1. Кейнсианская модель потребления
- •4.2. Модель Фишера
- •4.3. Модель Модильяни
- •4.4. Модель Фридмена
- •4.5. Функция полезности
- •4.6. Линии безразличия
- •4.7. Оптимизация функции полезности
- •4.8. Задача потребительского выбора для произвольного числа товаров
- •4.9. Уравнение Слуцкого
- •4.10. Кривые «доход-потребление»
- •4.11. Кривые «цена-потребление»
- •4.12. Макроэкономические инвестиции
- •4.13. Характеристики инвестиций
- •4.14. Спрос на инвестиции
- •Упражнения
- •Библиографический список
- •Глава 5. Теории экономического роста
- •5.1. Факторы экономического роста
- •5.2. Модель Харрода—Домара
- •5.3. Модель Солоу
- •5.4. «Золотое правило» накопления
- •Упражнения
- •Библиографический список
- •Глава 6. Макроэкономическое равновесие на товарном рынке
- •6.1. Понятие макроэкономического равновесия
- •6.2. Классическая модель макроэкономического равновесия
- •6.3. Модель совокупного спроса
- •6.4. Модель совокупного предложения
- •6.6. Модель «кейнсианский крест»
- •6.7. Мультипликатор автономных расходов
- •6.8. Парадокс бережливости
- •Упражнения
- •Библиографический список
- •Глава 7. Макроэкономическое равновесие на денежном рынке
- •7.1. Сущность и функции денег
- •7.2. Денежная масса
- •7.3. Модель инфляции
- •7.4. Теории спроса на деньги
- •7.4.1. Классическая теория спроса на деньги
- •7.4.3. Кейнсианская теория спроса на деньги
- •7.4.4. Монетаристская теория спроса на деньги
- •7.5. Предложение денег
- •7.6. Равновесие на рынке денег
- •Упражнения
- •Библиографический список
- •Глава 8. Макроэкономическое равновесие на товарном и денежном рынках
- •8.1. Линия инвестиции-сбережения (IS)
- •8.2. Линия предпочтение ликвидности-деньги (LM)
- •8.3. Модель IS—LM
- •8.4. Динамика установления макроэкономического равновесия на совместном рынке
- •8.7. Ликвидная ловушка
- •8.8. Модель совокупного спроса
- •Упражнения
- •Библиографический список
- •Глава 9. Экономические циклы
- •9.1. Понятие экономических циклов
- •9.2. Мировые циклы Кондратьева
- •9.3. Технологические уклады
- •9.4. Особенности циклического развития различных стран
- •9.5. Среднесрочные циклы
- •9.6. Теории экономических циклов
- •9.6.1. Модель Самуэльсона—Хикса
- •9.6.2. Модель Тевеса
- •9.6.3. Модель Гудвина
- •9.7. Практическое использование экономических циклов
- •9.7.1. Прогнозирование
- •9.7.2. Модель Ханса Виссема
- •Упражнения
- •Библиографический список
- •Глава 10. Рынок труда
- •10.1. Понятие рынка труда и рабочей силы
- •10.2. Спрос на труд
- •10.3. Предложение труда
- •10.4. Равновесие на рынке труда и безработица
- •10.5. Безработица и ее характеристики
- •10.6. Модель Оукена
- •10.7. Инфляция и ее виды
- •10.8. Адаптивные и рациональные ожидания
- •10.9. Инфляция и безработица — кривая Филлипса
- •10.10. Антиинфляционная политика
- •Упражнения
- •Библиографический список
- •Глава 11. Рынок ценных бумаг и его инструменты
- •11.1. Понятие рынка ценных бумаг
- •11.2. Анализ характеристик ценных бумаг
- •11.2.1. Технический анализ
- •11.2.2. Фундаментальный анализ
- •11.3. Риск и ограничение риска
- •11.3.1. Хеджирование
- •11.3.2. Мера риска
- •11.4. Индексы деловой активности
- •11.5. Основные характеристики акций
- •11.6. Основные характеристики облигаций
- •11.7. Государственные облигации
- •11.8. Дюрация и изгиб
- •11.9. Форвардные контракты
- •11.10. Паритет покупательной способности
- •11.11. ФЬЮЧЕРСНЫЕ КОНТРАКТЫ
- •11.12. Опционы
- •Упражнения
- •Библиографический список
- •Глава 12. Портфель ценных бумаг
- •12.1. Характеристики портфеля ценных бумаг
- •12.2. Портфель из двух типов ценных бумаг
- •12.3. Оптимальный портфель
- •12.4. Определение состава оптимального портфеля
- •12.5. Определение состава оптимального портфеля в Excel
- •12.6. Оптимальный портфель с добавлением безрисковых ценных бумаг
- •12.7. Алгоритм построения оптимального портфеля ценных бумаг
- •12.8. Рыночный портфель
- •12.9. Эффективный рынок ценных бумаг
- •Упражнения
- •Библиографический список
- •13.1. Фискальная политика государства
- •13.2. Налоговые органы Российской Федерации
- •13.3. Ответственность за налоговые правонарушения в Российской Федерации
- •13.4. Виды налогов
- •13.5. Суммарная выплата по основным налогам
- •13.7. Оптимизация налоговой ставки. Кривая Лаффера
- •13.8. Модель государственного бюджета
- •13.9. Доходы и расходы государственного бюджета
- •13.10. Бюджетный дефицит
- •Упражнения
- •Библиографический список
- •Ответы и решения
- •Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Глава 5
- •Глава 6
- •Глава 7
- •Глава 8
- •Глава 9
- •Глава 10
- •Глава 11
- •Глава 12
- •Глава 13

11. Рынок ценных бумаг и его инструменты |
327 |
Для облигаций с выплатой по купонам один раз в году уравнение для определения доходности запишем в виде:
K −u 1−(1+r )−n −(1+r)−n = 0. r
Курс бескупонной облигации, по которой в конце срока выпла- чивается только номинал, определяется из соотношения
K −(1+r )−n = 0 . Решив это уравнение относительно r, находим доходность бескупонной облигации:
r = n 1K −1.
Z Пример 11.11. Бескупонная облигация со сроком 7 лет куплена по курсу 79%.
Определить доходность инвестиций.
Р е ш е н и е. Доходность определяется по формуле r = 7 0,791 −1 = 0,034248, èëè ≈ 3, 42%. W
11.7. Государственные облигации
Государственные ценные бумаги являются финансовыми инструментами, обслуживающими государственный внутренний долг, и представляют собой облигации и векселя Министерства финансов РФ. Рынок государственных ценных бумаг служит для привлечения финансовых ресурсов, а для инвесторов является выгодным направлением вложения денежных средств.
Федеральными государственными ценными бумагами признаются бумаги, выпущенные от имени Российской Федерации. Денежные средства, привлекаемые в результате размещения государственных ценных бумаг, и порядок их расходования определяются законами Российской Федерации.
Эмитентом на рынке государственных ценных бумаг выступает государство в лице Министерства финансов РФ. Первичное размещение и погашение ценных бумаг осуществляется Центральным банком РФ по поручению Министерства финансов РФ.
Инвестором на рынке государственных ценных бумаг может быть любое юридическое или физическое лицо, резиденты и нерезиденты.
Контролирующим органом на рынке государственных ценных бумаг является Центральный банк РФ.
328 |
III. Фондовый рынок |
Существенную долю в структуре внутреннего государственного долга занимают государственные краткосрочные облигации (ГКО) и облигации федерального займа (ОФЗ). Полученные от реализации этих облигаций средства используются для покрытия дефицита федерального бюджета. Выпускаются бескупонные облигации и облигации с выплатами по купонам.
Облигации государственного сберегательного займа (ОГСЗ) предназначены для активного привлечения средств населения. ГКО
èОФЗ предназначены для физических и юридических лиц. Однако участие физических лиц в операциях с этими ценными бумагами весьма затруднительно. Это связано с тем, что операции куплипродажи этих облигаций проводятся только через биржевые торги, к участию в которых допущены уполномоченные дилеры. Дилер работает только с крупными суммами, которыми подавляющее большинство населения не обладает. Поэтому для частных лиц выпущены ОГСЗ с номинальной стоимостью 500 руб. Облигации выпускаются в документарной форме со сроком обращения 1—2 ãîäà
èрегулярной выплатой дохода по купонам. Купонный период составляет три месяца. Купонный доход определяется по аналогии с доходом по ОФЗ и привязан к среднему уровню доходности по ГКО. При этом обычно устанавливается премия к расчетному среднему уровню доходности. Реализация облигаций осуществляется через уполномоченные банки, которым эмитент продает выпущенные облигации на аукционе. С ОГСЗ можно совершать сделки куп- ли-продажи в течение срока их обращения.
Ценными муниципальными бумагами называются ценные бумаги, выпущенные от имени муниципального образования. Решение об эмитенте ценных муниципальных бумаг Российской Федерации принимает Правительство РФ. Эмитентом ценных муниципальных бумаг выступает исполнительный орган местного самоуправления, действующий на основе устава муниципального образования.
11.8. Дюрация и изгиб
Цена облигации со сроком n , с купонными ежегодными выплатами Rt (ãäå t — номер выплаты, или номер года) и с номиналом N
определяется суммой всех выплат, дисконтированных по ставке r, и является функцией этой ставки. Таким образом, зависимость цены облигации от ставки можно представить в виде соотношения
A(r )= ∑ Rt |
+ N . |
|||
n |
|
|
|
|
t =1 |
(1+r )t |
|
(1+r )n |
|
11. Рынок ценных бумаг и его инструменты |
329 |
По условиям задачи всегда r > −1, Rt ≥ 0 , N > 0 . Поэтому A > 0,
т.е. всегда является величиной положительной. Первая производная цены облигации по ставке дисконтирования определяется выражением
dA |
|
1 |
|
n |
t |
R |
|
n N |
|
|
|
= − |
|
|
∑ |
|
t |
+ |
|
. |
|
dr |
1+r |
(1+r)t |
(1+r)n |
|||||||
|
t=1 |
|
|
|||||||
Эта производная при поставленных выше условиях величина всегда отрицательная. Отсюда следует, что функция A(r ) является убывающей. Вторая производная цены по ставке имеет вид:
d 2 A |
= ∑n |
t (t +1)Rt |
+ |
n(n +1)N |
. |
dr2 |
|
|
|||
t=1 (1+r )t+2 (1+r )t+2 |
|||||
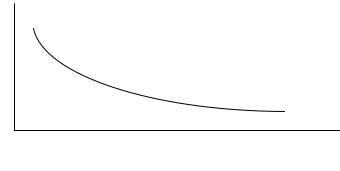
Как следует из этого соотношения, вторая производная всегда положительна. Поэтому исследуемая кривая всегда имеет выпуклость, обращенную вниз так, как показано на рис. 11.10.
Ðèñ. 11.10. Графическая зависимость цены облигации
от процентной ставки
Разложим функцию A(r ) в ряд Тейлора в точке r = r0 , ограни- чившись первыми тремя членами:
|
|
A(r )= A(r0 )+ f ′(r0 )(r −r0 )+ |
f ′′(r0 ) |
(r −r0 )2 |
, |
|
|
|
2 |
||||
|
|
|
|
|
|
|
ãäå f ′(r |
), |
f ′′(r |
) — первая и вторая производные от цены облигации |
|||
0 |
|
0 |
|
|
|
|
по ставке дисконтирования в точке r = r0 .
330 |
III. Фондовый рынок |
Введем замену: |
|
∆A = A(r )− A(r0 ); |
∆r = r −r0 |
и разделим левую и правую части функции для цены облигации на
A0 = A(r0 ). В результате получим |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
∆A |
= |
|
f ′(r0 ) |
∆r + |
|
f ′′(r0 ) |
(∆r)2 . |
|
|||||||||||||
|
|
A |
|
|
|
|
A |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2A |
|
|
|
|
||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
||||
Подставим соотношения для производных в последнюю форму- |
|||||||||||||||||||||||
лу. В результате найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∆A |
|
|
|
|
1 |
|
|
n |
t |
R |
|
|
|
n N |
|
∆r |
|
||||||
|
|
= − |
|
|
|
|
|
∑ |
|
t |
|
+ |
|
|
|
|
|
+ |
|||||
|
|
|
|
|
|
(1+r0 )t |
|
(1+r0 )n |
|
||||||||||||||
A0 |
|
|
|
A0 t=1 |
|
|
|
|
1+r0 |
|
|||||||||||||
+ |
|
1 |
|
∑n |
t (t +1)Rt |
+ |
n(n +1)N |
|
|
(∆r )2 . |
|||||||||||||
|
|
|
(1+r0 )n+2 |
|
|||||||||||||||||||
|
2A0 t=1 (1+r0 )t+2 |
|
|
|
|
|
|||||||||||||||||
Входящие в это выражения величины называются дюрацией:
|
1 |
|
n |
t R |
|
nN |
|
D = |
|
|
∑ |
t |
+ |
|
|
|
(1+r0 )t |
(1+r0 )n |
|||||
|
A0 t=1 |
|
|
||||
è изгибом:
C = |
1 |
∑n |
t (t +1)Rt |
+ |
n(n +1)N |
. |
||
|
|
|
|
(1+r0 )n+2 |
||||
|
2A0 t=1 (1+r0 )t+2 |
|
|
|||||
Используя эти выражения, перепишем формулу для относи- |
||||||||
тельного приращения цены в виде: |
|
|
|
|||||
|
∆A = −D |
∆r |
+C (∆r)2 . |
|
||||
|
|
|
||||||
|
A |
1+r |
|
|
|
|||
|
0 |
|
|
0 |
|
|
|
|
Подставив сюда введенные выше обозначения, получим формулу для цены:
A = A |
1− D |
∆r |
+C (∆r )2 |
. |
|
||||
0 |
|
1+r0 |
|
|
|
|
|
|
11. Рынок ценных бумаг и его инструменты |
|
331 |
|
Если пренебречь изгибом, то формула для цены акции будет |
|||
иметь вид: |
|
|
|
A = A |
1− D |
∆r |
. |
0 |
|
1+r |
|
|
|
0 |
|
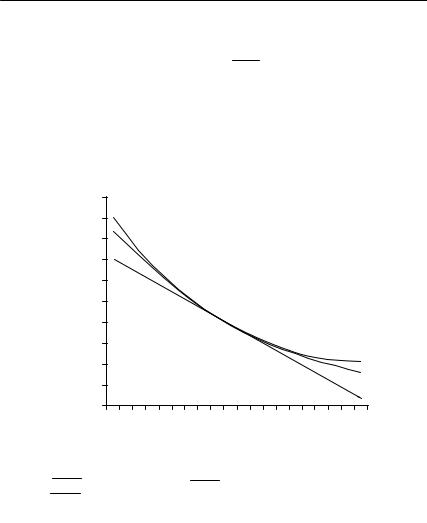
Полученные зависимости в виде графиков представлены на |
|||
рис. 11.11. Сплошная линия — цена облигации, рассчитанная по |
|||
точной формуле. Кривая, представленная точками, — график цены |
|||
облигации с учетом дюрации и изгиба. Прямая пунктирная линия |
|||
соответствует соотношению, в котором учтена только дюрация. Все |
|||
три линии пересекаются в точке (r0, A0 ). |
|
||
Цена облигации A |
|
|
|
Таким образом, при известной дюрации и изгибе по приведенной формуле для относительного изменения цены облигации легко определить изменение этой цены ∆A при незначительном изменении ставки дисконтирования ∆r . При увеличении модуля ∆r ошибка расчета величины изменения цены облигации увеличивается. Если отбросить слагаемое, учитывающее изгиб, то изменение цены облигации при изменении ставки дисконтирования будет определяться только дюрацией, т.е.
∆A |
= −D |
∆r |
. |
A |
|
||
|
1+r |
||
0 |
|
0 |
|
332 |
III. Фондовый рынок |
Как следует из формулы для дюрации, этот показатель является средним взвешенным моментов платежа. Весами являются дисконтированные платежи, деленные на современную стоимость всех платежей. Единицей измерения дюрации является единица измерения времени, т.е. год.
Z Пример 11.12. Бескупонная облигация, имеющая номинал 5000 руб., будет погашена через два года.
Определить цену облигации, дюрацию и изгиб для ставки дисконтирования 10% годовых (точка разложения). Найти изменение цены облигации при изменении ставки дисконтирования на ±2% для трех случаев:
•истинное;
•при учете дюрации и изгиба;
•при учете только дюрации.
Найти методические ошибки расчета цены при учете дюрации и изгиба, а также только дюрации.
Р е ш е н и е. Для определения истинной цены облигации используется полученная формула, которая для бескупонной облигации имеет вид:
A = |
N |
= |
|
5000 |
= 4132, 23 руб. |
|
(1+r0 )nT |
(1 |
+0,1)2 |
||||
0 |
|
|
Преобразовав формулу для дюрации, получим
D = |
1 |
|
nN |
= n. |
|
(1+r0 )n |
|||
|
A0 |
|
||
Таким образом, дюрация для сосредоточенного платежа равна сроку его выплаты. Для нашего случая
D = 2 года.
Изгиб рассчитывается по формуле |
|
|
||||||
C = |
1 |
|
n (n +1)N |
= |
n (n +1) |
= |
2 3 |
= 2, 48. |
2A0 |
t+2 |
2 |
2 |
|||||
|
|
(1+r0 ) |
|
2(1+r0 ) |
2 1,1 |
|||
Истинное изменение цены облигации при изменении ставки дисконтирования на величину ∆r определяется соотношением
|
|
|
|
|
N |
− |
|
|
N |
|
|
|
|
n |
||
∆A |
|
A(r )− A |
(1 |
+r +∆r )n |
(1 |
+r |
)n |
|
1 |
+r |
||||||
|
|
|||||||||||||||
|
= |
0 |
= |
|
0 |
|
|
|
|
0 |
|
= |
|
0 |
|
−1. |
|
|
|
|
N |
|
|
|
|
|
|
|
|||||
A0 |
|
A0 |
|
|
|
|
|
|
|
|
1+r0 +∆r |
|
||||
|
|
|
(1+r0 )n |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
