
- •ВВЕДЕНИЕ
- •1. ОБРАБОТКА РЕЗУЛЬТАТОВ НОРМАТИВНЫХ НАБЛЮДЕНИЙ
- •1.1. Общий порядок организации нормативных наблюдений
- •1.2. Обработка результатов натурных наблюдений. Программа «Natura»
- •1.3. Определение основных характеристик рядов наблюдения. Программа «Sample»
- •2. МНОГОФАКТОРНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ НА ОСНОВЕ БАЗ ДАННЫХ НАБЛЮДЕНИЙ (ИСПЫТАНИЙ). ПРОГРАММА «MODELL»
- •2.1. Шаговый регрессионный метод
- •2.2. Построение доверительных интервалов. Программа «Diagram»
- •3.1. Формулировка задачи
- •3.2. Примеры формулировок экономических задач и их решений при помощи программ «Simply», «Simplint» и «Rasm»
- •4. ТРАНСПОРТНАЯ ЗАДАЧА. ПРОГРАММА «TRANSY»
- •5. ЗАДАЧА КОММИВОЯЖЕРА. ПРОГРАММА «KOMMY»
- •6. ОПТИМИЗАЦИЯ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ. ПРОГРАММА «MARK»
- •7. СЕТЕВОЙ ГРАФИК. ПРОГРАММА «SETY»
- •8. ВАРИАНТЫ ЗАДАЧ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- •Задача 1. Провести обработку результатов нормативных наблюдений и рассчитать новую норму времени на выполнение строительного процесса вручную. Результаты ручного расчета проверить с помощью программы «Natura».
- •Задача 3. В таблицах 8.32 и 8.33 приведены данные по 15 субъектам Российской Федерации о денежных доходах и потребительских расходах на душу.
- •Задача 8. Определение оптимального варианта раскроя арматуры. Произвести раскрой арматурных стержней определенной длины и получить заготовки проектных размеров в необходимых количествах с минимальными отходами при раскрое.
- •9. ПРИЛОЖЕНИЯ. ЛИСТИНГИ ПРИКЛАДНЫХ ПРОГРАММ
- •П1. Листинг программы «NATURA»
- •П2. Листинг программы «SAMPLE»
- •П3. Листинг программы «MODELL»
- •П4. Листинг программы «DIAGRAMM»
- •П5. Листинг программы «SIMPLY»
- •П6. Листинг программы «SIMPLINT»
- •П7. Листинг программы «RASM»
- •П8. Листинг программы «TRANSY»
- •П9. Листинг программы «KOMMY»
- •П10. Листинг программы «MARK»
- •П11. Листинг программы «SETY»
- •РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- •Содержание
- •ВВЕДЕНИЕ
- •1.1. Организационно-технологическая надёжность строительства. Её роль в повышении качества производства работ
- •1.2. Критерии оценки организационно-технологической надежности. Методики их определения
- •1.3. Методики и программы расчета технико-экономических показателей систем машин
- •1.4. Работы по формированию рациональных систем машин
- •1.5. Задачи и подходы к оптимизации распределения систем машин по строительным объектам
- •1.6. Методические и программные средства оценки инвестиционных проектов
- •1.7. Цель и задачи исследований
- •2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ СТРОИТЕЛЬНЫХ МАШИН
- •2.1. Критерии оценки состояния организационно-технологической надежности работы машин
- •2.2. Обработка натурных испытаний строительных машин
- •2.3. Модель надежности инвестиционных проектов
- •2.4. Модель надежности календарного планирования
- •2.5. Модель надежности работы гидротранспортных систем
- •2.6. Модель надежности технологических процессов
- •2.7. Выводы
- •3. ПРОГНОЗИРОВАНИЕ И ОЦЕНКА ОРГАНИЗАЦИОННО-ТЕХНОЛОГИЧЕСКОЙ НАДЕЖНОСТИ РАБОТЫ СИСТЕМ МАШИН
- •3.1. Методологические подходы к прогнозированию и оценке систем
- •3.2. Прогнозирование и оценка организационно-технологической надежности инвестиционных проектов
- •3.3. Прогнозирование и оценка организационно-технологической надежности календарных планов строительства
- •3.4. Прогнозирование и оценка организационно-технологической надежности очередности строительства
- •3.5. Прогнозирование и оценка организационно-технологической надежности работы систем машин
- •3.6. Прогнозирование и оценка организационно-технологической надежности работы комплектов машин для производства земляных работ
- •3.7. Прогнозирование и оценка организационно-технологической надежности работы комплектов машин для производства бетонных работ
- •3.8. Моделирование организационно-технологической надежности работы комплектов машин для перевозки грузов
- •3.9. Прогнозирование и оценка организационно-технологической надежности работы монтажных кранов
- •3.10. Выводы
- •4. ОПТИМИЗАЦИЯ СИСТЕМ МАШИН
- •4.1. Оптимизации парка машин
- •4.2. Оптимизация комплекса машин
- •4.3. Оптимизация очередности выполнения строительных работ
- •4.4. Оптимизация распределения машин в строительстве
- •4.5. Выводы
- •5. РЕКОМЕНДАЦИИ ПО ЭФФЕКТИВНОМУ ИСПОЛЬЗОВАНИЮ СИСТЕМ МАШИН
- •5.2. Оценка организационно-технологической надёжности инвестиционных проектов
- •5.3. Оценка организационно-технологической надёжности календарного планирования
- •5.4. Оценка организационно-технологической надёжности строительного производства на примере земляных работ
- •5.5. Управление организационно-технической надежностью работы строительно-дорожных машин
- •5.6. Выводы
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- •Содержание
- •ВВЕДЕНИЕ
- •1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ ПАРКОВ МАШИН
- •1.3. Оценка надежности инвестиционных проектов
- •1.4. Оценка надежности календарного планирования
- •1.5. Оценка надежности проектных показателей работы машин
- •1.6. Оценка надежности технологических процессов
- •2.1. Методологические подходы к моделированию
- •2.2. Моделирование организационно-технологической надежности инвестиционных проектов
- •2.3. Моделирование организационно-технологической надежности календарных планов строительства
- •2.4. Моделирование организационно-технологической надежности очередности строительства
- •2.5. Моделирование организационно-технологической надежности работы парков машин
- •2.6. Моделирование организационно-технологической надежности работы комплектов машин для производства земляных работ
- •2.7. Моделирование организационно-технологической надежности работы комплектов машин для производства бетонных работ
- •2.8. Моделирование организационно-технологической надежности работы комплектов машин для перевозки грузов
- •2.9. Моделирование организационно-технологической надежности работы монтажных кранов
- •3. ОПТИМИЗАЦИЯ КОЛИЧЕСТВА И ТИПОВ МАШИН, СОСТАВЛЯЮЩИХ ПАРК МАШИН
- •3.1. Методика оптимизации составов парка машин
- •3.2. Оптимизация комплекса машин
- •3.3. Формирование ресурсосберегающего комплекса машин
- •3.4. Оптимизация очередности выполнения механизированных объёмов на строительных объектах
- •3.5. Оптимальное распределение машин в строительстве
- •4.1. Возможности методического и программного обеспечения
- •4.2. Модели организационно-технологической надёжности инвестиционных проектов
- •4.3. Модели организационно-технологической надёжности календарного планирования
- •4.4. Модели организационно-технологической надёжности строительного производства на примере земляных работ
- •4.5. Управление организационно-технической надежностью работы строительно-дорожных машин
- •4.6. Рекомендации по определению эффективности применения новых строительных машин и механизмов
- •ЗАКЛЮЧЕНИЕ
- •Содержание
- •ВВЕДЕНИЕ
- •1.1. Оценка надежности работы строительных машин
- •1.2. Оценка организационно-технологической надежности работы строительных машин
- •1.3. Действующие методики расчета технико-экономических показателей проектных решений
- •1.5. Защита свай от коррозии
- •2. ОБОСНОВАНИЕ СПОСОБОВ ПОГРУЖЕНИЯ СВАЙ
- •2.1. Моделирование погружения свай
- •2.2. Модели способов погружения свай
- •2.3. Влияние условий производства работ на экономическую эффективность свайно-бурового производства
- •2.4. Анализ показателей производства свайных работ
- •3. ОБОСНОВАНИЕ КОМПЛЕКСА МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ
- •3.1. Автоматизация проектирования технологических процессов
- •3.2. Алгоритм обоснования способов погружения свай
- •3.3. Выводы
- •4. ФОРМИРОВАНИЕ РЕСУРСОСБЕРЕГАЮЩИХ ПАРКОВ, КОМПЛЕКСОВ И КОМПЛЕКТОВ СТРОИТЕЛЬНЫХ МАШИН
- •4.1. Общий подход
- •4.2. База технических и экономических показателей строительных машин и механизмов
- •4.3. База данных по организационно-технологической надёжности
- •4.4. База справочной информации для организационно-технологических расчётов
- •4.5. Выводы
- •5. ОЦЕНКА ТЕХНИЧЕСКОЙ НАДЕЖНОСТИ РАБОТЫ БУРОВЫХ СТАНКОВ
- •6. МОДЕЛИРОВАНИЕ НАДЕЖНОСТИ РАБОТЫ БУРОВЫХ СТАНКОВ
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- •Содержание
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- •1.1. Строительство как отрасль материального производства
- •1.2. Трудовые ресурсы отрасли (строительные организации и фирмы)
- •1.3. Возникновение и развитие науки «Организация, планирование и управление строительством»
- •2. НАУЧНЫЕ ОСНОВЫ ОРГАНИЗАЦИИ СТРОИТЕЛЬСТВА
- •2.1. Основные термины и понятия организации строительства
- •2.3. Понятие «инвестиционный проект» и управление проектом
- •3. ПОДГОТОВКА СТРОИТЕЛЬНОГО ПРОИЗВОДСТВА
- •3.1. Организационно-техническая подготовка к строительству
- •3.2. Организация проектно-изыскательских работ для строительства
- •4. МОДЕЛИРОВАНИЕ ОРГАНИЗАЦИИ СТРОИТЕЛЬНОГО ПРОИЗВОДСТВА
- •4.1. Понятие и виды организационно-технологических моделей строительства
- •4.2. Моделирование поточного строительства
- •4.2.1. Сущность поточной организации строительства
- •4.2.2. Классификация строительных потоков
- •4.2.3. Параметры строительных потоков
- •4.2.4. Моделирование ритмичных строительных потоков
- •4.2.5. Моделирование неритмичных строительных потоков
- •4.2.6. Установление оптимальной очередности возведения объектов
- •4.3. Моделирование строительства на основе системы сетевого планирования и управления строительством
- •4.3.2. Основные понятия метода СПУ и элементы сетевых моделей
- •4.3.3. Классификация сетевых графиков
- •4.3.4. Правила построения сетевых моделей
- •4.3.5. Расчетные параметры сетевых графиков и формулы их определения
- •4.3.6. Расчет сетевых графиков и построение их в масштабе времени
- •4.3.7. Корректировка и оптимизация сетевых графиков
- •5. ПРОЕКТИРОВАНИЕ ОРГАНИЗАЦИИ СТРОИТЕЛЬСТВА
- •5.1. Разработка проекта организации строительства (ПОС)
- •5.1.1. Характеристика исходных данных
- •5.1.3. Определение потребности в материально-технических, трудовых и водо-энергетических ресурсах
- •5.1.3.1. Расчет потребности в строительных материалах, конструкциях и полуфабрикатах
- •5.1.3.2. Расчет потребности в водо-энергетических ресурсах
- •5.1.3.3. Определение затрат труда
- •5.1.4. Выбор организационно-технологических схем возведения зданий
- •5.1.5. Выбор методов организации работ
- •5.1.6. Составление сводного календарного плана строительства (СКПС). Составление календарного плана подготовительного периода
- •5.1.6.2. Расчет параметров комплексного потока строительства промышленного предприятия
- •5.1.7. Разработка стройгенпланов на основной и подготовительный периоды строительства с расчетом строительного хозяйства
- •5.1.8. Охрана труда и противопожарные мероприятия
- •5.1.9. Технико-экономическая оценка ПОС
- •6. РАЗРАБОТКА ПРОЕКТА ПРОИЗВОДСТВА РАБОТ (ППР) НА ОБЪЕКТЕ
- •6.1. Характеристика исходных данных и объекта строительства
- •6.2. Подсчет объемов работ
- •6.3. Выбор методов производства работ, основных строительных машин и механизмов
- •6.3.1. Земляные работы.
- •6.3.2. Возведение подземной и надземной частей здания
- •6.4. Определение трудоемкости работ
- •6.5. Календарное планирование
- •6.5.1. Проектирование линейного графика
- •6.5.2. Проектирование циклограммы
- •6.5.3. Проектирование сетевого графика
- •6.6. Проектирование стройгенплана объекта с расчетом строительного хозяйства
- •6.6.1. Потребность во временных зданиях и сооружениях
- •6.6.2. Определение площадей складов
- •6.6.3. Водоснабжение строительной площадки
- •6.6.4. Электроснабжение строительной площадки
- •6.6.5. Снабжение строительства сжатым воздухом
- •6.7. Мероприятия по охране труда и противопожарной безопасности
- •6.8. Технико-экономическая оценка ППР
- •7. ОРГАНИЗАЦИЯ МАТЕРИАЛЬНО-ТЕХНИЧЕСКОГО ОБЕСПЕЧЕНИЯ СТРОИТЕЛЬСТВА
- •7.1. Понятие и масштабы материально-технической базы строительства.
- •7.2. Организация и источники поставок материально-технических ресурсов
- •7.3. Понятие логистики
- •7.4. Учет и контроль расхода материалов
- •7.5. Организация производственно-технологической комплектации строящихся объектов
- •8. ОРГАНИЗАЦИЯ И ЭКСПЛУАТАЦИЯ СТРОИТЕЛЬНЫХ МАШИН
- •8.1. Основные положения и понятия
- •8.2. Организационные формы эксплуатации парка строительных машин
- •9. ОРГАНИЗАЦИЯ ТРАНСПОРТА НА СТРОИТЕЛЬСТВЕ
- •9.1. Общие положения
- •9.2. Организация автотранспорта на строительстве
- •Библиографический указатель
- •ВВЕДЕНИЕ
- •1. СУЩНОСТЬ УПРАВЛЕНИЯ СТРОИТЕЛЬНЫМ ПРОИЗВОДСТВОМ
- •1.1. Сущность понятия «управление строительством»
- •1.2. Строительство как производственная система
- •1.3. Управляющая и управляемая подсистемы
- •2.1. Закономерности управления
- •2.2. Принципы управления
- •3. ОРГАНИЗАЦИЯ УПРАВЛЕНИЯ
- •3.1. Процесс управления
- •3.2. Функции управления
- •4. ОРГАНИЗАЦИЯ СИСТЕМ УПРАВЛЕНИЯ
- •4.1. Требования к системам управления
- •4.2. Типы организационных структур управления
- •4.3. Организационные формы и структура управления отраслью
- •4.4. Виды подрядных строительно-монтажных организаций
- •4.5. Организационная структура аппарата управления строительных организаций
- •5. ТЕХНОЛОГИЯ И ТЕХНИКА УПРАВЛЕНИЯ
- •5.1. Управленческая информация ее виды
- •5.2. Техника управления
- •6. УПРАВЛЕНЧЕСКИЕ РЕШЕНИЯ
- •6.1. Роль управленческих решений в процессе управления
- •6.3. Субъективные недостатки решений и пути их устранения
- •6.4. Организация принятия и реализации управленческих решений
- •7. МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
- •7.1. Системный подход
- •7.2. Моделирование систем
- •7.3. Системный анализ
- •7.4. Экспертные методы принятия решения
- •7.5. Логические и логико-математические методы принятия решений
- •8. СТИЛИ И МЕТОДЫ УПРАВЛЕНИЯ
- •8.1. Социально-психологические аспекты управления
- •8.2. Стили управления
- •8.3. Типичные недостатки работников сферы управления
- •8.4. Методы управления
- •9. ОПЕРАТИВНОЕ УПРАВЛЕНИЕ СТРОИТЕЛЬНЫМ ПРОИЗВОДСТВОМ
- •9.1. Общие положения
- •9.2. Разработка месячных оперативных планов
- •9.3. Недельно-суточное оперативное планирование
- •9.4. Диспетчерское управление в строительстве
- •10.1. Научные основы управления качеством строительства
- •10.2. Система контроля качества в строительстве
- •10.3. Организация приемки объектов в эксплуатацию
- •Библиографический указатель
- •Содержание
4.3.5. Расчетные параметры сетевых графиков и формулы их определения
Расчет сетевого графика заключается в нахождении времени начала и окончания каждой из работ, продолжительности критического пути и работ, его составляющих, а также резервов времени всех некритических работ. Расчет сетевых графиков необходим для установления перечня работ, лежащих в пределах критической зоны, выявления влияния изменений отдельных работ на общий срок строительства, для проверки и анализа графика в процессе строительства.
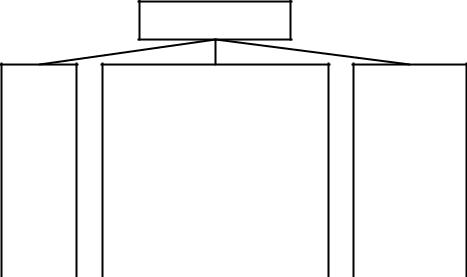
Сетевые графики характеризуются рядом расчетных параметров, классификация и обозначения которых приведены на рисунке 4.19.
Расчетные параметры сетевых графиков
Основные |
Параметры работ |
Параметры событий |
ti− j |
Tкр |
|
Ti−рнj |
T |
−ро |
T |
пн− |
Ti−поj |
Ri− j |
ri− j |
|
T р |
T п |
t |
п |
|
|
|
|
i |
j |
i |
j |
|
|
|
|
i |
i |
|
i |
Продолжительность работы |
Продолжительность критического пути |
|
Время раннего начала работ |
Время раннего окончания работ |
Время позднего начала работ |
Время позднего окончания работ |
Общий резерв времени работы |
Частный резерв времени работы |
|
Время раннего свершения событий |
Время позднего свершения событий |
Потенциал событий |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.19. Классификация и обозначение параметров сетевых графиков
Продолжительность любой работы определяется временем, не-
обходимым для её выполнения. В детерминированных графиках продолжительность работ устанавливается жёстко. При механизированном их выполнении она определяется по формуле (4.13), а при выполнении работы вручную – по формуле (4.14).
tмех = P / П |
n α , |
(4.13) |
||
i− j |
i |
|
э.см. см |
|
t руч |
= PH |
вр.i |
/ N n α , |
(4.14) |
i− j |
i |
i см. |
|
|
где Рi – объем i-го вида работ в физических единицах измерения; Пэ. см – эксплуатационная сменная производительность механизма; nсм – число смен работы в сутках;
α = 1–1,2 – коэффициент перевыполнения норм;
77
Нврi – норма затрат труда на выполнение единицы объема работ i-го вида;
Ni – сменный состав бригады на i-том виде работ.
В вероятностных графиках продолжительность работ чаще всего определяется методом усреднения полученных экспертных оценок, суть которого состоит в нахождении математического ожидания про-
должительности работ « tiож− j ». В роли экспертов выступают специалисты, имеющие опыт практической работы.
tiож− j = (tiоп− j + 4tiнв− j +tiпес− j ) / 6 , |
(4.15) |
где tiоп− j – оптимистическая (минимальная) оценка продолжительности
работы, данная в предположении наиболее благоприятного стечения обстоятельств;
tiнв− j – наиболее вероятная (реалистическая) оценка продолжительности
работы, данная в предположении наиболее часто встречающихся обстоятельств;
tiпес− j – пессимистическая (максимальная) оценка продолжительности
работы, данная в предположении наиболее неблагоприятного стечения обстоятельств.
Если не удается получить от экспертов реалистическую оценку, то можно использовать только две оценки:
tiож− j = (3tiоп− j + 2tiпес− j ) /5 . |
(4.16) |
После усреднения вероятностная сеть рассматривается как детерминированная, в которой использованы временные оценки работ, найденные по формулам (4.15) или (4.16).
Продолжительность критического пути определяется как наибольшая сумма продолжительностей работ, составляющих полные пути графика, или по формуле (4.17).
T |
= maxT ро , |
(4.17) |
кр |
i−z |
|
где z – номер завершающего события;
Ti−роz – раннее окончание работы, заканчивающейся последним
событием.
Ранним началом работы является самый ранний из возможных сроков её начала, обусловленный окончанием непосредственно предшествующих ей работ:
T рн = maxT ро = max(T рн + t |
h−i |
) = T р |
, (4.18) |
||
i− j |
h−i |
h−i |
i |
|
|
где maxThро−i – максимальное значение времени раннего окончания работ, предшествующих данной.
78
Время раннего начала работы соответствует времени раннего свершения i-го события, т. е. начального для данной работы событияTi p ,
т. к. любое событие может считаться свершившимся лишь после окончания всех предшествующих ему работ.
Ранним окончанием работы Ti−роj является самый ранний из воз-
можных сроков её окончания при условии начала данной работы тоже в самый ранний срок:
T ро = T рн |
+t |
i− j |
. |
(4.19) |
|
i− j |
i− j |
|
|
|
|
Расчет ранних параметров работ производят последовательно ходом от исходного события графика к завершающему. Для работ, начинающихся с исходного события графика, время раннего начала принимается равным нулю. Поскольку время раннего начала любой работы представляет собой величину наибольшего по продолжительности пути от исходного до i-го события графика, то, дойдя до завершающего z-го события, можно установить продолжительность критического пути Ткр по формуле (4.17) уже при расчете ранних параметров.
Поздним началом работы Tiпн− j является самый поздний срок её
начала, не вызывающий увеличения продолжительности критического пути:
T пн |
= T по |
−t |
i− j |
. |
(4.20) |
i− j |
i− j |
|
|
|
Поздним окончанием работы Tiпо− j является самый поздний допу-
стимый срок её окончания, не вызывающий увеличения продолжительности критического пути:
T по |
= minT пн |
= min(T по |
−t |
j −k |
) = T п , |
(4.21) |
i− j |
j −k |
j −k |
|
j |
|
где min Tjпн−k – минимальное значение из поздних начал работ, непо-
средственно последующих за данной работой.
Расчет поздних параметров работ производят последовательно ходом от завершающего события графика к исходному. Для завершающего z-го события характерно следующее условие:
T |
= maxT ро = maxT по |
= T |
р = T п . |
(4.22) |
|
кр |
i−z |
i−z |
z |
z |
|
Общим резервом времени работы Ri-j называют максимальный промежуток времени, на который можно отдалить окончание данной работы за счет увеличения её продолжительности или задержки начала, не изменяя продолжительности критического пути:
R |
i− j |
=T по |
−T ро =T пн |
−T рн . |
(4.23) |
|
|
i− j |
i− j |
i− j |
i− j |
|
|
Общий резерв времени имеют все некритические работы сетевого графика.
79
Частным резервом времени работы называют максимальный промежуток времени, на который можно отдалить окончание данной работы за счет увеличения её продолжительности или задержки начала, не изменяя при этом раннего начала последующих работ:
r |
= T рн |
−T ро = T рн |
−(T рн |
+t |
i− j |
) , |
(4.24) |
|
i− j |
j −k |
i− j |
j −k |
i− j |
|
|
|
|
где Tjрн−k – время раннего начала последующих работ по отношению к
данной работе.
Частный резерв времени имеет место, когда одним событием заканчивается не менее двух работ. Величина частного резерва времени не может быть больше величины общего резерва времени для той же работы:
ri− j ≤ Ri− j . |
(4.25) |
Потенциалом i-го события tiп называют путь максимальной про-
должительности от i-го события до завершающего z-го события. Расчет потенциалов событий ведут ходом от завершающего события к исходному. Потенциал завершающего события равен нулю, а потенциал исходного – продолжительности критического пути. Потенциал любого промежуточного события определяют по формуле (4.25):
tiп = max(tпj +ti− j ) , |
(4.26) |
где tпj – потенциал последующего по отношению к i-му события.
4.3.6. Расчет сетевых графиков и построение их в масштабе времени
В отечественной практике применения системы сетевого планирования и управления строительством используются как ручные способы расчета временных параметров сетевых графиков, так и машинный. Изучение способов ручного расчета позволяет студентам детально узнать, освоить и запомнить алгоритм и применять его для решения конкретных задач сетевого планирования. Вручную рассчитывают сетевые графики с числом работ до 300–500 (в зависимости от плотности сети). При большей размерности сетевых графиков используют машинный способ расчета (на ПЭВМ).
Расчет временных параметров сетевых графиков можно выполнить табличным или секторным способами, а также методом «дроби» или методом потенциалов.
Табличный способ является самым полным и может применяться как для ручного, так и для машинного расчета, для его использования необходимы:
• систематизация нумерации событий (т. е. в графике не должно быть пропущенных или повторяющихся номеров событий, и для лю-
80
бой работы номер конечного события всегда должен быть больше номера начального события);
•систематизация записи работ. Коды всех работ (включая и зависимости) записывают последовательно в порядке возрастания номера начального события (т. е. записывают сначала коды всех работ, начинающихся первым событием, затем коды всех работ, начинающихся вторым событием и т. д.);
•использование специальной формы таблицы.
Исходными данными для расчета временных параметров сетевого графика считаются: номера строк таблицы (или порядковые номера работ и их количество); коды работ; продолжительность каждой работы; обратный адрес, указывающий место записи в таблице работ, предшествующих данной и их количество. Исходные данные записывают в первые четыре колонки расчетной таблицы. После записи исходных данных расчет временных параметров сетевого графика можно вести только по таблице, не заглядывая в график и используя формулы
(4.18)–(4.26).
Непосредственный расчет параметров работ сетевого графика (таблица 4.9) производят в три этапа:
•расчет ранних параметров «прямым ходом» (т. е. от исходного события графика к завершающему или сверху вниз по таблице). В результате «прямого хода» определяют время раннего начала и раннего окончания каждой работы и продолжительность критического пути;
•расчет поздних параметров «обратным ходом» (т. е. от завершающего события графика к исходному или снизу вверх по таблице). В результате «обратного хода» определяют время позднего начала и позднего окончания каждой работы и выполняют проверку «прямого хода» (т. е. позднее начало хотя бы одной из работ, начинающихся исходным событием должно получиться равным нулю);
•расчет резервов времени работ. Этот расчет может выполняться с любой строки и в любом направлении.
Для большей наглядности рассмотрим конкретный пример расчета сетевой модели, показанной на рисунке 4.11.
В процессе заполнения расчетной таблицы можно проверить правильность расчета следующим образом:
•ранние параметры каждой работы должны быть меньше или равны соответствующим поздним;
•позднее начало хотя бы одной из работ, начинающихся исходным событием должно получиться равным нулю;
81
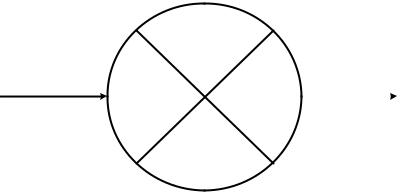
Таблица 4.9. Табличный расчет сетевого графика
Номера |
Обрат- |
Код |
Продол- |
|
Временные параметры работ |
|
Крити- |
|||
строк |
ный |
работ |
житель- |
ранние |
поздние |
резервы |
ческие |
|||
|
адрес |
|
ность |
нача- |
окон- |
окон- |
нача- |
общий |
част- |
работы |
|
|
|
работ |
ло |
чание |
чание |
ло |
|
ный |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- |
1-2 |
6 |
0 |
6 |
6 |
0 |
0 |
0 |
к |
2 |
- |
1-3 |
4 |
0 |
4 |
8 |
4 |
4 |
2 |
- |
3 |
- |
1-4 |
5 |
0 |
5 |
18 |
13 |
13 |
8 |
- |
4 |
1 |
2-3 |
0 |
6 |
6 |
8 |
8 |
2 |
0 |
- |
5 |
1 |
2-5 |
10 |
6 |
16 |
16 |
6 |
0 |
0 |
к |
6 |
1 |
2-6 |
11 |
6 |
17 |
27 |
16 |
10 |
0 |
- |
7 |
2, 4 |
3-4 |
7 |
6 |
13 |
18 |
11 |
5 |
0 |
- |
8 |
2, 4 |
3-5 |
8 |
6 |
14 |
16 |
8 |
2 |
2 |
- |
9 |
3, 7 |
4-7 |
12 |
13 |
25 |
30 |
18 |
5 |
5 |
- |
10 |
5, 8 |
5-6 |
0 |
16 |
16 |
27 |
27 |
11 |
1 |
- |
11 |
5, 8 |
5-7 |
14 |
16 |
30 |
30 |
16 |
0 |
0 |
к |
12 |
6, 10 |
6-7 |
3 |
17 |
|
30 |
27 |
10 |
10 |
- |
13 |
9,11,12 |
7… |
|
30 |
|
|
|
|
|
|
•критический путь должен представлять собой непрерывную последовательность работ и зависимостей от исходного события до завершающего;
•величина частного резерва времени каждой работы должна быть меньше или равна величине общего резерва времени той же работы.
Работы критического пути резервов времени не имеют, для них и частный, и общий резервы равны нулю (отсюда и название – критический путь), что позволяет легко выявить их по таблице и выделить на сети.
Секторный способ предусматривает возможность расчета временных параметров сетевого графика непосредственно на сети. Для его использования каждое событие графика вычерчивается крупнее и делится двумя взаимно перпендикулярными диаметрами на четыре одинаковых сектора. Параметры, записываемые в секторах, показаны на рисунке 4.20.
|
|
Номер |
|
|
|
|
данного |
|
|
|
|
события |
|
|
Предшествующая |
|
i |
|
Последующая |
|
|
|
||
работа |
Время раннего |
|
Время позднего |
работа |
h - i |
|
i - j |
||
|
начала работы |
|
окончания работы |
|
|
|
|
||
|
Ti−рнj |
Номер |
T по |
|
|
|
h−i |
|
|
события, через которое к данному идет путь наибольшей продолжительности от исходного
Рисунок 4.20. Изображение событий при расчете сети секторным способом
82
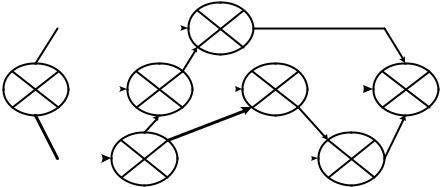
Сам расчет производят в следующей последовательности:
•производят нумерацию событий, заполняя верхний сектор всех событий ходом от исходного события к завершающему;
•определяют ранние начала всех работ по формуле (4.18), заполняя левый сектор всех событий ходом от исходного события к завершающему. Одновременно с этим, идя в том же направлении, заполняют нижний сектор всех событий;
•определяют поздние окончания всех работ по формуле (4.21), заполняя правый сектор всех событий ходом от завершающего события к исходному;
•определяют резервы времени всех работ по формулам (4.23) и (4.24), записывая их в отдельной таблице или непосредственно на графике рядом с соответствующей работой.
Пример расчета временных параметров сетевого графика секторным способом приведен на рисунке 4.21.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
13 |
|
|
|
18 |
|
|
12 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
13 |
|
|
|
|
|
8 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
0 |
|
|
4 |
|
|
|
|
|
6 |
8 |
8 |
|
|
|
16 |
|
16 |
|
14 |
|
|
30 |
30 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
- |
|
|
4 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
1 |
|
|
10 |
|
|
10 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
17 |
|
27 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
10 |
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рисунок 4.21. Пример расчета сетевого графика секторным способом
Работы критического пути при расчете сети секторным способом могут быть определены по событиям, в которых значения параметров левого и правого секторов равны между собой.
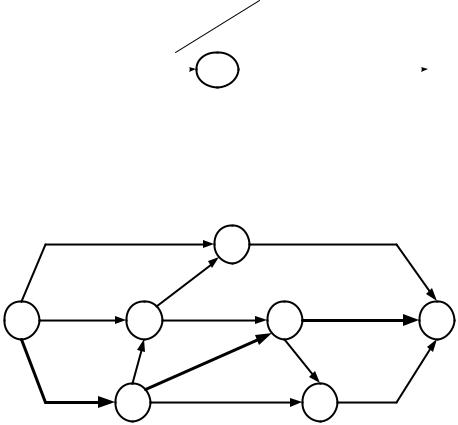
Метод «дроби» представляет собой ускоренный (и сокращенный) способ расчета временных параметров сетевого графика прямо на сети. Он является наименее трудоемким из всех существующих способов расчета сетевых графиков. При этом методе расчета в числителе дроби, проставляемой рядом с каждым событием, определяют по формуле (4.18) и записывают время раннего начала работ, начинающихся с данного события, а в знаменателе – время позднего окончания работ, заканчивающихся данным событием, найденное по формуле (4.21). Параметры, записываемые в числителе и знаменателе дроби, показаны на рисунке 4.22, а пример расчета сетевого графика методом «дроби» приведен на рисунке 4.23.
83
|
T рн |
|
|
|
|
Время раннего |
|
i− j |
|
по |
Время позднего |
начала работы |
|
|
Th−i |
окончания работы |
|
i - j |
|
i |
|
|
h - i |
|
|
|
|
|
|
Предшествующая |
|
|
|
Последующая |
|
|
|
|
|
||
работа |
|
|
|
|
работа |
h - i |
|
|
|
|
i - j |
Рисунок 4.22. Параметры, записываемые при расчете сети методом «дроби»
|
|
5 |
13/18 |
|
12 |
|
|
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
0/0 |
|
6/8 |
7 |
|
16/16 |
|
30/30 |
|
|
|
|
||||
|
|
|
|
|
|
||
1 |
4 |
3 |
8 |
5 |
|
14 |
7 |
|
|
|
|
||||
|
|
|
10 |
|
|
|
|
|
6 |
6/6 |
|
11 |
|
17/27 |
3 |
|
2 |
|
6 |
|
|||
|
|
|
|
|
|
Рисунок 4.23. Пример расчета сетевого графика методом «дроби»
Работы критического пути, выделенные на рисунке 4.23 жирными стрелками, определяют по событиям, у которых значения параметров в числителе и знаменателе дроби равны между собой.
Метод потенциалов предусматривает возможность оценки времени, оставшегося после свершения каждого события, до завершения всех работ. Для использования этого метода рядом с каждым событием (или внутри события) вычерчивают Х-образный знак, в который записывают расчетные параметры (рисунок 4.24).
84
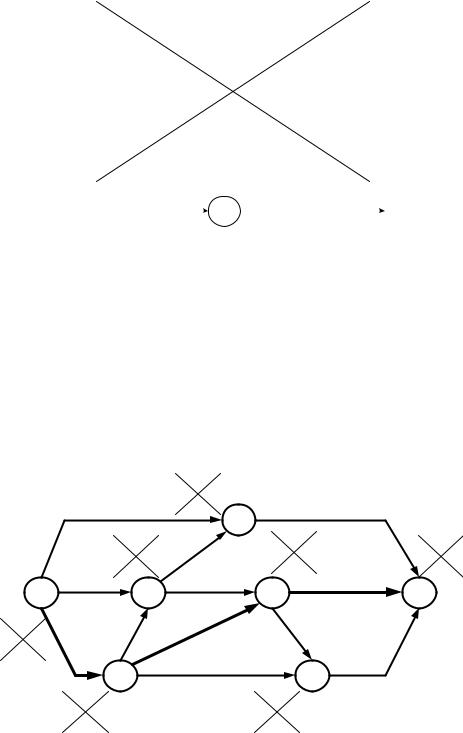
Номер события, через |
|
|||
которое к завершающему |
||||
идет путь наибольшей |
|
|||
продолжительности от |
|
|||
Время раннего |
|
данного |
|
|
|
|
|
|
|
начала работы |
|
|
|
Потенциал |
i - j |
|
|
|
i-го события |
Ti−рнj |
|
Номер |
tiп |
|
|
события, через |
|
||
которое к данному идет |
|
|||
|
путь наибольшей |
|
||
продолжительности от |
|
|||
|
|
исходного |
|
|
|
|
i |
|
|
Предшествующая |
|
Последующая |
||
|
|
|||
работа |
|
|
|
работа |
h - i |
|
|
|
i - j |
Рисунок 4.24. Обозначение параметров при расчете сети методом потенциалов
Непосредственный расчет выполняют в два этапа:
•на первом этапе расчета заполняют левый и нижний секторы ходом от исходного события к завершающему, используя формулу (4.18);
•на втором этапе расчета заполняют правый и верхний секторы, идя «обратным» ходом и используя формулу (4.26).
Пример сетевого графика, рассчитанного методом потенциалов, приведен на рисунке 4.25.
|
|
|
|
7 |
|
|
|
|
|
|
|
|
13 |
|
12 |
|
|
|
|
|
|
5 |
|
3 |
4 |
12 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
7 |
|
|
- |
|
|
|
|
16 |
14 |
|
|
||
|
6 |
22 |
7 |
|
|
30 |
0 |
||
|
|
|
2 |
|
|||||
|
|
2 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||
1 |
4 |
3 |
|
8 |
5 |
|
14 |
7 |
|
|
|
|
|
|
|
2 6
0 30
-
|
2 |
11 |
|
6 |
3 |
|
|
|
|
||
|
5 |
|
|
7 |
|
6 |
24 |
|
17 |
3 |
|
|
1 |
|
|
2 |
|
Рисунок 4.25. Пример расчета сети методом потенциалов
85
Работы критического пути определяют по событиям, у которых сумма параметров, записанных в левом и правом секторах, равна величине критического пути.
При расчете сетевого графика непосредственно на сети требуется меньше времени, чем при расчете табличным способом, уменьшается вероятность механических ошибок. Но так как расчет делается на сети, то сетевой график в этом случае становится перегруженным записью большого количества данных и трудно читается. Поэтому расчеты непосредственно на графике рекомендуется производить на первой стадии составления графика, а также в процессе выполнения предварительных расчетов в ходе строительства.
Рассчитанный сетевой график, построенный без учета временного масштаба, затрудняет установление комплекса работ, выполняемых в определенный период времени, установление их опережения или отставания, осложняет перераспределение ресурсов и определение потребного их количества в определенное время. Эти недостатки легко ликвидируются в случае построения графика в масштабе времени (или его календаризации).
Построение сетевого графика в масштабе времени производят по ранним началам или по поздним окончаниям работ. Если график строят по ранним началам работ, то его события наносят по найденным срокам раннего начала работ. Проекция любой стрелки-работы на временную ось в этом случае равна сумме продолжительности работы и её частного резерва времени. Если график строят по поздним окончаниям работ, то проекция стрелки-работы на временную ось равна сумме продолжительности работы и части её общего резерва времени, оставшейся после использования общих резервов времени на всех предшествующих работах.
Построение сетевого графика в масштабе времени рекомендуется начинать с нанесения критического пути, продолжительность которого определяет общий срок строительства, затем наносят все остальные работы. Рядом с каждой работой, имеющей частный резерв времени, указывается его величина. Примеры сетевого графика, построенного в масштабе времени, показаны на рисунке 4.26.
Если рядом с каждой работой проставить данные о потреблении различных видов ресурсов, то с помощью масштабного сетевого графика можно легко построить диаграммы расходования того или иного вида ресурсов (трудовых, материальных, финансовых) и сопоставить этот расход с фактическим наличием ресурсов.
86
