
Metod (2529)
.pdfВВЕДЕНИЕ
Студенты-заочники специальностей «Подъемно-транспортные, строительные, дорожные машины и оборудование» и «Строительство железных дорог» (ускоренное обучение) изучают дисциплину «Теоретическая механика» во 2-м и 3-м семестрах.
Во 2-м семестре изучается «Статика твердого тела» и «Кинематика точки и тела», выполняются и защищаются контрольные работы № 1 и № 2. Итоговый контроль — экзамен.
В3-м семестре изучается «Динамика материальной точки и механической системы», выполняется и защищается контрольная работа № 3. Итоговый контроль — экзамен.
Выбор заданий контрольных работ производится с помощью таблицы по двум последним цифрам учебного шифра: задачи № 1 и
№3 выбираются по последней цифре шифра, а задача № 2 — по предпоследней цифре.
Встолбцах таблицы указаны номера задач соответствующих заданий в сборнике задач по теоретической механике И.В. Мещерского 1981 г. выпуска (в скобках указаны номера этих же задач в сборниках более ранних изданий). Задачи С-3, С-4, К-4, Д-10 студент выбирает из методических указаний по выполнению контрольных работ студентами-заочниками под редакцией С.М. Тарга 1989 г. выпуска.
Номер рисунка в задачах С-3, С-4, К-4, Д-10 выбирается по предпоследней цифре шифра, а номер строки с данными к задаче определяется по соответствующим таблицам, которые приводятся в текстах задач, — по последней.
3
Таблица выбора вариантов заданий контрольных работ
Контрольная работа № 1 |
Контрольная работа № 2 |
Контрольная работа № 3 |
|||||||
(Задачи 1 , 2 |
+ С-3, С-4) |
(Задачи 1 , 2 , 3 |
+ К-4) |
(Задачи 1 , 2 , 3 |
+ Д-10) |
||||
Цифра шифра |
№ 1 по послед. цифре шифра |
№ 2 по предпосл. цифре шифра |
№ 1 по послед. цифре шифра |
№ 2 по предпосл. цифре шифра |
№ 3 по послед. цифре шифра |
№ 1 по послед. цифре шифра |
№ 2 по предпосл. Цифре шифра |
|
№ 3 по послед. цифре шифра |
|
|
|
|
|
|
|
|
|
|
0 |
4.8 |
9.5 |
11.5 |
12.2 |
16.17 |
26.1 |
27.2 |
|
38.13 |
(11.6) |
|
(38.12) |
|||||||
|
|
|
|
|
|
|
|
||
1 |
4.9 |
9.7 |
11.3 |
12.7 |
16.18 |
26.2 |
27.4 |
|
38.14 |
(12.8) |
|
(38.13) |
|||||||
|
|
|
|
|
|
|
|
||
2 |
4.10 |
9.8 |
11.4 |
12.6 |
16.19 |
26.3 |
27.5 |
|
38.20 |
(11.5) |
(12.7) |
|
|||||||
|
|
|
|
|
|
|
|
||
3 |
4.25 |
9.9 |
10.14 |
12.9 |
16.21 |
26.5 |
27.8 |
|
38.24 |
(10.15) |
(12.10) |
|
|||||||
|
|
|
|
|
|
|
|
||
4 |
4.26 |
9.10 |
10.12 |
12.13 |
16.22 |
26.6 |
27.3 |
|
38.27 |
(12.14) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
5 |
4.27 |
9.11 |
10.19 |
12.15 |
16.24 |
26.10 |
27.21 |
|
38.30 |
(10.20) |
(12.16) |
(27.22) |
|
(38.31) |
|||||
|
|
|
|
|
|
||||
6 |
4.29 |
9.12 |
10.4 |
12.14 |
16.29 |
26.22 |
27.30 |
|
38.31 |
(1) |
(12.15) |
(16.30) |
(27.31) |
|
(38.32) |
||||
|
|
|
|
|
|||||
7 |
4.15 |
9.18 |
10.4 |
12.21 |
16.31 |
26.24 |
27.31 |
|
38.38 |
(2) |
(12.22) |
(16.32) |
(27.32) |
|
(38.39) |
||||
|
|
|
|
|
|||||
8 |
4.11 |
9.19 |
10.13 |
12.22 |
16.32 |
26.26 |
27.7 |
|
38.40 |
(10.14) |
(12.23) |
|
(38.41) |
||||||
|
|
|
|
|
|
|
|||
9 |
4.22 |
9.20 |
10.4 |
12.24 |
16.35 |
26.13 |
27.40 |
|
38.7 |
(4) |
(12.25) |
(16.34) |
(27.42) |
|
|||||
|
|
|
|
|
|
||||
4
1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ, ВХОДЯЩИХ В КОНТРОЛЬНУЮ РАБОТУ № 1
Задача № 1 посвящена определению реакций опор твердого тела, находящегося в равновесии под действием произвольной плоской системы сил.
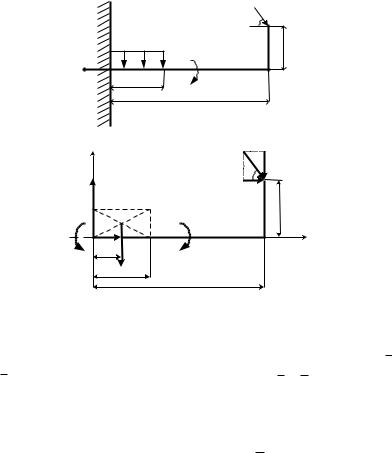
Пример 1.1. Определить реакцию заделки угольника АВС в стену (рис. 1.1).
|
|
|
60 o |
Р=2Н |
|
|
|
|
|
С |
|
|
|
q=3Н/м |
|
м |
|
|
|
|
|
2 |
|
А |
|
2м |
М=2Нм |
В |
|
|
|
|
|||
|
|
|
6м |
|
|
|
y |
|
P |
P sin 60 |
o |
|
|
|
|
||
|
YA |
|
60 0 |
С |
|
|
|
P cos 60o |
|
|
|
|
|
|
|
2м |
|
A |
|
|
|
x |
|
|
X A |
Q |
M |
B |
|
M A |
|
|
|
||
1м |
|
|
|
||
|
|
|
|
||
|
2м |
|
|
|
|
|
|
|
6м |
|
|
|
|
|
Рис. 1.1 |
|
|
Решение. Рассмотрим равновесие угольника АВС. Изобразим его в свободном состоянии, т.е. покажем действующие на него силы P
и Q , пару сил с моментом М и реакции связи X A , YA , M A . Так как
угольник находится в равновесии под действием произвольной плоской системы сил, то уравнения равновесия угольника запишем в виде:
Fx 0; Fy 0; mAAF 0 .
5
Fx |
0 : X A P cos60 0 ; |
(1) |
||
Fy |
0 : YA Q Psin 60 0 ; |
(2) |
||
|
|
|
|
|
mA F |
0 : M A Q 1 M Psin 60 6 |
|
||
|
|
|
Ðcos60 2 0 . |
(3) |
Из (1) ХА P cos60 2 12 1 Н.
Из (2) YA Q Psin 60 6 2 0,866 7,73 Н.
Здесь Q q 2 3 2 6 кН.
Из (3) M A Q 1 M Psin 60 6 Ðcos60 2 20,38 Нм.
Проверка.
|
|
|
|
mÑ F |
0 : M A YA 6 X A 2 Q 5 M 0 . |
(4) |
|
Подставляя в уравнение (4) найденные ХА, YA, МА, получаем:
20,38 7,73 6 2 6 5 2 0 ; 0 0 .
Значит, задача решена верно.
Ответ: X A 1 Í ; YA 7,73 Í ; M A 20,38 Í ì .
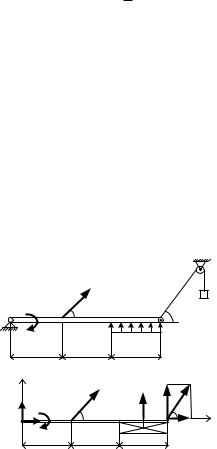
Пример 1.2. Определить реакцию шарнира А и вес груза Р, удерживающего балку АВ в равновесии (рис. 1.2).
|
F = 2 н |
P |
|
|
|
A |
450 |
|
|
|
|
M |
C |
B |
|
|
q = 2 н/м |
2 м |
2 м |
2 м |
y |
|
|
|
Psin600 |
|
|
F = 2 н |
Q |
|
|
|
|
|
P |
|
||
|
|
|
|
||
YA |
|
450 |
|
600 |
x |
|
M |
|
|
Pcos600 |
|
XA |
|
|
|
||
2 м |
2 м |
2 м |
|
||
Рис. 1.2
6

Решение. Рассмотрим равновесие балки АВ. В свободном
состоянии на нее действуют силы F; P; Q , пара сил с моментом
М = 40 Нм, равномерно распределенная нагрузка интенсивностью q = 2 Н/м и реакция шарнирно-неподвижной опоры А, которую
заменяем силами X A и YA . Равномерно распределенную нагрузку заменим сосредоточенной силой Q q 2 4 Í . Так как балка
АВ находится в равновесии под действием произвольной плоской системы сил, то запишем ее уравнения равновесия в виде:
Fx 0; Fy 0; mAF 0 .
Оси координат выберем, как показано на чертеже.
Fx |
0 : X A F cos 45 Pcos60 0 ; |
(1) |
||
Fy |
0 : YA F sin 45 Q Psin 60 0 ; |
(2) |
||
|
|
|
|
|
mA F |
0 : M F sin 45 2 Q 5 Psin 60 6 0 . |
(3) |
||
Из (3) получаем:
Ð |
M F sin 45 2 Q 5 |
|
40 2 0,707 2 20 |
3,3 Í . |
||
sin 60 6 |
|
0,866 6 |
||||
|
|
|
||||
Из (1) следует: |
|
|
|
|||
X A F cos 45 Pcos60 2 0,707 3,3 0,5 3,06 Í .
Из (2) имеем:
YA F sin 45 Q Psin 60 2 0,707 4 3,3 0,866 8, 27 Í .
Проверка.
mÑ F 0 : YA 2 Ì Q 3 Ðsin 60 4 0 ,
( 8, 27 2) 40 4 3 3,3 0,866 4 0 ,
0,01 0 0 .
Задача решена верно.
Ответ: P = 3,3 Н; ХА = – 3,06 Н; YA = – 8,27 H.
7
Задача № 2 посвящена определению положения центра тяжести однородной плоской фигуры.
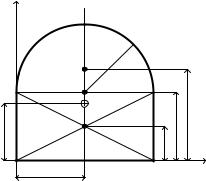
Пример 1.3. Определить координаты õÑ и óÑ центра тяжести однородной пластины (рис. 1.3).
yC = 1,81 м
y |
|
O2 |
|
R=2м |
|
C2 |
|
O3 |
|
C |
|
м |
2 |
2 |
y |
C1 |
|
1 |
|
y |
|
x1 = x2 = xC = 2 м O1 |
x |
Рис. 1.3
Решение. Применим метод разбиения. Разобьем фигуру на прямоугольник (1) и полукруг (2). Так как пластина симметрична относительно оси О1О2, то хС = 2 м.
y |
S1 y1 S2 y2 |
, |
|
|
|||
Ñ |
S1 |
S2 |
|
|
|
||
где площадь прямоугольника S1 = 4 2 8 м2; площадь полукруга
S2 |
= |
R2 |
2 м2; у1 = 1 м; |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
R sin |
2 |
8 |
|
|||
|
|
y2 |
Î |
1Î 3 |
Î 3Ñ2 2 |
2 |
|
2 |
|
2,84 м. |
|||||
|
|
|
|
|
|
|
|||||||||
|
|
3 |
|
|
|
|
3,14 |
||||||||
|
|
|
|
|
|
|
|
3 |
|
||||||
|
Тогда |
y |
|
8 1 2 2,84 |
1,81 м. |
|
|
||||||||
|
|
|
|
||||||||||||
|
|
|
Ñ |
|
|
8 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: хС = 2 м; yÑ 1,81 м.
8
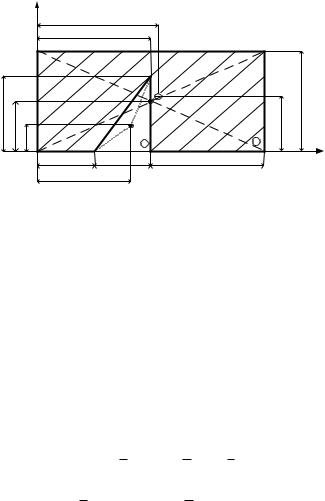
Пример 1.4. Определить положение центра тяжести однород- |
|||||||
ной пластины ABCDEFK (рис. 1.4). |
|
|
|
||||
|
y |
|
|
|
|
|
|
|
|
xc |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
B |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
C |
|
|
|
3м |
|
|
|
C1 |
|
|
4м |
|
|
|
|
|
|
||
1 |
|
|
|
C2 |
|
c |
|
y |
|
|
|
|
y |
|
|
2 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
A |
2м |
K |
2м |
E |
4м |
D |
x |
|
x2 |
|
|
|
|||
Рис. 1.4
Решение. Применим метод отрицательных площадей. Дополним фигуру треугольником KEF, считая его площадь отрицательной.
Тогда
õ |
|
S1õ1 S2 õ2 |
|
32 4 3 3,33 |
4,069 ì ; |
||||||
|
|
|
|
|
|||||||
Ñ |
|
|
|
S1 S2 |
|
|
|
32 3 |
|||
|
|
|
|
|
|
|
|||||
y |
|
|
S1 y1 |
S2 y2 |
|
32 2 3 1 |
2,103 ì , |
||||
|
|
|
|
|
|||||||
Ñ |
|
|
S1 |
S2 |
|
|
|
32 3 |
|||
|
|
|
|
|
|
|
|||||
где
x1 4 ì ; ó1 2 ì ; S1 32 ì 2 ; x2 2 23 ÊÅ 2 23 2 3 13 ì ;
ó2 13 3 1 ì ; S2 12 2 3 3 ì 2 . Ответ: õÑ 4,069 ì ; yÑ 2,103 ì .
9
|
|
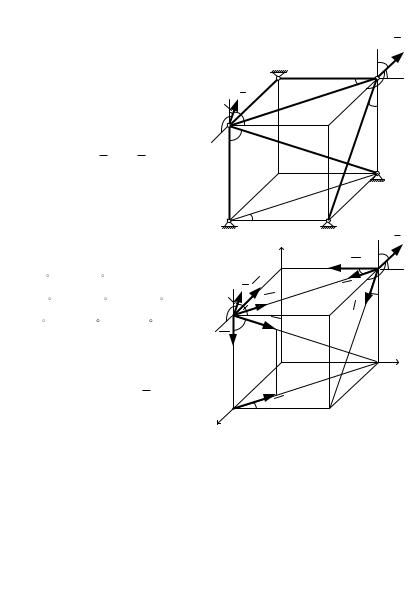
Задача С3 посвящена определению усилий в стержнях про- |
|||||||||||||||
странственной конструкции. |
|
|
|
|
|
|
|
||||||||||
|
|
Пример 1.5. |
Конструкция |
|
|
|
|
|
|
P |
|||||||
состоит из невесомых стерж- |
|
|
|
|
|
1 |
|
||||||||||
ней 1, 2, …, 6, |
соединенных |
|
|
A |
1 |
ψ |
K |
β1 |
|||||||||
|
|
|
α1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
друг с другом (в узлах К и М) |
|
|
|
|
|
||||||||||||
Q |
4 |
|
2 |
|
|
|
|||||||||||
и |
|
с неподвижными |
|
опорами |
2 |
|
|
|
|
φ |
|
||||||
|
|
α2 |
β2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А, |
В, |
С, |
D |
шарнирами |
M |
|
|
|
|
|
|
||||||
(рис. 1.5). В узлах К и М при- |
δ |
|
|
5 |
3 |
|
|
||||||||||
ложены силы P и |
Q , |
обра- |
6 |
|
|
|
|
D |
|
||||||||
зующие |
с |
координатными |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
осями углы |
1 , |
1 , |
|
1 |
и 2 , |
|
ψ |
|
|
|
|
|
|||||
2 , 2 соответственно. |
|
B |
|
|
C |
|
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
Определить усилия в стерж- |
|
|
z |
|
|
1 |
P |
||||||||
нях 1–6, если дано: Р = 100 Н, |
|
|
A |
1 |
N1 |
K |
β1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
|
|
|
1 |
60 , 1 60 |
, Q 50H, |
|
|
4 |
|
α1 |
||||||||||
|
|
|
|
||||||||||||||
Q |
|
|
2 |
N2 |
φ |
|
|||||||||||
|
|
45 , |
|
60 , |
|
60 ; |
2 |
|
N2 |
|
|
|
|
||||
|
|
|
α2 |
β2 |
|
N |
3 |
|
|||||||||
2 |
2 |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
||||
30 , 60 , 74 . |
|
N |
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
δ |
|
5 |
|
|
|
|
|||||||||||
|
|
5 |
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Решение. |
Рассмотрим рав- |
N6 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
новесие узла К, в |
|
котором |
6 |
|
|
|
|
D |
y |
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||
сходятся стержни 1, |
|
2, |
3. На |
|
|
|
|
|
|
|
|||||||
узел действуют сила |
|
P |
и ре- |
|
ψ |
1 |
|
|
|
|
|||||||
|
B |
N5 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
акции |
стержней, |
|
|
которые |
|
|
|
|
C |
|
|
||||||
|
|
x |
|
|
|
|
|
|
|||||||||
направим по стержням от узла, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
считая стержни растянутыми. |
|
|
|
Рис. 1.5 |
|
|
|
||||||||||
Составим уравнения равнове- |
|
|
|
|
|
|
|
||||||||||
сия полученной пространственной системы сходящихся сил: |
|
||||||||||||||||
|
|
Fkx |
0 : Pcos 1 N2 sin N3 sin 0 ; |
|
|
(1) |
|||||||||||
|
|
Fky |
0 : Pcos 1 |
N1 N2 cos 0 ; |
|
|
|
|
(2) |
||||||||
|
|
Fkz |
0 : Pcos 1 |
N3 cos 0 . |
|
|
|
|
|
(3) |
|||||||
|
|
Решив уравнения (1), (2), (3) при заданных числовых значени- |
|||||||||||||||
ях силы Р и углов, получим N1 = 349 H, N2 = –345 H, N3 = 141 H. |
|||||||||||||||||
10

Рассмотрим равновесие узла М. На узел действуют сила Q и реакции N2 , N4 , N5 , N6 , стержней. Составим уравнения равновесия:
Fkx |
0 : Qcos 2 N2 sin N4 N5 sin sin 0 ; |
(4) |
|
Fky |
0 : Qcos 2 |
N2 cos N5 sin cos 0 ; |
(5) |
Fkz |
0 : Qcos 2 |
N5 cos N6 0 . |
(6) |
При определении проекций силы N5 на оси х и у в уравнени-
ях (4) и (5) удобнее сначала найти проекцию |
|
|
|
||
|
|
||||
N5 этой силы на |
|||||
плоскость |
хОу (по |
|
|
|
|
числовой величине N5 N5 sin ), а затем |
|||||
найденную проекцию на плоскость спроецировать на оси х, у. |
|||||
Решив |
систему |
уравнений (4), (5), (6), |
|
|
учитывая, что |
N2 345 H , найдем значения N 4, N 5, N 6.
Ответ: N 1 = 349 H, N 2 = –345 H, N 3 = 141 H, N 4 = 50 H, N5 = = 329 H, N 6 = –66 H. Знак «минус» показывает, что стержни 2 и
6 сжаты, остальные — растянуты.
Задача С4 посвящена определению реакций опор тела, находящегося в равновесии под действием произвольной пространственной системы сил.
Пример 1.6. Горизонтальная прямоугольная однородная плита весом Р закреплена сферическим шарниром в точке А, цилиндрическим шарниром (или подшипником) в точке В и невесомым стержнем DD (рис. 1.6). На плиту в плоскости, параллельной xz, действует сила F , а в плоскости, параллельной zy, — пара сил с моментом M.
Определить реакции опор А и В и стержня DD , если Р = 3 кН,
F = 8 кН, М = 4 кНм, = 60 , АС = 0,8 м, АВ = 1,2 м, ВЕ = 0,4 м, ЕН = 0,4 м.
Решение. Рассмотрим равновесие плиты. В свободном состоя-
нии на плиту действуют заданные силы P , F и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира
разложим на три составляющие: X A , YA , ZA , — а цилиндрического (подшипника) — на две составляющие: X B , ZB (в плоскости, пер-
11
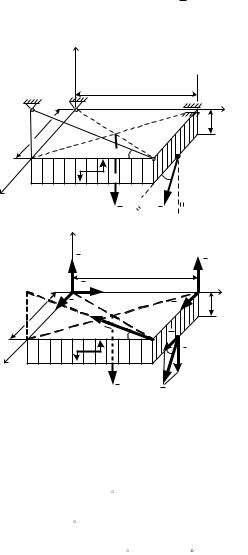
пендикулярной оси подшипника); реакцию N стержня направляем вдоль стержня от D к D1, предполагая, что он растянут.
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 м |
|
|
|
|
|
A |
|
|
|
|
|
|
B |
y |
|
|
|
|
|
|
|
|
|
|
0.4м |
|
D1 |
8м |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
30 |
0 |
|
D |
|
H |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
z |
|
|
|
|
P |
|
|
|
F |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
z |
|
|
|
|
|
|
|
|
|
|
Z A |
|
|
|
|
|
|
ZB |
|
|
|
|
|
|
|
1.2 м |
|
|
|
|
|
A |
YA |
|
|
|
|
|
|
B |
y |
|
|
|
|
|
|
|
|
|
0.4м |
|
|
8м |
X A |
|
|
|
|
|
X B |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
C |
N |
30 |
0 |
|
D |
F |
H |
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
M |
|
|
|
|
|
|
F |
|
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.6 |
|
|
|
|
||||
Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
Fkx 0 : |
X A X B F cos60 |
0 ; |
|
(1) |
||
Fky |
0 : |
YA N cos30 0 ; |
|
|
|
(2) |
Fkz |
0 : |
ZA ZB P N sin 30 |
F sin 60 |
0 ; |
(3) |
|
12
