
Metod (2529)
.pdf
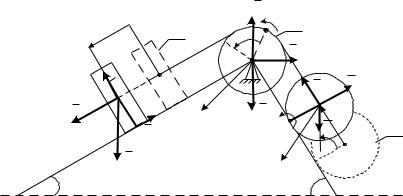
Решение. Рассмотрим движение точки В как сложное, считая ее движение по прямой AD относительным, а вращение пластины — переносным. Тогда абсолютная скорость и абсолютное ускорение найдутся по формулам:
|
|
àáñ î òí ï åð ; |
(1) |
||||||
|
|
àáñ |
|
|
|
|
|
|
(2) |
a |
aî òí aï åð aêî ð , |
||||||||
где, в свою очередь, aî òí aî òí , так как относительное движение
прямолинейное, и aînòí 0 ; aï åð aï åð aïnåð .
Определим модули всех входящих в равенства (1) и (2) векторов.
1. Относительное движение. Уравнение относительного движения
s AB 2 15t 3t 2 .
Поэтому
î òí |
|
|
s |
|
|
|
15 6t |
|
t 2 c |
|
15 12 |
|
3 м/с, |
||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
a |
|
|
|
|
s |
|
6 |
6 см/с2. |
||||||||||
|
î òí |
|
î òí |
|
|
|
|
|
|
|
|
|
|
|
|||||
В момент времени t1 = 2 c имеем:
s AB |
20 см, |
|
3 |
см/с, a |
|
6 см/с2. |
(3) |
|
1 |
1 |
|
î òí |
|
î òí |
|
|
|
Знаки s и s показывают, что вектор î òí |
направлен в сторону |
|||||||
положительного отсчета АВ, а вектор aî òí — в противоположную
сторону. Изображаем все эти векторы на рис. 2.4.
2. Переносное движение. Уравнение переносного движения
пер = (0,1t3 – 2,2t) рад.
Найдем угловую скорость ï åð и угловое ускорение пер переносного вращения:
|
|
|
|
|
|
0,3t2 |
2,2 |
|
|
|
1 |
|
1 c 1 ; |
||||
|
|
|
|
|
|||||||||||||
ï åð |
|
|
ï åð |
|
|
|
|
|
|
t 2 c |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1, 2 c 2 . |
||||||||
|
ï åð |
|
|
|
|
|
0,6t |
t 2 c |
|||||||||
|
|
ï åð |
|
|
ï åð |
|
|
|
|
|
|
||||||
23

Знаки ï åð è ï åð указывают, что в момент t1 = 2 c направление дуги ï åð совпадает с направлением положительного отсчета углаï åð , а направление дуги ï åð ему противоположно. Отметим это
на рис. 2.4 соответствующими дуговыми стрелками. Из рисунка находим расстояние h1 точки В1 от оси вращения z:
h1 = AB1 sin30 = 10 см.
Тогда в момент t1 = 2 c, учитывая равенства (4), получим:
|
|
|
|
|
|
|
ï åð ï åðh1 10 см/с; |
|
|||||||
a |
|
|
ï åð |
h 12 см/с2; an |
|
2 |
h 10 см/с2, |
(5) |
|||||||
ï åð |
|
1 |
|
|
ï åð |
|
ï åð 1 |
|
|
|
|||||
Векторы |
|
|
и |
|
|
|
|
направлены перпендикулярно плоскости |
|||||||
ï åð |
à |
|
|||||||||||||
|
|
|
ï åð |
|
|
|
|
|
|
|
|
||||
ADE в соответствии с дугами |
и |
|
|
, а вектор |
|
n |
— по ли- |
||||||||
ï åð |
à |
||||||||||||||
|
|
|
|
|
|
|
|
ï åð |
|
|
ï åð |
|
|||
нии В1С к оси вращения, перпендикулярно |
|
|
. Изобразим их на |
||||||||
à |
|||||||||||
|
|
|
|
|
|
|
ï åð |
|
|
||
рис. 2.4. |
|
|
|
|
|
|
|
|
|
||
3. Кориолисово ускорение. Так как угол между вектором î òí |
|||||||||||
и осью вращения (вектором |
|
) равен 30 , то численно в мо- |
|||||||||
|
|
|
|
ï åð |
|
|
|
|
|
|
|
мент времени t1 = 2 c |
|
|
|
|
|
|
|
|
|
||
|
a |
2 |
|
sin 30 |
3 см/с2 |
. |
(6) |
||||
êî ð |
î òí |
ï åð |
|
|
|
|
|
|
|
||
Направление |
|
êî ð |
определим |
по |
правилу |
Н.Е. Жуковского. |
|||||
à |
|||||||||||
Для этого вектор î òí спроецируем на плоскость, |
перпендику- |
||||||||||
лярную оси вращения, и затем эту проекцию повернем на 90° в соответствии с ï åð , т.е. по ходу часовой стрелки. Получим
направление вектора àêî ð : он направлен перпендикулярно плос-
кости пластины, так же, как вектор ï åð |
(см. рис. 2.4). |
|||||||
4. Определение абсолютной скорости абс. |
||||||||
Так как î òí |
ï åð , то |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
62 102 |
|
10, 44 см/с. |
àáñ |
|
î òí |
ï åð |
|
|
|
|
|
24
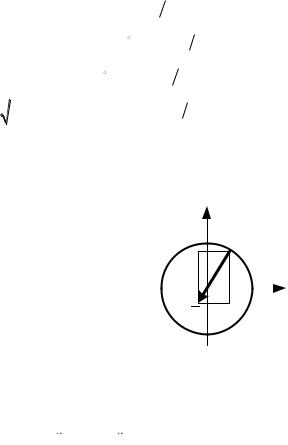
5. Определение абсолютного ускорения аабс.
Так как составляющие вектора абсолютного ускорения не расположены в одной плоскости, то выберем прямоугольную пространственную систему координат В1, х, у, z и спроецируем на эти оси равенство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
à |
|
|
à |
à |
a |
||||||||||||||||||||||||||
|
|
àáñ |
|
|
î òí |
|
|
ï åð |
|
ï åð |
êî ð |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a à |
|
à |
|
9 ñì ñ2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
àáñ |
|
|
|
|
ï åð |
|
|
êî ð |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
õ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
à |
àï |
|
à |
|
sin30 13 ñì ñ2 ; |
||||||||||||||||||||||||||||
|
àáñó |
|
|
|
ï åð |
|
|
|
|
î òí |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
à à |
|
|
|
cos30 |
5, 20 ñì |
ñ2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
àáñ |
|
î òí |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Отсюда à |
|
à2 |
|
à2 |
|
|
à2 |
|
16, 64 ñì |
ñ2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
àáñ |
|
àáñ |
|
àáñ |
ó |
|
|
àáñ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
õ |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
= 10,44 см/с; |
a |
|
= 16,64 см/с2. |
||||||||||||||||||||||||||||||
àáñ |
|
|
|
|
|
|
|
|
|
|
|
àáñ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ, |
|||||||||||||||||||||||||||||||||
ВХОДЯЩИХ В КОНТРОЛЬНУЮ РАБОТУ № 3 |
||||||||||||||||||||||||||||||||||
Пример 3.1 (прямая задача). Урав- |
|
|
|
|
|
y |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
нения движения материальной точки |
|
|
|
|
|
Rx = -0, 82 м |
||||||||||||||||||||||||||||
массой m = 2 кг: х = 3 sin t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
м; |
|
|
|
|
|
|
|
|
|
|
(1,5; 2,6) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ry = -1,42 м |
|||||||||
у = 3 cos t м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
||||||||||||
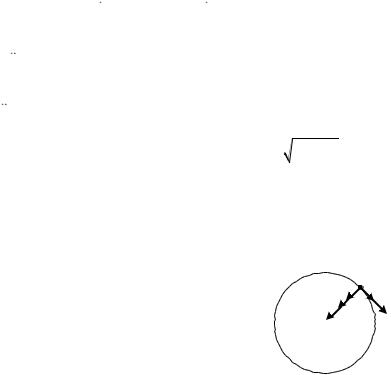
Определить равнодействующую R сил, действующих на эту точку в момент времени t1 = 1 c.
Решение. Движение точки задано координатным способом (рис. 3.1).
Запишем дифференциальные уравнения движения точки: m x Rx ; m y Ry ,
25
где m — масса точки, x и y — проекции вектора ускорения a
на оси координат, Rx и Ry — проекции равнодействующей сил, действующих на точку, на эти же оси.
Очевидно:
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
y |
3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
cos |
|
t |
, |
|
|
sin |
t ; |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|||
|
|
3 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
|
sin |
|
|
t |
|
|
|
sin |
|
t |
|
t1 1 c |
|
|
0,5 0, 41 м/с |
; |
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
36 |
|
6 |
|
|
|
|
12 |
|
|
6 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||||||
|
3 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
y |
|
|
cos |
|
t |
|
|
|
cos |
|
|
t |
|
|
t1 1 c |
|
|
|
0,866 0,71 м/с |
. |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
36 |
|
|
6 |
|
|
|
12 |
|
|
6 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Тогда Rx|t = 1c |
= –0,82 H; Ry|t |
= 1c = –1,42 H; R = |
|
R2 |
R2 |
1,64 H . |
||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
Траекторией движения точки является окружность, описанная уравнением:
х2 + у2 = 32,
х|t = 1c = 3 0,5 1,5 м, у|t = 1c = 3 0,866 2,598м. |
|
|
|
|
||||
Ответ: R = 1,64 Н. |
|
|
|
|
|
|
|
|
Пример 3.2 (прямая задача). Материаль- |
|
|
|
M |
|
|
|
|
ная точка массой m = 2 кг движется по |
|
|
|
n |
|
|
|
|
окружности радиуса r = 3 м с постоянной |
|
|
|
|
|
|
||
|
|
an |
|
|
||||
|
|
|
|
|
|
|||
скоростью = 2 м/с. |
|
|
|
|
|
|
|
|
R |
Rn |
|
|
|
|
|||
Определить равнодействующую R сил, |
|
|
|
|
|
|
|
|
действующих на эту точку.
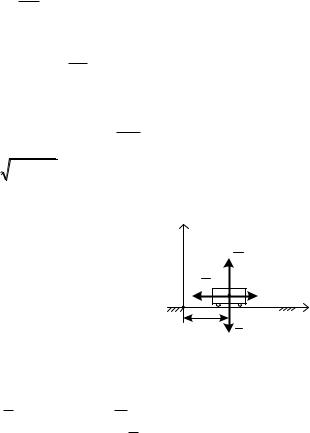
Решение. Движение точки задано есте- |
Рис. 3.2 |
|
ственным способом, так как траектория ее |
||
|
движения задана (рис. 3.2).
Запишем дифференциальные уравнения движения точки в естественной форме:
ma R ; man Rn ; mab Rb , |
(1) |
26
где m — масса точки, a , an , ab |
— проекции вектора ускорения |
|||||||||||||||
точки на естественные оси координат. R , Rn , Rb |
— проекции |
|||||||||||||||
равнодействующей сил на эти оси. В нашем случае используют- |
||||||||||||||||
ся только два первых уравнения, так как точка движется в плос- |
||||||||||||||||
кости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как a |
|
|
d |
, а |
a |
2 |
1,33 м/с2, то уравнения (1) мож- |
|||||||||
|
|
dt |
|
|
n |
|
r |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
но записать в следующем виде: |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
m |
d |
R |
|
; |
m |
2 |
R . |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
r |
n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как const , то a 0 и R |
0 , а |
|
||||||||||||||
|
|
|
|
|
R m 2 |
|
|
2 4 2,67 H . |
|
|||||||
|
|
|
|
|
n |
|
|
r |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда R |
|
R2 |
R2 |
2,67 H . |
|
|
|
|
||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Ответ: R 2,67 H . |
|
|
|
|
|
|
|
|
|
|||||||
Пример |
3.3 |
|
(обратная |
|
задача). |
y |
|
|||||||||
Груженый железнодорожный |
вагон |
|
||||||||||||||
|
|
|||||||||||||||
общей массой 80 т движется равно- |
|
|
||||||||||||||
мерно со скоростью 0 |
= 2 м/с по |
N |
|
|||||||||||||
горизонтальным рельсам. Затем его |
R |
|
||||||||||||||
движение затормаживается. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
O |
|
|||||||||
Определить |
расстояние, |
которое |
x |
x |
||||||||||||
пройдет вагон к тому моменту, ко- |
P |
|
||||||||||||||
гда его скорость уменьшится в 2 ра- |
|
|||||||||||||||
Рис. 3.3 |
||||||||||||||||
за, если сила сопротивления движе- |
||||||||||||||||
|
|
|||||||||||||||
нию постоянна и равна 2 кН. |
|
|
|
|
|
|
|
|||||||||
Решение. Покажем силы, действующие на вагон во время |
||||||||||||||||
торможения: P — вес вагона; N — суммарная нормальная ре- |
||||||||||||||||
акция рельсов на колеса вагона; R — сила сопротивления дви- |
||||||||||||||||
жению (рис. 3.3). |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
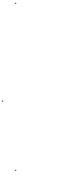
II закон Ньютона:
|
|
|
|
|
|
|
|
|
|
|
|
ma R N P . |
|
|
(1) |
||||||||
Проецируем (1) на х: |
|
|
|
||||||||
m x R или x |
R |
. |
(2) |
||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
(2) — дифференциальное уравнение движения вагона во время торможения. Проинтегрируем его дважды:
x |
R |
t C ; |
|
(3) |
||||
|
|
|||||||
|
|
|
|
m |
1 |
|
|
|
|
|
|
|
|
|
|
||
x |
R |
|
t2 |
C t C . |
(4). |
|||
|
|
|||||||
|
m 2 |
|
1 |
2 |
|
|||
|
|
|
|
|
||||
Определим постоянные интегрирования С1 и С2 из начальных условий: t0 0 ; x0 0 ; x0 0 . Подставляя начальные условия в
(3) и (4), получим C1 0 ; C2 0 . Тогда
x |
R |
t ; |
(5) |
||
|
|||||
|
|
m |
0 |
|
|
|
|
|
|
||
x |
Rt2 |
t . |
(6) |
||
|
|||||
|
2m |
0 |
|
||
|
|
|
|||
Найдем время, за которое скорость вагона уменьшится в 2 раза.
Из (5): 0 |
|
R |
t |
|
. Отсюда t |
0 |
m |
|
2 80 |
40 с. |
||||||
2 |
|
m |
1 |
0 |
|
1 |
2 R |
|
2 2 |
|
||||||
Тогда из (6) искомое расстояние |
|
|
|
|
|
|
||||||||||
|
|
|
|
R t2 |
|
2 402 |
|
|
|
|||||||
s x(t ) |
|
|
|
1 |
t |
|
|
2 40 20 80 60 м. |
||||||||
|
|
|
|
|
||||||||||||
|
1 |
|
|
m 2 |
0 1 |
80 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
Ответ: s = 60 м.
Задача № 3 на применение теоремы об изменении кинетической энергии механической системы к исследованию движения различных механизмов.
28
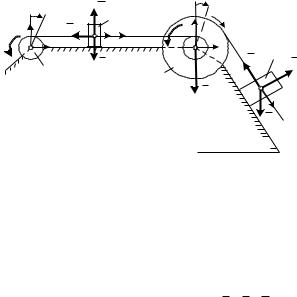
Пример 3.4. Механическая система, состоящая из двух однородных дисков 2 и 3 и груза 1, связанных между собой нерастяжимой нитью, приводится в движение из состояния покоя.
Определить скорость груза 1, когда он пройдет путь s1 = 0,2 м, если заданы массы: m1 ; m2 0,5m1 ; m3 0,2m1 . Коэффициент
трения f груза о шероховатую наклонную поверхность равен 0,1 (рис. 3.4).
|
|
s |
YO2 2 |
|
|
|
s1 |
1 |
2 |
2 |
|
|
1 |
|
|||
|
|
|
|
||
|
|
O2 |
X O2 |
|
|
|
N1 |
|
|
|
N3 |
|
|
|
|
O3 |
|
1 |
|
z |
P2 3 |
O3 |
|
|
|
|
|
|
s |
|
|
|
|
|
1 |
|
|
FТР1 |
P |
|
P3 |
|
|
|
|
zO |
3 |
|
P |
|
|
|
|
|
1 |
|
|
3 |
|
300 |
|
|
|
600 |
|
Рис. 3.4
3
Решение. Запишем теорему об изменении кинетической энергии механической системы в интегральной форме:
T – T0 = Ae + i, |
(1) |
где Т0 — кинетическая энергия механической системы в начальный момент времени, а Т — в момент времени, когда груз 1 переместится на s1; Ae + i — работа внешних (е) и внутренних (i) сил механической системы на совокупности перемещений ее элементов (1, 2, 3).
Так как механическая система в начальный момент времени была в покое, то Т0 = 0. Вычислим
Т = Т1 + Т2 + Т3,
где Т1, Т2, Т3 — кинетическая энергия груза и дисков соответственно.
29
|
m 2 |
|
||
Т1(движется поступательно) = |
1 |
1 |
; |
|
2 |
|
|
||
|
|
|
|
|
Т2(вращается вокруг точки О2) = |
J z |
2 |
, |
|
2 |
||||
|
|
2 |
|
|
где Jz — момент инерции однородного диска 2 относительно оси z, проходящей через точку О2 перпендикулярно плоскости диска,2 — угловая скорость вращения диска:
|
|
|
|
|
|
|
|
|
|
m R2 |
; |
|
|
||||
|
|
|
|
|
J |
|
|
2 2 |
|
1 |
. |
||||||
|
|
|
|
|
|
|
z |
|
|
2 |
|
|
2 |
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда T |
m2 R22 |
|
12 |
1 |
|
|
m2 12 |
. |
|
|
|
|
|||||
|
|
R2 |
|
|
|
|
|
|
|
|
|||||||
2 |
2 |
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m3 O2 |
JZ |
|
2 |
|
|||
Т3 (плоское движение) = |
3 |
|
|
3 |
— формула Кенига, так |
||||||||||||
2 |
|
|
Î 3 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
как всякое плоское движение есть сумма его поступательного движения вместе с полюсом С3 и вращательного движения вокруг оси zO3 , проходящей через полюс перпендикулярно плоскости диска.
|
|
|
|
(одна нить); |
|
O |
|
|
|
|
|
|
|
|
|
m R2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
1 |
; J |
|
|
|
|
|
3 3 |
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
O |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
R3 |
|
|
R3 |
|
|
|
2 |
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Î |
3 |
|
|
|
|
||||||||
|
|
|
T |
m 2 |
|
m R2 |
|
2 |
1 |
|
3 |
m 2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Значит, |
|
3 |
1 |
|
3 3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
R2 |
2 |
|
|
4 |
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 2 |
|
m |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Т = |
|
1 |
1 |
|
|
2 |
1 |
|
|
|
|
|
m 2 |
|
|
|
|
|
(m |
0,5m |
|
|
1,5m ) 2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
4 |
|
|
|
|
4 |
|
3 |
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
3 |
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
(m |
|
|
1 |
m 0,3m ) 2 |
0,78m |
2 . |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
4 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Работа внутренних сил (сил взаимодействия между элементами системы) равна нулю, т.е. Ai = 0.
30

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Внешними |
силами системы |
являются: P, N , F |
, P , X |
, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
òð1 |
2 |
|
Î 2 |
||||||||
YO |
, N2 , N3 , P3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Работа сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равна нулю, |
так как силы |
|||||||||||||||||
|
|
|
N1, N2 |
, N3 , P2 |
, XO |
, YO |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
N1, N3 , перпендикулярны перемещениям точек их приложения,
а силы N2 , P2 , XO2 , YO2 приложены к неподвижным точкам.
A |
PS sin 30 ; |
A |
|
P fS cos30 ; |
A |
P S sin 60o . |
P |
1 1 |
F |
|
1 1 |
P |
3 1 |
1 |
|
ÒÐ |
|
3 |
|
|
|
|
|
1 |
|
|
|
Тогда |
|
|
|
|
|
|
Ae i P S |
sin 30o P fS |
1 |
cos 30o P S sin 60o = |
||
1 |
1 |
1 |
3 |
1 |
|
= (m1 0,5 m1 0,1 0,866 0,2m1 0,866)gS1
(0,5 0,66 0,173)m1gS1 4,1m1 .
Подставляя Т и Ae i в равенство (1), получим:
|
|
|
|
0,78m 2 |
4,71m . |
|
|
|
1 |
1 |
1 |
||
|
|
|
|
|
||
Отсюда |
4,71 |
|
2, 46 м/с. |
|||
|
||||||
1 |
|
0,78 |
|
|
|
|
|
|
|
|
|
|
|
Ответ: 1 2, 46 м/с.
Пример 3.5. Механическая система (рис. 3.5) состоит из обмотанных нитями блока 1 радиуса R1 и ступенчатого шкива 2 (радиусы ступеней R2 и r2, радиус инерции шкива относительно оси вращения ρ2), а также из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенных к блоку 1.
Определить ускорение а3 груза 3, пренебрегая трением, если
дано: P1 = 0, Р2 = 30 Н, Р3 = 40 Н, Р4 = 20 Н, М = 16 Н∙м, R1 = 0,2 м,
R2 = 0,3 м, r2 = 0,15 м, ρ2 = 0,2 м.
Решение. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, — идеальные.
31
|
|
N4 |
|
|
|
|
2 |
|
|
|
1 |
|
|
y |
2 |
2 |
|
|
|
4 |
|
|
|
|
|
||||
y1 |
|
|
|
|
|
|
|
|
|
и |
s4 |
а4 |
М |
и |
|
|
|
|
|
М |
F4 |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
и |
3 |
|
1 |
Р4 |
|
|
|
|
|
F3 |
N3 |
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Р2 |
s 3 |
|
Р3  а3
а3
600 
Рис. 3.5
Для определения ускорения а3 груза 3 применим общее уравнение динамики:
|
Akà Akè 0 , |
(1) |
где Akà |
— сумма элементарных работ активных сил; Akè |
— |
сумма элементарных работ сил инерции. |
|
|
Изображаем на чертеже активные силы P2 , P3 , P4 и пару сил с моментом М. Задавшись направлением ускорения a3 , показыва-
|
|
|
|
|
|
и |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ем на чертеже силы инерции F 3 , |
|
F 4 и пару сил инерции с мо- |
||||||||||||
ментом M и , величины которых равны: |
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F è m a ; |
F è |
m a ; |
M è m 2 |
2 |
. |
(2) |
||||||||
3 |
3 |
3 |
4 |
4 |
4 |
2 |
2 |
2 |
|
|
||||
Сообщим системе возможное перемещение и составим общее уравнение динамики (1):
P3 sin 600 F3è s3 M2è 2 |
F4è s4 |
M 1 0 , |
(3) |
|||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
s |
R |
; s |
r |
|
; |
|
r2 |
|
|
. |
(4) |
|
2 |
|
|
2 |
|||||||||
3 |
2 |
2 |
4 |
2 |
1 |
|
R1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя величины (2) и (4) в уравнение (3), приведем его к виду
32
