пониманию необходимости введения новых чисел, т.е. к расширению понятия числа. С учащимися выясняется также такое свойство множества натуральных чисел, как бесконечность.

С помощью координатного луча сравниваются натуральные числа между собой, устанавливаются понятия «равно», «больше» и «меньше» для натураль­ных чисел. Важно, чтобы ученики усвоили такие понятия, как «числа, следую­щие за данным», «числа, предшествующие данному», умели ответить на вопро­сы: сколько чисел может непосредственно следовать за данным, сколько чисел может непосредственно предшествовать данному, кроме 1. На этом этапе дает­ся запись четного и нечетного чисел формулами: 2п, 2п + 1.

Особое внимание следует уделить действиям над многозначными числа­ми, трудным случаям умножения и деления, действиям с нулем и единицей и, в частности, «закону поглощения 0 (а + 0 = а, 0 + а = а)». Необходимо показать учащимся, что, например, действия 1 • а = а, 0 ■ а = 0 являются, по существу, следствиями из определения действия умножения, а а: 1 = а, а: а= 1,0 : а = О, а : К- из определения действия деления.

После изучения действий над натуральными числами можно рассмотреть с учениками вопрос о замкнутости множества натуральных чисел относительно сложения и умножения и отметить, что в отношении вычитания это свойство не выполняется.

Большое внимание в этой теме следует уделить законам арифметических действий (переместительному, сочетательному, распределительному). В учебни­ках математики они формулируются как свойства сложения и умножения. Важно показать глубокое теоретическое значение законов, так как у учащихся обычно создается впечатление, что законы нужны лишь для упрощения арифметических действий. В 5 классе законы арифметических действий записываются в общем ви­де с использованием буквенной символики. Рассмотрение коммутативного (пере­местительного) и ассоциативного (сочетательного) законов умножения целесооб­разно связать с геометрическим материалом, а именно с вычислением площадей прямоугольников и объемов прямоугольных параллелепипедов.

5. Основные вопросы методики изучения дробей

Второе расширение понятия числа, с которым встречаются учащиеся, за­ключается в присоединении к целым неотрицательным числам дробных поло­жительных чисел. На этом этапе следует добиться от них того, чтобы они четко различали понятия «дробь» и «дробное число». Для этого следует обратить внимание учащихся на то, что любое число х из множества дробных неотрица­тельных чисел может быть записано в виде дроби ,v где т eZ₀, п еN. Од-

п

2

по и то же число можно записать разными дробями. Гак, например, дроби 6 22

являются записями одного н того же числи.

9

12

8 24 7 23

Дроби -, — служат доя записи целых чисел, дроби - или — служат для 8 3 8 8

•записи дробных чисел. Таким образом, дробь может служить записью не только

дробного, но и целого числа.

Усвоению различия между дробными числами и дробью способствует вы- Iюлнение упражнений, аналогичных следующим:

1. Сколько содержится в записи 0,40; ^; 0,4; 0; ; 0,33; |: а) различ­ных чисел; б) дробных чисел; в) целых чисел?

3. х

2. Какое значение принимает х, если дроби - и — изображают одно и то же число?

Следует заметить, что в учебнике иногда происходит смешение понятий «дробь» и «дробное число». Так, в младших классах дробь трактуется как чис­ло, составленное из нескольких долей единицы. Значит, понятие дроби включа­ет в себя понятие дробного числа. Затем «дробь» используется для названия чи­сел из множества Q₀ и для названия записи такого числа. Когда говорят о дей­ствиях с дробями, то имеют в виду числа из О₀, когда же говорят о преобразо­вании дробей, то понимают записи чисел из go, так как нецелесообразно обра­щать одно число в другое. Поэтому с помощью специально подобранных во­просов необходимо приучать учащихся понимать из контекста, о чем идет речь: о числе или о его записи (символе).

Более четкого пояснения требует и понятие «десятичная дробь». При введении десятичных дробей основной акцент в учебнике (см., например, Ви­ленкин Н.Я. и др. Математика - 5, М., 2000) делается на то, что это дроби, ко­торые можно записать без знаменателя. Однако знаменатель у десятичной дро­би тоже записан, но по иному правилу.

Десятичные дроби изучаются рядом с натуральными числами. Это зако­номерно, так как действия с десятичными дробями во многом аналогичны дей­ствиям с натуральными числами, кроме того, имеется возможность использова­ния метрической системы мер, что облегчает изучение десятичных дробей. При >том сначала учащиеся знакомятся с обыкновенными дробями, изучают сложе­ние и вычитание дробей с одинаковыми знаменателями, сложение и вычитание смешанных чисел. Полученные знания помогают им в обосновании действий с десятичными дробями.

Изучение десятичных дробей в 5 классе осуществляется в такой последо­вательности: 1) десятичная запись дробных чисел; 2) сравнение десятичных дробей; 3) сложение и вычитание десятичных дробей; 4) приближенные значе­ния чисел, округление чисел; 5) умножение десятичных дробей на натураль­ные числа; 6) деление десятичных дробей на натуральные числа; 7) умно­жение десятичных дробей; 8) деление на десятичную дробь; 9) среднее арифме­тическое (см. Виленкин Н. Я. и др. Математика - 5, М., 2000).

Основное внимание при изучении десятичных дробей уделяется опера- типым умениям учащихся. В качестве примера рассмотрим методику изуче­нии сложения и вычитания десятичных дробей. Эти два действия в назван-

13

ном выше учебнике Н. Я. Виленкина изучаются одновременно (на одном уроке).

Учащимся предлагается сложить десятичные дроби 3,7 и 2,651. При этом сначала они уравнивают количество цифр после запятой, приписав к первой дроби два нуля справа: 3,7 = 3,700, потом записывают числа в смешанной фор­ме: 3,700 = 3 ™; 2,651 = 2-^-, после этого выполняют сложение: 3,7 + 2,651 1000 1000

, 700 , „ 651 ,700 + 651 . 1351 ,351 _с

- 3—— + 2 = 5 = 5—— = 6 = 6,351. Затем учащимся сооб-

1000 1000 1000 1000 1000 ³

щается, что тот же ответ можно получить иначе, сложив числа' 3,7 и 2,651

«столбиком» (приводится решение).

После этого находится разность тех же чисел:

3,7-2,651 =3— -2~- = 1 ⁷⁰⁰-~⁶⁵¹- = 1— = 1,049,

1000 1000 1000 1000

затем также сообщается, что ответ можно получить короче, вычитая числа

«столбиком» (приводится решение).

Правило формулируется одно для двух действий сразу:

«Чтобы сложить (вычесть) десятичные дроби, нужно:

1. уравнять в этих дробях количество знаков после запятой;

2. написать их друг под другом так, чтобы запятая была записана под чапятой;

3. выполнить сложение (вычитание), не обращая внимания на запятую;

1. поставить « ответе запятую под запятой в данных дробях».

< Vinci Inyr | и другой подход к изучению десятичных дробей. Авторы vieiiiiiiMin миIсмнгики для 5- 6 классов И.В. Баранова, З.Г. Борчугова предла- .'Ын, и I и питые чроОи после изучения обыкновенных дробей. Поэто-

1. "(ii.li I ц|ц)(\и у них и ручаются и 5 классе, а десятичные дроби - в 6

к '"ill научения материала в этом случае выглядит так:

2. и-* .и цопи кик ри чрядиыс единицы; 2) запись дробей с помощью деся-

ni'iin.is шпион, ччечии* десятичных дробей; 3) запись числа в виде десятичной и и ицж' оОыкноиешюН дроби; 4) сравнение десятичных дробей; 5) сложение десятичных дробей; 6) вычитание десятичных дробей; 7) округление чисел; К) совместное выполнение сложения и вычитания; 9) умножение десятичных дробей; 10) умножение десятичной дроби на 10, 100,1000 и т.д.; 11) деление де­сятичной дроби на натуральное число; 12) деление десятичной дроби на 10, 100, 1000 и т.д.; 13) деление на десятичную дробь; 14) среднее арифметиче­ское; 15) выполнение совместных действий над десятичными дробями; 16) вы­полнение совместных действий с обыкновенными и десятичными дробями.

Действия с десятичными дробями при таком подходе получают хорошее обоснование с помощью обыкновенных дробей. Рассмотрим этот момент под­робнее на примере изучения сложения десятичных дробей.

Учащимся предлагается задача: «Ученики 5-го А класса собрали 3,45 кг ли­пового цвета, а ученики 5-го Б класса - 4,23 кг. Сколько килограммов липового цвета собрали ученики 5-го А и 5-го Б классов?» Далее сообщается, что для ре­шения задачи нужно найти сумму чисел 3,45 и 4,23. Для этого дробные части этих чисел записывают в виде обыкновенных дробей и выполняют сложение:

14

100 100 100 100

Значит, 3,45 + 4,23 = 7,68. Итак, получаем ответ задачи: 7,68 кг.

После этого учащимся сообщается, что сумму 7,68 можно получить, если складывать числа 3,45 и 4,23 поразрядно, начиная с единиц низшего разряда: к 5 со тым прибавить 3 сотых, получим 8 сотых; к 4 десятым прибавить 2 десятых, по­лучим 6 десятых; к 3 единицам прибавить 4 единицы, получим 7 единиц.

После рассмотрения ещё одной аналогичной задачи вводится правило сложения двух десятичных дробей:

« Чтобы сложить две десятичные дроби, надо:

1. подписать слагаемые одно под другим так, чтобы цифры одинаковых разрядов были в одном столбце (тогда запятая окажется под запятой);

2. сложить числа поразрядно;

3. поставить в полученной сумме запятую под запятыми в слагаемых».

Далее сообщается, что сложение более двух десятичных дробей выполня­ется по этому же правилу. Если слагаемые имеют разное число десятичных пипсов, то, чтобы не допустить ошибки при записи одного слагаемого под дру­гим, можно уравнять число десятичных знаков. Для этого следует приписать к дроби, содержащей меньшее число десятичных знаков, справа нули.

Нахождение суммы десятичных дробей иллюстрируется на координатном луче. Справедливость переместительного и сочетательного законов сложения десятичных дробей обосновывается их справедливостью для обыкновенных дробей. Законы сложения записываются в буквенной форме. По аналогичной схеме изучается вычитание и умножение десятичных дробей.

В настоящее время наибольшее распространение получил первый подход и изучении десятичных дробей. Обязательный уровень теоретических знаний и умений учащихся по данному разделу ограничивается знанием формулировок правил, однако должна проводиться и работа, направленная на понимание смысла некоторых действий с десятичными дробями. Например, при изучении умножения и деления десятичной дроби на натуральное число полезно обсуж­дение с учащимися таких вопросов:

1. смысл умножения десятичной дроби на натуральное число;

2. появление нулей между запятой и значащей цифрой в произведении десятичной дроби на натуральное число;

3. смысл деления десятичной дроби на натуральное число;

4. проверка умножением деления десятичной дроби на натуральное число.

1 [онятие обыкновенной дроби вводится в 5 классе через понятие доли. Здесь же изучается сравнение дробей, рассматриваются правильные и неправильные дро­би, сложение и вычитание дробей с одинаковыми знаменателями, устанавливается снизь между делением и дробями, вводятся смешанные числа и правила сложения и вычитания этих чисел.

Необходимо подчеркнуть, что сложение дробей с одинаковыми знаменате-

2. ими состоит в подсчете одинаковых долей, содержащихся в данных дробях вме­сто, то сеть определение сложения дробей мало отличается от определения сложе­ния целых чисел. Определение сложения обыкновенных дробей с равными знаме-

нагелями заменяется правилом сложения дробей, знакомство с которым осуществ­ляется через решение задач. Вычитание дробей с равными знаменателями рассмат­ривается одновременно со сложением дробей. Здесь необходимо разъяснить смысл

операции вычитания дробей. Например, вычесть из дроби ~ дробь Д - это значит

5 7

найти такую дробь, которая при сложении с дробью - дает дробь -. Действие вы­читания в множестве рациональных чисел имеет такой же смысл, как и действие вычитания в множестве целых чисел.

В 6 классе основное внимание, в соответствии с подходом Н.Я. Виленкина, уделяется изучению действий с обыкновенными дробями: сложению, вычита­нию, умножению и делению. Сложение и вычитание обыкновенных дробей с раз­ными знаменателями сводится к сложению дробей с одинаковыми знаменателями через приведение дробей к общему знаменателю. Операция вычитания дробей рас­сматривается одновременно со сложением дробей.

При приведении дробей к общему знаменателю важно, чтобы учащиеся осознали замену их. равными дробями с одинаковым знаменателем. Поэтому не следует спешить с переходом к записи общего знаменателя под одной чертой.

_Т1 9 5 27 25 27 + 25 52

1 тпример, — + — = — + — = = —.

^{1 1} 20 12 60 60 60 60

9 5 27 + 25 52

1. Icmce можно записать короче: — + — = = —.

^г 20 12 60 60

11олозио обратить внимание учащихся на то, что, говоря о действии с дробями, иод термином дробь понимается дробное число (дробь - число) и, го­воря о сокращении дробей, иод термином дробь понимается запись дробного числа, символ (дробь-запись).

И учебнике Н.Я. Виленкина рассматривается сначала умножение дроби на натуральное число, а затем умножение дроби на дробь. Введение понятия умноже­ния дроби на число и дроби на дробь осуществляется через решение задач. Остано­вимся на этом подробнее. Учащимся предлагается решить две задачи:

3

Задача 1. В бутылке — л сока. Сколько сока в 5 таких бутылках?

3

Решение. Для решения задачи надо найти произведение - • 5. Но умно-

3. _с

жить - на натуральное число 5 - значит наити сумму пяти слагаемых, каждое из

3

которых равно —:

2-5=2+2 + 1 + 1 + 2 _ з + з + з + з + зз-5 is ,з

3. 44444 4 44 %'

3

Значит, в 5 бутылках 3 - л сока.

После этого формулируется правило.

«Чтобы умножить дробь на натуральное число, надо её числитель умно­жить на это число, а знаменатель оставить без изменения».

16

Затем решается вторая задача.

4. 2

Задача 2. Длина прямоугольника — дм, а ширина — дм (рис. 1). Чему равна

площадь прямоугольника?

Решение.Из рисунка видно, что данный прямоугольник можно получить так: разделить одну сторону квадрата со стороной 1 дм на 5 одинаковых частей и нчять 4 такие части, а другую сторону разделить на 3 одинаковые части и взять 2 такие части. При таком делении квадрат будет состоять из 15 равных частей, а пря­моугольник будет состоять из 8 таких частей. Значит, площадь прямоугольника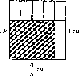

1 дм

равна — дм . Но мы знаем, что площадь прямо- угольника равна произведению длины и ширины. Поэтому считают, что число jj получено от ум-

4. 2 ножения - на -.

5. 3

Итак, - 5

2. _ 4-2 _ 8

3. 5-3 15'

Сразу после решения задачи формулиру-

ется правило. «Чтобы умножить дробь на

Рис. 1 дробь, надо: 1) найти произведение числителей

и произведение знаменателей этих дробей;

,’) первое произведение записать числителем, а второе - знаменателем».

Обычно вначале обозначают произведение числителей и произведение зна­менателей, а затем производят сокращение и только потом выполняют умноже­ние. В ответе, если это возможно, из дроби исключают целую часть. Например:

2. _ 14 _ 4 • 14 _ 4-2 _8 _ ■ 3 7 5 7-5 5 5 5

Введение правила умножения смешанных чисел осуществляется путем решения задачи на движение.

Задача 3. Сколько км проедет велосипедист за 1^ ч, если будет дви-

3

.'ыться со скоростью 9- км/ч?

I* е ш е н и е. Так как пройденный путь равен произведению скорости и

3 5

примени, то для решения задачи надо найти произведение чисел 9- и 1 —. Представим каждое из этих чисел в виде неправильной дроби:

о! = «.

2. 5 ’

12 12

Теперь воспользуемся правилом умножения дробей. Получим:

17 _ 48-17

12

₉3 . i_5_ ₌ 48 5 12 5

5-12

4-17 ₌ 68 _ ₁₃3 5 5 5'

4. 3

Таким образом, за 1 — ч велосипедист проедет 13 - км.

17

После решения задачи формулируется правило. «Для того чтобы выпол­нить умножение смешанных чисел, надо их записать в виде неправильных дро­бей, а затем воспользоваться правилом умножения дробей».

Ученикам сообщается, что с помощью умножения дробей решают такие же задачи, как и с помощью умножения натуральных чисел. Затем они знако­мятся с переместительным, сочетательным и распределительным свойствами умножения. Через решение задач осуществляется и введение понятий «нахож­дение дроби числа» и «числа по его дроби». Деление дробей рассматривается как действие, обратное умножению.

Необходимо заметить, что существуют и другае подходы к введению опера­ции умножения дроби на дробь, некоторые из них подробно освещенны в книге «Методика преподавания математики» под редакцией С. Е. Ляпина (Jlr, 1956).

Историческая справка

1. Десятичные дроби. Десятичные дроби впервые были использованы замечатель­ным узбекским ученым ал-К а ш и. В начале XV в. в Узбекистане, вблизи города Самаркан­да, была создана большая обсерватория. В ней производились наблюдения за движением звезд, планет и Солнца, вычислялись дни праздников и т.д. В обсерватории работали лучшие ученые того времени. Руководитель обсерватории ученый Джемшид ибн-Масуд ал-Каши был высокообразованным математиком и астрономом. Он оставил после себя много замеча­тельных математических открытий.

В 1427 г. ал-Каши закончил книгу «Ключ к арифметике». В этой книге он впервые в мире употребляет десятичные дроби, дает правила действия с ними, поясняет эти правила на примерах, подробно описывает новую, открытую им систему записи дробей. Для обозначе­ния разрядов он писал по-разному: отделял вертикальной черточкой, писал разными черни­лами, иногда выписывал название разряда полностью словами.

До этого в практике люди пользовались только обыкновенными и шестидесятичными дробями. О возможности десятичных дробей не догадывались даже величайшие ученые древней Греции. Д. Г. ал-Каши умер около 1456 года. Год рождения его неизвестен.

Труды ал-Каши долго не были известны европейским ученым. Они упорно искшш и, наконец, нашли новый вид дробей, более простой и более удобный - десятичные дроби. В Европе впервые подробно описал десятичные дроби талантливый фламандский инженер и ученый Симон Стевин (1548 - 1620). В книге «О десятой», изданной в 1585 году, Сте- вин подробно описал правила действий и преимущества открытых им десятичных дробей.

Стевин не был знаком с трудами ал-Каши и действительно открыл десятичные дроби. Но он открыл открытое. Первенство принадлежит Джемшиду ал-Каши, опередившему Сте- вина на полтора века. В Европе предшественником Стевина в середине XIV в. Был Бонфильс во Франции.

Ставить запятую после целой части десятичной дроби предложил знаменитый немец­кий ученый Кеплер (1571 - 1630). До Кеплера после целой части ставили нуль в скобках, на­пример, 3,7 писали как 3(0)7, отделяли вертикальной чертой (3|7) или писали разными чер­нилами, например целую часть числа черными, а дробную красными.

18