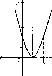- •Цели, содержание и структура курса математики 5-6 классов
- •Значение и место учения о числе в курсе математики общеобразовательной школы
- •5 Класс
- •6 Класс
- •3. Различные пути расширения понятия числа
- •4. Методика изучения натуральных чисел
- •4. Методика изучения натуральных чисел
- •5. Основные вопросы методики изучения дробей
- •5. Основные вопросы методики изучения дробей
- •6. Методика изучения положительных и отрицательных чисел
- •I. Основные типы преобразований и этапы их изучения
- •III этап. Организация целостной системы преобразований (синтез).
- •Буквенной части слагаемых пока остается первой.
- •1. Содержание и роль линии уравнений и неравенств в современном школьном курсе математики
- •2. Основные понятия линии уравнений и неравенств
- •I * hi лаже он и возникает по ходу обсуждения процесса решения, то ответ на не-
- •Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
- •* Последовательность изучения линии уравнений и неравенств
- •I )гапы изучения линии уравнений, неравенств и их систем в основной школе
- •1* Курсе математики 5 класса понятие уравнения трактуется аналогично.
- •Основные классы неравенств изучаются сразу вслед за изучением со- »»I мотствующих классов уравнений.
- •I Ъшить уравнение - это значит найти все его корни или установить, что их нет.
- •Решение квадратных уравнений и неравенств
- •Il Графический метод (I способ)
- •Графический метод
- •Системы уравнений с двумя переменными, в которых одно или оба уравнения второй степени
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Il Графический метод
- •Il Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •1. Цели обучения решению текстовых задач
- •2. Пропедевтика алгебраического и геометрического методов решения текстовых задач
- •3. Этапы решения задач на составление уравнений и их реализация
- •Этап {перевод задачи на геометрический язык).
- •Этап (решение задачи на геометрическом языке).
- •1. Из истории введения понятия функциональной зависимости в школьный курс математики
- •2. Различные трактовки понятия функции
- •3. Методика введения понятия функции
- •Этап. Мотивация введетя понятия.
- •Исследовать функцию на основные свойства.
- •Использовать изученные свойства функций при решении различных задач, в частности уравнений и неравенств.
- •Влияние коэффициентов hub на поведение функции
- •Взаимное расположение графиков линейных функции
- •Б. Интеграция аналитического и графического методов в изучении квадратичной функции
- •1. Цели и задачи курса геометрии основной школы
- •2. Содержание обучения геометрии в 7-9 классах
- •3. Логические основы изложения геометрии в 7-9 классах
- •Аксиомы принадлежности
- •Аксиомы порядка
- •Аксиомы измерения отрезков и углов
- •Рекомендуемая литература
- •1. Методика изучения основных свойств простейших геометрических фигур
- •1. Учебник а. В. Погорелова: § 1 «Основные свойства простейших геометрических фигур»,
- •Определения «через ближайший род и видовые отличия»
- •Измерение отрезков и углов
- •3. Учебник а. Д. Александрова и др,: глава I «Начала геометрииж
- •2. Методика формирования геометрических понятий
- •3, Обучение решению задач на первых уроках геометрии
- •II группа
- •1. Различные подходы к формированию понятия равенства фигур
- •Что нужно знать, чтобы утверждать равенство треугольников abc и dek1
- •На рисунке 55 изображено два равных треуголь- ника. Написать равенство этих треугольников, обозначив их вершины.
- •Если разносторонние треугольники abc и dkm
- •11Ри иодом пример.
- •I (сн тральное место в изучении равных треугольников занимают признаём риионота треугольников.
- •Доказательство:
- •Доказательство:
- •Треугольники вас и cdb равны. Напишите все соотношения, из ко- торых следует равенство указанных треугольников.
- •Напишите соотношение между элемен- тами треугольников abc и adc, из которых следовало бы их равенство.
- •Какие методические подходы существуют к введению понятия ранено гва фигур в школьном курсе геометрии? Какой подход, на Ваш взгляд, милмется наиболее удачным?
- •В чем особенности введения понятия равных треугольников в разных учебниках геометрии?
- •Приведите примеры упражнений на усвоение понятия равных треугольников.
- •I. Цели и этапы изучения взаимного расположения прямых на плоскости
- •1 Различные подходы к введению понятия параллельности прямых на плоскости.
- •I. Методика изучения признаков параллельности прямых.
- •1, Цели и этапы изучения взаимного расположения прямых на плоскости
- •2. Различные подходы к введению понятия параллельности прямых на плоскости
- •4. Методические замечания к изучению перпендикулярности прямых на плоскости
- •В данной плоскости через точку вне данной прямой можно провести только одну прямую, параллельную данной.
- •Сумма внутренних углов треугольника равна 2d.
- •1. Различные подходы к изучению многоугольников
- •2. Методика изучения четырехугольников
- •Если в четырехугольнике противоположные стороны попарно равны,
- •Если в четырехугольнике диагонали пересекаются и точкой пересечении делятся пополам, то этот четырехугольник параллелограмм.
- •Какие из систем неравенств задают на плоскости трапецию и почему? Покажите штриховкой множество точек плоскости, заданное системой неравенств:
- •1 H найти площадь трапеции.
- •1, Имеет1 ли ось симметрии фигура, заданная системой неравенств:
- •Верно ли утверждение: а) любой правильный многоугольник является выпуклым; б) любой выпуклый многоугольник является правильным?
- •Чему равны градусные меры углов: а) правильного пятиугольника; б) правильного двенадцатиугольника; в) правильного тридцатишестиугольника?
- •Множество направленных отрезков плоскости.
- •Множество классов направленных отрезков плоскости.
- •Множество параллельных переносов плоскости.
- •Начертите равнобочную трапецию: а) существуют ли векторы, определяемые её вершинами и равные по длине? б) Сколько пар сонаправленных векторов задают вершины трапеции?
- •Сколько пар сонаправленных (противоположно направленных) векторов определяют вершины параллелограмма?
- •Начертить параллелограмм, обозна- чить его вершины и написать все равные ме- жду собой векторы, началом и концом кото- рых являются вершины параллелограмма.
- •Векторы а и ъ равны, что следует из этого?
- •3. Методика изучения действий с векторами
- •II. Умножение вектора на число
- •Учебник геометрии а. В. Погорелова.
- •Учебник геометрии j1. С. Атанасяна и Др.
- •Построить вектор, представляющий сумму
- •4. Методика обучения решению задач с помощью векторов
- •1. Дан многоугольник abcde. Представьте ad в виде суммы: а) двух; б) I рёх; в) четырех векторов, заданных вершинами этого многоугольника.
- •Представьте вектор ав в виде суммы векторов ас, dc , bd .
- •Вектор cDколлинеарен вектору ав и Выразите один век-
- •Четырехугольник abcd - квадрат. Упростите выражение { ав - 3 вс)2,
- •VI. Упражнения на нахождение длины вектора и величины угла между векторами.
- •Какие действия с векторами изучаются в школьном курсе геометрии?
- •Б) в треугольнике лвс известны длины всех сторон. Определить его углы.
- •II кн. До н. Э.) уже фактически пользовался прямоугольными координатами.
- •Простейшие задачи в координатах на плоскости
- •Уравнения фигур на плоскости
- •4. Особенности применения метода координат
- •5. Методика формирования координатного метода решения задач
- •Решение (координатный метод)
- •Iэтап(оптимальный выбор прямоугольной системы координат). Выберем прямоугольную систему координат так, как показано на рис. 93.
- •Этап (перевод задачи на координатный
- •Так как м середина стороны вс, то л/
- •Этап (решение задачи на координат- ном языке).
- •Рекомендуемая литература
- •Значение тригонометрических функций в школьном курсе математики и различные подходы к их изложению
- •I ермипы «косинус», «котангенс» и др. Появились в XI—XVII вв.
- •Этапы изучения линии уравнений, неравенств и их систем в
- •Системы уравнений с двумя переменными, в которых
- •Цели и этапы изучения взаимного расположения прямых на
- •Различные подходы к введению понятии параллельности пря
Задача.
Квадрат
периметра прямоугольника, основание
которого больше высоты на 1 см, больше
площади этого прямоугольника на 34 см..
Найти высоту прямоугольника.
В
ходе решения учащиеся приходят к выводу,
что площадь прямоугольника равна х
(х + 1) см2,
а периметр равен (4х + 2) см, тогда квадрат
периметра равен (4х + 2)2
см2.
Так как по условию задачи квадрат
периметра прямоугольника больше площади
прямоугольника на 34 см2,
то можно составить уравнение:
х
(х + 1) + 34 = (4х + 2)2
После
преобразований получаем следующее
квадратное уравнение:
х
+ х
— 2
= 0.
Корнями
полученного уравнения являются х\
-
1 и х2
= -2. Так как дли- на отрезка не может быть
отрицательным числом, то искомая высота
равна 1
см. Вместе с этим каждое из выражений
уравнения х (х + 1) + 34 = (4х + 2)2
или х2
+ х н~ 34 = 16х2
+ 16х + 4 можно рассматривать как функцию
у~х2
+ х + 34яу
=
16х2
+ 16х - 30. Для каждой из них можно построить
график. Если графики построить в одной
системе координат, то они пересекутся.
Абсциссы точек пересечения х\
= 1 и х2
= -2
дают то значение аргумента, при котором
рассматриваемые функции равны (у(1) = 36
и у(-2)
= 36). Но так как нам надо найти высоту
прямоугольника, а длина отрезка
отрицательной быть не может, то искомая
высота принимает значение х = 1.
Можно
рассмотреть другие задачи, подобные
данной, решение которых приводит к
квадратным уравнениям. Таким образом,
учащиеся приходят к выводу, что квадратные
уравнения, как и уравнения первой
степени с одной переменной, тоже могут
решаться геометрическим (графическим)
методом.
Приведем
примеры параллельного решения квадратных
уравнений и неравенств алгебраическим
и графическим методами.
ПримерЗ,
Решить квадратное уравнение х2
- 4х + 3 = 0 и соответствующие ему
неравенства: х2
- 4х + 3 > 0 и х2
- 4х + 3 < 0.
Решение./.
Алгебраический
метод
х2
- 4х + 3 = 0,
по общей формуле корней квадратного
уравнения имеем:
4
±
Jl6
-12
4 ± 2
х\2~ — = ;
2
2
откудаxi
= 3,х2
= 1. О т в е т: Xi
= 3, х2
= 1.
Построим
график функции у
= х2-
4х + 3. Построение будем проводить по
следующей схеме:
Найдем
координаты вершины параболы и уравнение
оси параболы.
Имеем
а
=
1,
Ь
-
-4, тогда х0
= = 2;
у0
= {(2)
= 22-
4*2 + 3 = -
а
2
1.Значит,
вершиной параболы является точка (2;
-1),
а осью параболы - прямая х = 2.
Возьмем
какую-нибудь точку, принадлежащую
параболе, например,
74Il Графический метод (I способ)
(0;
3) и построим ей симметричную относительно
оси параболы, получим
точку (4; 3).
Через
полученные три точки (2; -1),
(0; 3), (4; 3)
проводим параболу (рис. 6).
Корнями
уравнения х2
- 4х + 3 = 0 служат
абсциссы точек
пересечения параболы с
осью ОХ.
Таких
точек две: (1; 0) и (3; 0).
Итак,
х\
= 1,Х2=
3.
Решив
графическим методом уравнение,
решаем
сразу же соответствующие ему не-
равенства:
х2
-
4х + 3 > 0 и х
-
4х + 3 < 0,
используя построенный
график. Решить
данные неравенства
графически - это зна-
чит ответить
на вопрос, при каких значе-
ниях
х ординаты точек параболы положительны
(для первого неравенства) и
отрицательны
(для второго неравенства). Из рисунка
6
видим, что график
функции расположен
выше оси ОХ
при х
< 1 и при х
> 3.
Значит,
решениями неравенства х2
- 4х
+ 3 > 0 служат все точки, принадлежащие
промежуткам х < 1
и х
>
3.
Аналогично,
для неравенства х2
- 4х + 3 < 0 замечаем, что график функции
расположен ниже оси ОХ
при 1 < х < 3. Этот промежуток и является
решением неравенства.
Для
проверки полученных ответов решаем
неравенства х2
- 4х + 3 > 0 и х2
- 4х + 3 < 0 аналитически, с помощью системы
неравенств или методом интервалов
(после его изучения).
После
решения двух (трех) аналогичных уравнений
и соответствующих им неравенств учащиеся
могут сделать выводы по геометрической
интерпретации их решений, а именно:
1. Если
квадратное уравнение ах
+ Ьх
+ с
= 0
имеет два корня,
то
геометрически это означает, что парабола
- график
функции у
= ах2
+ Ьх
+ с- пересекает ось ОХ в двух точках,
абсциссы которых и являются корнями
данного уравнения. Верно и обратное:
если
парабола - график функции у
= ах2
+ Ьх
+ с- пересекает ось ОХ в двух точках,
то
квадратное уравнение ах2
+ Ьх
+
с = 0
имеет два корняу которыми являются
абсциссы точек пересечения.
2. Если
квадратное неравенство ах + Ьх + с> 0
(ах2
+ Ьх + с < 0) имеет решения (но выполняется
не при всех значениях х), то геометрически
это означает,
что
часть параболы - графика функции у =
ах
+ Ьх+ с-расположена выше
(ниже)
оси ОХ. Верно и обратное: если часть
параболы - графика функции у
= ах
+ Ьх
+ с
- расположена
выше
(ниже)
оси ОХ, то это означает, что квадратное
неравенство ах2
+ Ьх + с> 0 (ах2
+ Ьх + с<0)
имеет решения.
Следует
заметить, что графический метод решения
квадратных уравнений'и неравенств
включает, кроме рассмотренного, ещё
четыре способа решения. Приведем их
схемы.
75
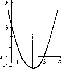
способ.
Преобразуем уравнение к виду х
~ 4х -
3, затем построим в
одной системе
координат графики функций >> = х2
и у - 4х -
3. Корнями урав-
нения служат абсциссы
точек пересечения параболы и прямой
- графиков
этих функций.
способ.
Преобразуем уравнение к виду х2
+ 3 = 4х, затем построим в
одной системе
координат графики функций^ = х2
+ 3 и
у
= 4х.
Корнями урав-
нения являются абсциссы
точек пересечения параболы и прямой
- графиков
этих функций.
способ.
Преобразуем уравнение к виду х2-4х
+ 4-1=0и
далее
х2
- 4х
+ 4 = 1, т.е. (х - 2)2
= 1. Построим в одной системе координат
параболу
у
= (х-
2)2
и прямую у
=
1. Корнями уравнения служат абсциссы
точек пере-
сечения графиков этих
функций.
способ.
Разделив почленно обе части уравнения
на х, получим
4 4
х-4
+ - = 0
и далее х
- 4 =
— . Построим в одной системе координат
ги-
я *
4
перболу
у
=
— и прямую у
= х-
4. Корнями уравнения являются абсциссы
х
точек
пересечения графиков данных функций.
Пример
4. Решить квадратное уравнение 4х2
- 4х + 1 = 0 и соответ-
ствующие ему
неравенства: 4х2
- 4х + 1
> 0
и 4х2
- 4х + 1 < 0.
Решение./.
Алгебраический
метод
4х2
- 4х + 1 = 0, по формуле корней квадратного
уравнения имеем:
_
4 + д/42
- 4*4 4 ± 0 1
Х\2~
= — —. .
2-4 8
2 •'
^
1
Ответ:
х=
—.
2
//.
Графический
метод (I способ)
Построим
график функции^ = 4х2
- 4х + 1. Найдем сначала координаты
вершины
параболы. а = 4, й = - 4, х0
= ~ Уо=
f(^)=
0.
Значит,
вершиной параболы является точка (^;
0), а осью параболы
прямая
х = ^. Также как и в примере 3, выполняем
построение графика (рис, 7).
Как
видим из рисунка, парабола имеет с
осью
ОХ
только одну общую точку (~; 0). Значит,
данное
квадратное уравнение имеет только один
1
корень:
х = -.
Построенный
график позволяет сразу же
решить
и квадратные неравенства: 4х2
- 4х + 1 >0
и 4х2
- 4х + 1 < 0.
Из
рисунка видно, что вся парабола, кроме
Рис.
7 одной её точки, которая лежит на оси
ОХ,
распо-