2. Найдем абсциссы точек пересечения трафиков, решив уравнения:

-4х + 3 = 3 и 4х - 3 = 3.

л - ³ х\ = 0, х₂ - -.

3. Геометрически решить данное неравенство - это значит, найти те значе- ния х, при которых график функции у\ расположен не ниже прямой у₂ = 3. Из ри-

3

сунка видим, что это условие выполняется при х < О и х > —.

3

Отв ет:х< О,х> - .

2

В данном случае алгебраический метод оказался более рациональным, чем графический. Преимущество графического метода в его наглядности. Часто в неравенствах встречается не один, а несколько модулей, приведем примеры.

Пример 23. Решить неравенство | 5 - х I > 21 х — 21.

Решение./. Алгебраический метод

1. Разобьем всю числовую прямую на три промежутка: (- оо; 2), [2; 5] и (5; +оо). На каждом из этих промежутков запишем данное неравенство без модуля и решим его.

А) На промежутке (-од; 2) верны равенства [ 5 -х| = 5 -х и | х-2 [ = -х +

2. и наше неравенство примет вид:

5-х > ~2х + 4, откудах > -1.

Учитывая данный промежуток, получаем решение исходного неравен- ства на этом промежутке: -1 < х < 2.

Б) На промежутке [2; 5] верны равенства |5-х| = 5- хи | х - 21 = х - 2, поэтому наше неравенство примет вид:

5-х > 2х - 4, откуда х < 3.

Учитывая данный промежуток, получаем решение неравенства на этом

промежутке: 2 <х < 3.

В) На промежутке (5; +оо) верны равенства |5-х| = -5+хи || х - 2 I = х - 2, поэтому неравен- ство примет вид:

-5 + х > 2х - 4, откуда х < -1. Учитывая данный проме- жуток, получаем, что решений на этом промежутке неравенст- во не имеет.

Отв ет: -1 <х < 3.

2. Графический метод

1. Построим в одной сис- теме координат графики функ- ций = | 5 - х | и>^,2 = 2|х-2| (рис. 28).

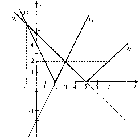
2. Абсциссы точек пересечения графиков найдем, решив уравнения:

2. -х = -2х + 4 и 5 -х = 2х - 4, откудах\ ~ -1,х₂= 3.

3. Геометрически решить данное неравенство- это значит, найти те значения х, при которых график функции у_} расположен не ниже графика функции у2⁼ 21 х — 21.

Из рисунка видим, что это условие выполняется при -1 < х < 3.

О т в е т: -1 <х < 3.

Графический метод, как мы видим, здесь является более рациональным, наглядным и не требует каких-либо особых умений, кроме умений выпол- нять построение графика функции, содержащей модуль.

Пример 24. Решить неравенство I х - ll +1 х + ll < 4.

Решение./. Алгебраический метод

1. Разобьем всю числовую прямую на три промежутка: (- оо; -1), [-1; 1] и (1; +оо). На каждом из этих промежутков запишем данное неравенство без модуля и решим его.

1. На промежутке (- сю; -1) верны равенства

|x-l|=-x+l и|х+ll =-х-1, и наше неравенство примет вид: -2х < 4, откуда х > -2.

Учитывая данный промежуток, получаем решение исходного неравен- ства на этом промежутке: -2 < х < -1.

Б) На промежутке [-1; 1] верны равенства

|x-l|=-x+l и|х+1|=х+1, поэтому наше неравенство равносильно верному числовому неравенству 2 < 4, значит, все значения переменной, принадлежащие этому отрезку, входят в множество решений.

2. На промежутке (1; +оо) верны равенства

|х-1|=х-1и |х + 1 I = Х+ 1, поэтому получаем, что наше неравенство равносильно линейному неравенст- ву 2х < 4, откуда х < 2.

Учитывая данный промежуток, по-

лучаем решение исходного неравенства на этом промежутке: 1< х < 2. Объединяя по- лученные результаты, делаем вывод: нера- венству удовлетворяют все значения пере- менной из интервала -2 < х < 2 и только они.

О т в е т: -2 < х < 2.

2. Графический метод

1. Построим в одной системе коорди- нат графики функций у_г = | х - l| + | х + l| и У2 = 4. Построение графика функции у\ выполняем отдельно на каждом из про- межутков (- оо; -1), [-1; 1] и (1; +оо). На промежутке (- оо; -1) это будет график функ-

100

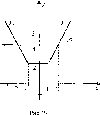
цшу = ~2х, соответственно, на двух других промежутках у = 2яу = 2х (рис. 29). На интервале -2 <х <2 график функции у\ расположен под графиком функ- ции уг_ь т.е. неравенство у₂ < 4 справедливо.

О т в е т: -2 <х < 2.

Можно было бы решить данное неравенство графически, преобразовав его сначала к виду:

I х - ll < -1 х + ll + 4.

Рассмотрим случай, когда неравенство, содержащее модуль, выполня- ется при любом значении х.

Пример 25. Решить неравенство I 2х -1| > I х + l| - 2.

Решение./. Алгебраический метод

L Разобьем всю числовую прямую на три промежутка: (~ со; -1), [-1; ~]

и (А; +°°). На каждом из этих промежутков запишем данное неравенство без

модуля и решим его.

1. На промежутке (- сю; -1) верны равенства

1. 2х -11 = - 2х + 1 и I х + l| = =- х -1, и наше неравенство примет вид: -2х + 1>-х-1~2, откуда х < 4.

Учитывая данный промежуток, получаем решение исходного неравен- ства на этом промежутке: х < -1.

Б) На промежутке [-1; ] верны равенства

1. 2х ~11 =-2х+ 1 и|х+1|=х+1, поэтому наше неравенство равносильно неравенству: -2х + 1 > х + 1 - 2, от-

2. 1 куда х < -,тогда решением неравенства будет данный промежуток -1 < х < -.

2. На промежутке (^; +а>) верны равенства

I 2х- ll = 2х -1 и |х + 11 = х+ 1,

поэтому получаем, что наше не- равенство равносильно неравен- ству: 2х - 1 > х - 1, откуда х > 0.

Учитывая данный проме- жуток, получаем решение ис- ходного неравенства на этом

промежутке: ^{х >}~- Объединяя

полученные результаты, делаем вывод: неравенству удовлетво- ряет любое число х.

О т в е т: х - любое.

//. Графический метод

1. Построим в одной сис- теме координат графики функ-

101

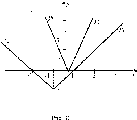
ций^ = I 2x - ll иу₂ = \x + l| - 2 (рис. 30).

2. Геометрически решить данное неравенство- это значит, найти те значения х, при которых график функции у\ расположен не ниже графика функции72? то есть над графиком или на графике функции^*

Из рисунка видно, что график функции у\ всегда расположен выше гра­фика функции^, поэтому неравенство выполняется при любом значении х.

Таким образом, рассмотренные примеры позволяют сделать следующие выводы:

1. Интеграция алгебраического и графического методов решения урав­нений и неравенств с одной переменной, систем уравнений с двумя перемен­ными имеет большое значение в плане повышения качества знаний учащихся и одновременного развития всех трёх компонентов их математических спо­собностей (алгебраического, логического и геометрического).

2. Графический метод позволяет обучать учащихся геометрическому моделированию при решении уравнений, , неравенств и их систем. При этом выполняются все три этапа математического моделирования: 1) построение геометрической модели задачи (т.е. перевод уравнения, неравенства, системы уравнений или неравенств на геометрический язык); 2) решение уравнения, неравенства, системы уравнений (неравенств) на геометрическом языке; 3) интерпретация (т.е. перевод полученного решения с геометрического языка на алгебраический).

3. Графический метод в ряде случаев является единственным средством приближенного решения уравнений и систем уравнений, в других - он дает возможность наиболее просто определить количество действительных реше­ний, найти промежутки, в которых лежат искомые корни, определить их приближенные численные значения. Задания такого типа часто встречаются в части «С» заданий Единого государственного экзамена.

4. Применение наряду с алгебраическим графического метода в школе имеет и воспитательное значение - построение графиков приучает учащихся к самостоятельности в работе (списать решение уже трудно), к точности, ак­куратности.

5. Графический метод способствует эстетическому воспитанию школь­ников, прививает вкус к изящным, красивым решениям алгебраических задач.

Вопросы и задания

1. Как трактуется понятие уравнения в 5-6-х классах?

2. Как решаются уравнения в 5 классе (в 6 классе)?

3. Какие уравнения изучаются в 7 классе и на чем основан метод их решения?

4. Какие существуют подходы к изучению линейных уравнений с одной переменной (с одним неизвестным)?

5. Какие типы уравнений изучаются в 8-9 классах? Опишите способы их решения. Приведите соответствующие примеры.

102

6. Как вводится понятие системы двух линейных уравнений с двумя неизвестными? Каковы особенности изучения этой темы в школьном курсе математики?

7. Опишите методику введения понятия квадратного уравнения и алго­ритм его решения.

8. Как представлен вывод формулы корней квадратного уравнения в учебниках алгебры разных авторов?

9. Назовите особенности изучения неравенств в школьном курсе математики.

10. Опишите методику введения понятия линейного неравенства с од­ним неизвестным.

11. .Что понимается под интеграцией алгебраического и геометрическо­го методов решения задач?

12. Каков алгоритм построения параболы при решении квадратного уравнения (или неравенства) графическим методом? Приведите примеры.

13. Какие существуют способы решения квадратного уравнения (или неравенства) графическим методом? Приведите примеры.

14. Какое уравнение называется иррациональным? Как можно мотиви­ровать введение понятия иррационального уравнения?

15. Назовите алгебраические методы решения иррациональных уравне­ний. Какой из них наиболее часто используется в школьной практике?

16. Составьте (подберите из учебников) 2-3 уравнения или неравенства с модулем и решите каждое из них алгебраическим и графическим методами.

17. Какие умения необходимы учащимся для овладения ими графиче­ским методом решения уравнений (неравенств), содержащих модуль?

Рекомендуемая литература

1. Автономова, Т. В. Практикум по методике преподавания математики в средней шко- ле:Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / Т.В. Автономова, С.Б. Вер­ченко, В А. Гусев и др.; Под ред. В.И. Мишина. - М.: Просвещение, 1993.

2. Д а л и н г е р, В. А. Геометрия помогает алгебре / В.А. Далингер // Математика в шко­ле. - 1996. -№ 4. - С. 29 - 34.

3. Далингер, В. А. Методика реализации внутрипредметных связей при обучении ма­тематике: Кн. для учителя. - М.: Просвещение, 1991

4. 3 в а в и ч, Л. И. Тригонометрические уравнения / ЛИ. Звавич, Б.П. Пигарев // Матема­тика в школе. - 1995. - № 2 и № 3. - С. 18-27.

5. Капкаева, Л. С. Интеграция алгебраического и геометрического методов при обучении математике в школе: Учеб. пособие для студ. мат. спец. пед. вузов /Л.С. Капкаева. - Саранск, 2003.-179 с..

6. Лабораторные и практические работы по методике преподавания математики: Учеб. по­собие для студентов физ.-мат. спец. пед. ин-тов / Е.И. Лященко, К.В. Зобкова. Т.Ф. Кири­ченко и др.; Под ред. Е.И. Лященко. - М.: Просвещение, 1988.

7. Методика и технология обучения математике. Курс лекций: пособие для вузов / под научн. ред. Н. Л. Стефановой, Н. С. Подходовой. - М.: Дрофа, 2005. - 416 с.

8. Методика преподавания математики в средней школе: Частная методика: Учеб. по­собие для студентов пед. ин-тов по физ.-мат. спец. /А.Я. Блох, В.А. Гусев, Г.В. Дорофе­ев и др.; Сост. В.И. Мишин. - М.: Просвещение, 1987.

103

9. М о д е н о в, В. П. Грани математики: координатно-параметрический метод / Ш! Моденов. - М.; Издат. отдел УНЦ ДО МГУ, 1999.

10. М о р д к о в и ч, А. Г. Математика в школе - новые задачи, новые концепции, Новы! учебники / А. Г. Мордкович // Модернизация школьного математического образования и проблемы подготовки учителя математики: Труды XXI Всероссийского семи пари препод. математики ун-тов и пед. вузов. - СПб.: Изд-во РГПУ им. А. И. Герцена, 2002. С. 3-12.

11. П е т е р с о н, Л. Г. Математика: 3 класс: в 4-х ч. Ч. 1. - М.: Изд-во «Баласс», 1996.

12. Г а л и ц к и й, М. Л. и др. Сборник задач по алгебре для 8-9 классов: Учеб. пособие для учащихся шк, и классов с углубл. изуч. математики / М. Л. Галицкий, А. М. Гольдман,

Л. И. Звавич. - 2-е изд. - М.: Просвещение, 1994. - 271 с.

9. Пособие по математике для поступающих в вузы: Учеб. пособие / Кутасов А. Д„ Пиголкина Т. С., Чехлов В. И., Яковлева Т. X. - Под ред. Г. Н. Яковлева. - 3-е изд, перераб. - М.: Наука, 1988. - 720 с.

10. Сборник задач по математике для поступающих во втузы / В. К. Егерев, В. В. Зайцев, Б. А. Кордемский и др.; Под ред. М. И. Сканави. - 6-е изд. - М., 2005. - 608 с.

11. Школьные учебники по алгебре и алгебре и началам анализа (см. лекцию № 2).

12. http://www.allmath.ru/

13. http://www.erudition.ru/referat/ref/id.34302 1 .html

14. http://www.uztest.ru/abstracts/?idabstract^r=30

15. http://www.bibliofond.ru/view,aspx?id^r:r5625

104