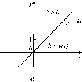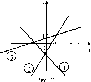- •Цели, содержание и структура курса математики 5-6 классов
- •Значение и место учения о числе в курсе математики общеобразовательной школы
- •5 Класс
- •6 Класс
- •3. Различные пути расширения понятия числа
- •4. Методика изучения натуральных чисел
- •4. Методика изучения натуральных чисел
- •5. Основные вопросы методики изучения дробей
- •5. Основные вопросы методики изучения дробей
- •6. Методика изучения положительных и отрицательных чисел
- •I. Основные типы преобразований и этапы их изучения
- •III этап. Организация целостной системы преобразований (синтез).
- •Буквенной части слагаемых пока остается первой.
- •1. Содержание и роль линии уравнений и неравенств в современном школьном курсе математики
- •2. Основные понятия линии уравнений и неравенств
- •I * hi лаже он и возникает по ходу обсуждения процесса решения, то ответ на не-
- •Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
- •* Последовательность изучения линии уравнений и неравенств
- •I )гапы изучения линии уравнений, неравенств и их систем в основной школе
- •1* Курсе математики 5 класса понятие уравнения трактуется аналогично.
- •Основные классы неравенств изучаются сразу вслед за изучением со- »»I мотствующих классов уравнений.
- •I Ъшить уравнение - это значит найти все его корни или установить, что их нет.
- •Решение квадратных уравнений и неравенств
- •Il Графический метод (I способ)
- •Графический метод
- •Системы уравнений с двумя переменными, в которых одно или оба уравнения второй степени
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Il Графический метод
- •Il Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •1. Цели обучения решению текстовых задач
- •2. Пропедевтика алгебраического и геометрического методов решения текстовых задач
- •3. Этапы решения задач на составление уравнений и их реализация
- •Этап {перевод задачи на геометрический язык).
- •Этап (решение задачи на геометрическом языке).
- •1. Из истории введения понятия функциональной зависимости в школьный курс математики
- •2. Различные трактовки понятия функции
- •3. Методика введения понятия функции
- •Этап. Мотивация введетя понятия.
- •Исследовать функцию на основные свойства.
- •Использовать изученные свойства функций при решении различных задач, в частности уравнений и неравенств.
- •Влияние коэффициентов hub на поведение функции
- •Взаимное расположение графиков линейных функции
- •Б. Интеграция аналитического и графического методов в изучении квадратичной функции
- •1. Цели и задачи курса геометрии основной школы
- •2. Содержание обучения геометрии в 7-9 классах
- •3. Логические основы изложения геометрии в 7-9 классах
- •Аксиомы принадлежности
- •Аксиомы порядка
- •Аксиомы измерения отрезков и углов
- •Рекомендуемая литература
- •1. Методика изучения основных свойств простейших геометрических фигур
- •1. Учебник а. В. Погорелова: § 1 «Основные свойства простейших геометрических фигур»,
- •Определения «через ближайший род и видовые отличия»
- •Измерение отрезков и углов
- •3. Учебник а. Д. Александрова и др,: глава I «Начала геометрииж
- •2. Методика формирования геометрических понятий
- •3, Обучение решению задач на первых уроках геометрии
- •II группа
- •1. Различные подходы к формированию понятия равенства фигур
- •Что нужно знать, чтобы утверждать равенство треугольников abc и dek1
- •На рисунке 55 изображено два равных треуголь- ника. Написать равенство этих треугольников, обозначив их вершины.
- •Если разносторонние треугольники abc и dkm
- •11Ри иодом пример.
- •I (сн тральное место в изучении равных треугольников занимают признаём риионота треугольников.
- •Доказательство:
- •Доказательство:
- •Треугольники вас и cdb равны. Напишите все соотношения, из ко- торых следует равенство указанных треугольников.
- •Напишите соотношение между элемен- тами треугольников abc и adc, из которых следовало бы их равенство.
- •Какие методические подходы существуют к введению понятия ранено гва фигур в школьном курсе геометрии? Какой подход, на Ваш взгляд, милмется наиболее удачным?
- •В чем особенности введения понятия равных треугольников в разных учебниках геометрии?
- •Приведите примеры упражнений на усвоение понятия равных треугольников.
- •I. Цели и этапы изучения взаимного расположения прямых на плоскости
- •1 Различные подходы к введению понятия параллельности прямых на плоскости.
- •I. Методика изучения признаков параллельности прямых.
- •1, Цели и этапы изучения взаимного расположения прямых на плоскости
- •2. Различные подходы к введению понятия параллельности прямых на плоскости
- •4. Методические замечания к изучению перпендикулярности прямых на плоскости
- •В данной плоскости через точку вне данной прямой можно провести только одну прямую, параллельную данной.
- •Сумма внутренних углов треугольника равна 2d.
- •1. Различные подходы к изучению многоугольников
- •2. Методика изучения четырехугольников
- •Если в четырехугольнике противоположные стороны попарно равны,
- •Если в четырехугольнике диагонали пересекаются и точкой пересечении делятся пополам, то этот четырехугольник параллелограмм.
- •Какие из систем неравенств задают на плоскости трапецию и почему? Покажите штриховкой множество точек плоскости, заданное системой неравенств:
- •1 H найти площадь трапеции.
- •1, Имеет1 ли ось симметрии фигура, заданная системой неравенств:
- •Верно ли утверждение: а) любой правильный многоугольник является выпуклым; б) любой выпуклый многоугольник является правильным?
- •Чему равны градусные меры углов: а) правильного пятиугольника; б) правильного двенадцатиугольника; в) правильного тридцатишестиугольника?
- •Множество направленных отрезков плоскости.
- •Множество классов направленных отрезков плоскости.
- •Множество параллельных переносов плоскости.
- •Начертите равнобочную трапецию: а) существуют ли векторы, определяемые её вершинами и равные по длине? б) Сколько пар сонаправленных векторов задают вершины трапеции?
- •Сколько пар сонаправленных (противоположно направленных) векторов определяют вершины параллелограмма?
- •Начертить параллелограмм, обозна- чить его вершины и написать все равные ме- жду собой векторы, началом и концом кото- рых являются вершины параллелограмма.
- •Векторы а и ъ равны, что следует из этого?
- •3. Методика изучения действий с векторами
- •II. Умножение вектора на число
- •Учебник геометрии а. В. Погорелова.
- •Учебник геометрии j1. С. Атанасяна и Др.
- •Построить вектор, представляющий сумму
- •4. Методика обучения решению задач с помощью векторов
- •1. Дан многоугольник abcde. Представьте ad в виде суммы: а) двух; б) I рёх; в) четырех векторов, заданных вершинами этого многоугольника.
- •Представьте вектор ав в виде суммы векторов ас, dc , bd .
- •Вектор cDколлинеарен вектору ав и Выразите один век-
- •Четырехугольник abcd - квадрат. Упростите выражение { ав - 3 вс)2,
- •VI. Упражнения на нахождение длины вектора и величины угла между векторами.
- •Какие действия с векторами изучаются в школьном курсе геометрии?
- •Б) в треугольнике лвс известны длины всех сторон. Определить его углы.
- •II кн. До н. Э.) уже фактически пользовался прямоугольными координатами.
- •Простейшие задачи в координатах на плоскости
- •Уравнения фигур на плоскости
- •4. Особенности применения метода координат
- •5. Методика формирования координатного метода решения задач
- •Решение (координатный метод)
- •Iэтап(оптимальный выбор прямоугольной системы координат). Выберем прямоугольную систему координат так, как показано на рис. 93.
- •Этап (перевод задачи на координатный
- •Так как м середина стороны вс, то л/
- •Этап (решение задачи на координат- ном языке).
- •Рекомендуемая литература
- •Значение тригонометрических функций в школьном курсе математики и различные подходы к их изложению
- •I ермипы «косинус», «котангенс» и др. Появились в XI—XVII вв.
- •Этапы изучения линии уравнений, неравенств и их систем в
- •Системы уравнений с двумя переменными, в которых
- •Цели и этапы изучения взаимного расположения прямых на
- •Различные подходы к введению понятии параллельности пря
После этого делается вывод, что графиком любой линейной функции является прямая. Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки в координатной плоскости и провести через них прямую.
В качестве упражнений можно рассмотреть примеры на построение графика линейной функции: 1) у = 2х + 3; 2) у = - 0,8х + 1.
Замечание 1.В7 классе принимают без доказательства тот факт, что графиком линейной функции является прямая линия. В 8 классе после изучения признаков подобия треугольников появляется возможность обосновать этот факт {попробуйте провести доказательство самостоятельно).
Замечание 2. Если область определения линейной функции состоит не из всех чисел, то её график представляет собой соответствующую часть прямой. Например, это может быть полупрямая или отрезок.
Влияние коэффициентов hub на поведение функции
1. При к = 0 формула у = кх + Ъ имеет вид у = Ох + Ъ, то есть у~Ь. Линейная функция, задаваемая формулой у = Ъ, принимает одно и то же значение при любом х, например, функция у = -2 принимает значение -2 при любом х. Функция у = b - это частный случай линейной функции. Её графиком является прямая, параллельная оси ОХ и проходящая через точку (0; -2).
Для учащихся построение графика функции у = Ъ представляет определенную трудность психологического характера, так как в такой формуле в явном виде не содержится переменная х. Поэтому можно рекомендовать записывать формулу у = b в виде у = Ох + Ъ, тогда, как и в общем случае, учащиеся
137
смогут
находить пары соответственных значений
х
и у.
(При этом в качестве х
берется
любое число, а значение у
при любом х
оказывается равным Ь.)
Желательно,
чтобы на первых же уроках учащиеся
усвоили, что графиком функции у
= b
служит
прямая, параллельная оси ОХ.\
и что при Ъ
= О мы получаем саму ось ОХ.
2.
Вторым частным случаем линейной функции
является прямая
пропорциональность.
Введение
прямой пропорциональности осуществляется
следующим образом. Рассматривается
пример: пусть V-
объем железного бруска в см3,
т -
его масса в г. Так как плотность железа
равна 7,8 г/см3,
то т
= 7,8 К
Зависимость
массы железного бруска от его объема
является примером функции, которая
задается формулой вида у
= кх9
где х
-
независимая переменная, к-
число, отличное от нуля. Такую функцию
называют прямой
пропорциональностью.
Затем формулируется определение.
Определение.
Прямой пропорциональностью называется
функция, которую можно задать формулой
вида у
= for,
где
х
- независимая переменная, к
- число,
отличное от нуля.
Учащимся
сообщается, что прямая пропорциональность
является частным случаем линейной
функции, так как формула у
= кх
получается из формулы;; = кх
+ Ъ
при Ъ~
0. Отсюда следует, что графиком прямой
пропорциональности служит прямая.
Эта прямая проходит через начало
координат, так как прих = 0
у
= 0.
Итак,
графиком
прямой пропорциональности является
прямая.,
проходящая
через начало координат.
Для
построения графика прямой пропорциональности
достаточно отметить какую-либо точку
графика, отличную от начала координат,
и провести через эту точку и начало
координат прямую. (Учащимся предлагается
построить график функции у
= 0,5х.)
Расположение
графика функции у
= кх
в координатной плоскости зависит от
коэффициента к.
Из формулы у
= кх
находим, что если х
= 1, то у
= к.
Значит, график функции у
= кх
проходит через точку (1; к).
При к
>
0 эта точка расположена в первой
координатной четверти, а при к
< 0 - в четвертой.
Отсюда
следует, что при к
>
0 график прямой пропорциональности
расположен в I и III координатных
четвертях, а при к
<
0 - во II и IV четвертях.
Итак,
обучив семиклассников построению
графика линейной функции, можно
приступить к элементарному исследованию
свойств этой функции. В 7-м классе
возможно аналитически выделить значения
аргумента, при которых линейная
функция принимает положительные
(отрицательные) значения, доказать
монотонность линейной функции. При
этом придется обходиться определениями
действий над положительными и
отрицательными числами. Все остальные
свойства (например, роль и геометрический
смысл коэффициентов в уравнении линейной
функции) можно установить из геометрических
соображений.
Достаточно
легко устанавливается, что коэффициент
Ъ
есть значение линейной функции при
х
= 0. Геометрически Ь
означает длину и положение на оси
ординат отрезка, отсекаемого графиком
функции, считая от 0 (вверх, если Ъ
> 0,
и
вниз, если Ъ
< 0) или иначе, это ордината точки
пересечения графика функции с осью OY
(абсцисса
этой точки всегда равна 0). А коэффициент
к
находится в случае прямой пропорциональности
у = кх
как к
= у(1),
В общем случае линейной функции как
к
= у(1)
- Ь,
Учащимся следует все это показать на
графиках функций (рис. 41а, б).
Рис.
41
Значительные
трудности представляет случай
отрицательных значений углового
коэффициента; для него требуется
отдельная работа, построенная аналогично.
Конечно,
необходимы упражнения в отыскании
коэффициентов линейной функции по
их графикам. Начальные упражнения
должны быть простыми и иметь своей
целью усвоение геометрического смысла
коэффициентов формулы, задающей
функцию. Приведем примеры.
Найдите
значения коэффициентов к
в уравнениях прямых у = hс,
изображенных на рисунке 42. Запишите
уравнения этих прямых.
а)
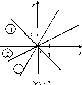
Найдите значения коэффициентов Ъ
для прямых у = кх
+ 6, изображенных на рисунке 43.
б) Каковы
числовые значения коэффициентов к
для этих прямых с точностью до 0,1?
в) Запишите
уравнения прямых, изображенных на этом
рисунке (измерения дадут приближенные
значения к
и Ь).
139