Простейшие задачи в координатах на плоскости

В первом случае с помощью теоремы Фалеса доказываем, что точка С\ является серединой отрезка А\В\ (АА_} || Оу, ВВ\ || Оу), С - середина АВ (рис. 83).

Из равенства A i С\ = В\С\ следует, что \ x-xi\ = \x-x₂\. Последнее равен­ство известно учащимся из курса алгебры. Поэтому либо х - Х\ - х - х₂, либо л: - х\ = - (х - хг). Первое невозможно, так как х\ *хъ Поэтому верно второе: х -

х\ = - х + Х2. Отсюда 2х = х\ + Х2, а х~ ** *-*²- - абсцисса точки С.

Если х{ ~ х₂, то есть АВ || Оу, то все три точки Ли В_} и С\ имеют одну и ту же абсциссу. Значит, формула остается верной и в этом случае.

Ордината точки С находится аналогично. Через точки А, В и С проводятся

прямые, параллельные оси Ох. В итоге получаем у = ^у-~ - ординату точки С.

б) Вычисление длины вектора по его координатам. В учебнике JI. С. Атана- сяна и др. доказывается, что длина вектора а (х; у) вычисляется по формуле

I а\= д/х² + / .

Для доказательства этой формулы отложим от начала координат вектор ОА = а и проведем через точку А перпендикуляры АА\ и АА₂ к осям Ох и Оу (рис. 84). Координаты точки А равны координатам векторов О А, т. е. (х; у). По­этому О А1 = | х\, АА\- ОА₂ = | у| (мы рассматриваем случай, когда х * 0 и у * 0; другие случаи учащиеся могут рассмотреть самостоятельно).

По теореме Пифагора

О А ^ ^ОА_} + ААj = -\fx² + у² .

Но | а\-\ОА\ = ОА, поэтому | а | = ^х²+у² , что и требовалось доказать.

238

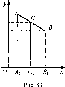
в) Нахождение расстояния между двумя точками по их координатам.

Формулы для вычисления расстояния между точками, координаты которых и тоеты, также рассматриваются для различных случаев расположения этих точек.

Найдем расстояние между точками А\ (хь у{) и А₂

fey₂).

а) Пусть х\ *х₂, иу1 Фу₂ (рис. 85).

В этом случае АА\ -1 у\ -у₂1; АА₂ = | x_Y-х₂|.

По теореме Пифагора

А_ХА₂ = (xi -х₂)² + (у\ -у₂)².

После этого рассматриваются другие возмож- ные случаи:

1. xi =х₂, yi *у₂;

2. xi *х₂, yi =у₂;

3. хх=х₂, иу!=у₂.

Полученная формула верна для каждого из

них случаев.

В учебнике JT. С. Атанасяна и др. иной подход к выводу формулы. Рас­сматривается вектор 4Л > находятся его координаты (если известны координа- H.I ого концов) и длина этого вектора через его координаты. В итоге получаем ntuyio же формулу.

2. Уравнения фигур на плоскости

В курсе алгебры, исходя из уравнения у =/(х), где/(х) - заданная функ­ции, строили кривую, определяемую этим уравнением, то есть строили график функции у =Хх). Таким образом, шли как бы «от алгебры к геометрии». При научении метода координат мы выбираем обратный путь: исходя из геометри­ческих свойств некоторых кривых, выводим их уравнение, то есть идем как бы * I геометрии к алгебре». В восьмом классе (по учебнику JI. С. Атанасяна в де­ти ом классе) рассматриваются уравнения окружности и прямой, а в десятом - \ |>;шисиия плоскости и сферы.

В учебнике А. В. Погорелова дается общее понятие «уравнение фигуры».

Определение 1. Уравнением фигуры на плоскости в декартовых координа-

1. цч называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие н ому уравнению, являются координатами некоторой точки фигуры.

[* учебнике JI. С. Атанасяна дается общее понятие «уравнение линии».

Определение 2. Уравнение с двумя переменными х и у называется урав­нением линии Z, если этому уравнению удовлетворяют координаты любой точ­ки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой

МИНИН.

У равнение фигуры на плоскости в общем виде можно записать так:

/ (\, у) 0. Приведем примеры.

239

240