Б. Интеграция аналитического и графического методов в изучении квадратичной функции

Квадратичная функция вводится и изучается в тесной связи с квадрат­ными уравнениями и неравенствами, которые представлены в курсе алгебры 8 класса. Первой из этого класса функций рассматривается функция у = х². Свойства этой функции во многом отличаются от рассмотренного случая ли­нейных функций.

1. Прежде всего, эта функция немонотонна; только на этом этапе у уча­щихся появляется пример функции, отличной от линейных, которые немоно­тонны на всей области определения. Чтобы подчеркнуть указанное отличие, можно предложить учащимся следующее задание: функция задана формулой

у - х² на промежутке -2 < х < 3. Найти множество значений этой функ­ции. Перенося свойство монотонности с класса линейных функций на функцию у = х², учащиеся часто делают ошибку, приводя ответ: промежуток 4 < х < 9. Эта ошибка требует рассмотрения графика функции у - х².

2. Другое отличие состоит в том, что характер изменения значений функции у = х² неравномерный: на одних участках она растет быстрее, на других - медленнее. Эта особенность выявляется при построении графика, причем целесообразно рассмотреть два графика: один - в крупном масшта­бе на промежутке - 1 < х < 1, другой - в мелком масштабе на промежутке

- 3 < х < 3. Построение можно вести методом загущения. Важно отметить свойство параболы - симметричность относительно оси ординат; в дальней­шем это свойство приведет к рассмотрению класса четных функций, причем функция у = х² является ведущим примером функции этого класса.

Рассмотрим более подробно схему изучения квадратичной функции.

1. этап. Изучение данного материала следует начать с рассмотрения кон­кретных ситуаций или задач, приводящих к квадратичной функции.

Вначале необходимо заметить, что в различных областях науки и техники часто встречаются функции, которые называют квадратичными. Приведем примеры.

1. Площадь квадрата у со стороной х вычисляется по формуле у = х².

2. Если тело брошено вверх со скоростью 3, то расстояние s от него до поверхности земли в момент времени t определяется формулой

сг(^

S ⁼ - —— f &t + £q ,

где s₀ - расстояние от тела до поверхности земли в момент времени t = 0.

В этих примерах рассмотрены функции вида у = ах² + Ьх + с. В первом при­мере а~ 1₉Ь = с = 0, а переменными являются х и у. Во втором примере а = - у,

Ъ = 3, с = sо, а переменные обозначены буквами t и

2. этап. На этом этапе формулируется определение квадратичной функции и дается её запись в виде формулы.

142

Определение. Функция у = ах + Ъх + с , где а, Ь и с заданные действи­тельные числа, а * 0, х - действительная переменная,, называется квадратичной функцией.

Затем приводятся примеры квадратичных функций (учителем и уча­

щимися) у

у = -2х , у = х -х, у = х

2 1

• 5х + 6, у = -Зх + - х и т.д. Для

усвоения определения учащиеся выполняют упражнения на распознавание.

3. этап. Ознакомление учащихся с графиком квадратичной функции на- чинается с графика функции у = х². Для построения графика этой функции со- ставляется таблица её значений. Построив указанные в таблице точки и соеди- нив их плавной кривой, учащиеся получают график функции у = х².

4. этап. На этом этапе учащиеся исследуют свойства функции у = х². Ис- пользуя график, они выясняют следующее.

1. Значение функции у - х² положительно при х ф 0, и равно нулю при х = 0. Следовательно, парабола у = х² проходит через начало координат, а ос- тальные точки параболы лежат выше оси абсцисс. Говорят, что парабола у = х² касается оси абсцисс в точке (0; 0).

2. График функции у = х² симметричен относительно оси ординат, так как (-х)² = х². Например, у(-3) = у(3) = 9. Таким образом, ось ординат является осью cwvmempuu параболы. Точку пересечения параболы с её осью симметрии называют вершиной параболы. Для параболы у = х² вершиной является начало координат.

3. При х > 0 большему значению х соответствует большее значение у. На- пример, у (3) > у (2). Говорят, что функция у = х² является возрастающей на промежутке х > 0.

При х < 0 большему значению х соответствует меньшее значение у. Напри- мер, у (-2) <у (-4). Г оворят, что функция у = х² является убывающей на промежутке х < 0 (все рассуждения сопровождаются рассмотрением графика функции).

Следует заметить учащимся, что парабола обладает многими интересными свойствами, которые широко ис- пользуются в технике. Например, на оси симметрии пара- болы есть точка, которую называют фокусом параболы (рис, 44). Если в этой точке находится источник света, то все отраженные от параболы лучи идут параллельно. Это свойство используется при изготовлении прожекторов, локаторов и других приборов.

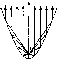
Рис. 44

2 1 Фокусом параболыу = х является точкаF(0; -).

Изучение класса квадратичных функций может проходить в двух вариантах (они достаточно подробно рассмотрены в работе Е.С. Канина «Начала в изучении функций», М.. 2005. Изучите их самостоятельно по приведенному тексту.)

Вариант!

Порядок рассмотрения квадратичной функции и графиков следующий:

1)у = х²; 2) у = ах²; 3 )y-ax²+k;

143

4) У ~ ct(x - т)²; 5) у ~ а(х - т)² + к

Остановимся на этой схеме подробнее.

1. Функция у = ах²,

При изучении этой функции требуется установить роль коэффициента а: при а > О функция имеет минимум, при а < О - максимум в начале координат. При | а | < 1 происходит растяжение параболы от оси ординат (парабола стано­вится более «пологой»), при | а \ > 1 - сжатие к оси ординат (парабола стано­вится «круче»). Все это должно иллюстрироваться конкретными примерами и графиками.

Свойства функции у- ах².

1. Если х - О, то у = 0.

2. Еслих = ±1, то у = а.

3. Если х * 0 и а > 0, то у > 0, если а < 0, то у < 0.

4. Противоположным значениям аргумента соответствуют одинаковые значения функции: ах = а{-х) при любых х.

5. При а > 0 функция возрастает, если х >0, и убывает, если х < 0; при а < 0 - возрастает, если х < 0 и убывает, если х > 0.

6. Если | а | < 1, то график функции у = ах² «сжимается» к оси абсцисс (по сравнению с графиком у = х²); если | а | > 1, то графику = ах² «сжимается» к оси ординат.

Заметим, что свойства 2,3,5 и 6 функции у = ах² зависят от коэффициента а.

2. Функция у = ах + к.

Геометрически к означает здесь ординату точки параболы с абсциссой 0, то есть график функции сдвигается (переносится) вдоль оси ординат на к вверх, если к > 0, и на | к | вниз, если к < 0. Свойства четности функции (сим­метрии графика относительно оси ординат), промежутки её монотонности (в зависимости от знака а) рассматриваются аналогично функции у = ах².

Добавляются и новые свойства квадратичной функции: функция у = ах² имела нуль при х = 0, функция же у = ах² + к может (при к ф 0) иметь два нуля или не иметь ни одного. Это надо показать как аналитически, так и графически: нули функции имеют вид

(при условии, что к и а противоположных знаков). На графике это выглядит так (рис. 45):

Рис. 45

144

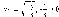
Как видим, если ки а имеют противоположные знаки, то график функции у = ах² + к пересекает ось абсцисс, то есть функция имеет два нуля, если же к и а одинаковых знаков, то график функции не пересекает ось абсцисс, то есть функция не имеет нулей.

Наряду с вопросом о нулях функции возникает и вопрос о промежутках знакопостоянства, который следует рассмотреть подробно, так как он часто ис­пользуется при решении квадратных неравенств.

В случаях, когда а и к одного знака, один и тот же знак имеют и все значе­ния функции. Если а и к отрицательны, то отрицательны и значения функции у = ах² + к Это следствие того, что функция не имеет нулей.

Если же функция имеет два нуля, то имеются промежутки области опре­деления, на которых функция принимает только положительные или только от­рицательные значения. На такие промежутки область определения разбивается нулями функции. Если обозначить нули функции Х\ и х₂, то при а> О и & < О на промежутках (- °о; х₁) и (х₂; + со j функция принимает положительные значе­ния, на промежутке (хь х₂) - отрицательные. При а < О, к > 0 функция положи­тельна на промежутке между своими нулями и отрицательна на промежутках (- оо; Xj) и(х₂; +ooj. Все это хорошо видно на рисунке 45. Все сказанное широ­ко используется при решении квадратных неравенств.

И еще одно свойство. В точке х = 0 функция имеет экстремум равный к: ес­ли а > 0 к- минимум, если а < 0, то к- максимум функции у = ах² + к (рис. 45).

Зс Функция у = а(х - т)².

Геометрически т означает здесь абсциссу точки параболы с ординатой, рав­ной 0. Значит, х ~ т является нулем функции у = а(х - т)². Иными словами, график функции у- ах переносится вдоль оси абсцисс на т. Сам этот факт ус­ваивается учениками достаточно трудно, поэтому необходимо привести кон­кретные примеры, рассмотреть параллельный перенос графика как вправо (при т > 0), так и влево (т < 0) вдоль оси абсцисс.

Как и функция у = ох², функция у = а(х - т)² при а > О возрастает, но уже при х>т, и убывает при х < т. При а < 0, наоборот: при х > т убывает, а при х < т - возрастает.

Кроме того функция, если х ф т₉ при а > 0 положительна, а при а < 0 от­рицательна.

4. Функция у = а(х - т)² + к.

Построение графика этой функции осуществляется последовательным выполнением параллельного переноса графика функции у = ах² вдоль оси абс­цисс на т и вдоль оси ординат на к.

Если в формуле, задающей функцию, раскрыть скобки и привести подоб­ные слагаемые, то функция примет вид

у = ах² + Ьх + с, где Ъ ~ -2ат, с - am² + к, т = -—> к = ———.

2 а 4 а

Таким образом, функция у = ах² + Ьх + с имеет вид

145

t , Ъ _ч2 , 4ac-b² у = ф+—) + —- ₇.

2д 4а

Эта же форма получается путем выделения из трехчлена ах² + Ьх + с полно­го квадрата.

Итак, для построения графика функции у = ах² + Ьх + с достаточно пере­нести график функций у — ах² на вдоль оси абсцисс и на ^4ас ~^Ъ вдоль оси

2 а 4 а

ординат.

Гораздо проще в этом случае перенести не график функции, а систему координат, построив сначала график функции у = ах².

Вариант 2

Рассмотрение квадратичной функции и графиков проходит в следующем порядке:

1 )у = х²; 2) у = ах²; 3)у = а(х~т)²;

4)у = а(х - т)² + к; 5) у = ах² + Ьх + с.

Число шагов от начала изучения квадратичной функции в этом варианте меньше на один, но он имеет и недостатки. В частности здесь фактически выпа­дает изучение параллельного переноса графика функции у = ах вдоль оси орди­нат, поэтому сразу приходится переходить к более сложному переносу того же графика вдоль оси абсцисс. В школах и классах с углубленным изучением мате­матики возможен сразу переход от функции у = ах² к функции у = ах²+ Ьх +с, с

D> О

а > 0, с > О

а > 0, с < О

D> О

Рис. 46

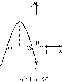
выделением полного квадрата и построением графика функции путем примене­ния двух параллельных переносов.

Следует отметить, что целью изучения квадратичной функции является не только построение графика, но и оценка поведения функции у = ах + Ьх + с, выявление роли коэффициентов а, b, с. Роль коэффициента а уже рассмотрена нами. Геометрический смысл коэффициента с - это ордината точки пересече­ния графика функции с осью Оу.

Нули квадратичной функции связаны со знаком дискриминанта D - Ь² - 4ас: если D = 0, то функция имеет один нуль, равный абсциссе вер­шины параболы х = - (его в алгебре называют двойным или двукратным

нулем); если D > 0, то функция имеет два различных нуля, они находятся по формулам корней квадратного уравнения; если D < 0, то функция действитель­ных нулей не имеет.

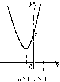
Все сказанное полезно изобразить геометрически: график функции у = ах² + Ьх + с может иметь с осями координат три общих точки, когда D > О (два нуля и точка (0; с) (рис. 46); две общих точки, если D = 0; одну общую с осью ординат точку, если D < 0 (рис. 47). При этом: если а > 0, то функция имеет минимум, если а < 0 - максимум.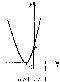

Рис. 47

При D > 0 коэффициенты а и с могут иметь как различные, так и совпа­дающие знаки, а при D < 0 а и с обязательно одного знака.

147

Ордината вершины параболы совпадает со значением максимума (мини-

s. 4 ас-Ъ² мума): у = .

4 а

Промежутки знакопостоянства записываются так же, как и для функции у = ах² + &, но зависят они от знака дискриминанта и коэффициента а: при D > О, а > О положительные значения функция принимает на двух интервалах (-оо; х\) и (х₂; +<*>), отрицательные значения - на интервале (хь х₂). Со сменой знака ко­эффициента а на интервалах слева и справа от нулей квадратичная функция от­рицательна, а на интервале между нулями функции - положительна.

Все сказанное можно иллюстрировать графически (рис. 46,47).

Полезно, как и в случае функции у = ах², показать, как от коэффициента а зависит положение графика функции у = ах² + Ьх + с:

при | а | < 1 график «растягивается» вдоль оси Ох;

при | а | > 1 - «сжимается» вдоль оси Ох (или «сжимается» к оси Оу).

Так будет раскрыт геометрический смысл коэффициентов квадратичной функции.

Большую роль в изучении этой темы играют упражнения. Кроме стан­дартных упражнений, которые представлены в учебниках, здесь полезны зада­ния, предполагающие интеграцию аналитического и графического методов, на­правленные на глубокое усвоение геометрического смысла коэффициентов в формуле, задающей квадратичную функцию, на понимание и сопоставление свойств функций и их графического изображения и наоборот; на формирование у учащихся хорошей привычки анализировать условия, заданные как аналити­чески, так и графически. Приведем некоторые примеры таких упражнений.

1. Может ли парабола на рисунке 48 быть графиком функции:

а)у = ах²-ах + Ь\ б)у = ах + ЪхЛ а\ в)у = ax' - х + а?

2. На рисунке 49 изображен график функции у = х графики функций:

а) у = х² + рх - q; б) у = х² - рх + q\ в) у = -х² +рх + q.

3. Могут ли параболы (рис. 50) быть графиками функций:

~ рх + q. Изобразите

а )Дх) = ах + Ьх + с\ и

б)Дх) = ах² + Ь\ х + с и

в)Дх) = ab х² + х + 1 и

g(x) = Ьх + ах + с₂; g(x) = сх² + Ь₂ х + а; g(x) - ах² + х + Ы

Рис. 49

148

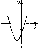
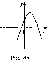
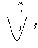
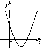
Рис. 50

Следующие упражнения направлены на выяснение положения графика квадратичной функции относительно оси абсцисс.

4. При каких условиях данные параболы касаются оси абсцисс:

я)А^х)^=х2 + ях + 4; б) у =(а- 1)х² + (а + 4)х + а + 7;

в) g(x) = (ах + Ъ) ² + {а\ х + Ъ\)²1

5. При каких действительных значениях а данные параболы расположены:

а) выше оси абсцисс:

1 )у = х² + 2(3а - 1)х + 2а + 1; 2)у = х² - 2(а+ 1)х + а;

б) ниже оси абсцисс:

1 )у = ах² - 2х + а- 1; 2)у = (а- 1)х² + ах~ 1.

Вопросы и задания

1. Подготовьте сообщение об истории возникновения понятия функции и причинах его эволюции.

2. Кто впервые ввел термин «функция»?

3. Почему понятие функции было введено в школьный курс матема­тики? Какие ученые в России и за рубежом выступали за его введение? Как А. Я. Хинчин обосновывал введение понятия функциональной зависимости в школьный курс математики?

4. Какие исторически сложившиеся определения понятия функции су­ществовали в конце XIX - начале XX века?

5. Какие варианты определения понятия функции существуют в на­стоящее время в математике - науке?

6. Какие методические трактовки понятия функции использовались в школьном курсе математики? Назовите достоинства и недостатки каждой из них.

7. Опишите методику введения понятия функции. Какие виды упражне­ний необходимы для формирования этого понятия?

8. По какой схеме происходит изучение функций в курсе алгебры основ­ной школы? Проиллюстрируйте сказанное на конкретном примере.

9. Как вводится понятие графика функции? Приведите пример. Каков ал­горитм построения графика функции?

10. Какие упражнения необходимы для формирования умения «читать» график функции? Приведите примеры.

149

11. Опишите методику введения понятия линейной функции и её графика. Какие частные случаи линейной функции изучаются в курсе алгебры 7 класса?

12. Что геометрически означают коэффициенты Ъ и к в формуле у = /Ьс + 6?

13. Какие умения формируются у учащихся при изучении линейной функции?

14. Составьте упражнения на усвоение учащимися взаимного расположе­ния графиков линейных функций.

15. В чем отличие свойств квадратичной функции от свойств линейной функции?

16. Охарактеризуйте этапы изучения квадратичной функции.

17. Проанализируйте действующие учебники алгебры для 8 класса. В каком порядке проходит изучение класса квадратичных функций в каждом из них?

18. Как реализуется интеграция алгебраического и графического методов при изучении квадратичной функции? Приведите соответствующие примеры.

19. Разработайте методику введения одной из следующих функций (на выбор): 1) степенной; 2) показательной; 3) логарифмической; 4) тригономет­рических; 5) обратных тригонометрических. Составьте общую схему изучения этих функций.

Рекомендуемая литература

1. В и л е н к и н, Н. Я. Функции в природе и технике / Н. Я. Виленкин. - М.: Просвещение, 1985.

2. В о л ь х и н а, И. Н. Дифференцированные задания по темам «Функции» и «Рациональные дро­би» / И. Н. Вольхина // Математика в школе. -1999. - № 1. - С. 9 -13.

3. Дворянинов, С. В.₅ Розо в, Н. X, некоторые замечания об изучении функции в школе /

С. В, Дворянинов, Н. X. Розов // Математика в школе. -1994. - № 5. - С. 27 - 30.

4. К а н и н, Е. Начала в изучении функций / Е. Канин. - М.: чистые пруды. 2005. - 32 с.

5. К л е й н, Ф. Элементарная математика с точки зрения высшей. Т. 1. - M.-JL, 1933.

6. К о л я г и н, Ю. М. Методика преподавания математики в средней школе. Частные мето­дики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов / Ю.М. Колягин, F.JI.

Луканкин, E.JI. Мокрушин и др.. - М.: Просвещение, 1977.

7. М а р н я н с к и й, И. А. Ещё раз об определении функции / И. А, Марнянский // Математика в школе. -1991. -№4. - С. 71 -72.

8. Методика преподавания математики в средней школе: Частная методика: Учеб. посо­бие для студентов пед. ин-тов по физ.-мат. спец. /А.Я. Блох, В.А. Гусев, Г.В. Дорофеев и др.; Сост. В.И. Мишин. - М.: Просвещение, 1987.

9. С а р а н ц е в, Г. И. Упражнения в обучении математике / Г. И. Саранцев. - 2-е изд., дораб. - М.: просвещение, 2005. -255 с.

10. Теляковский, С. А. О понятии функции в школьном курсе математики / С. А. Теля- ковский // Математика в школе. -1989. - № 4. - С. 90 - 91.

И. X и н ч и н, А. Я. Основные понятия математики и математические определения в средней школе / А. Я. Хинчин. - Учпедгиз, 1940.

12. X и н ч и н, А. Я. Педагогические статьи./ А. Я. Хинчин. Под ред. Б. В. Гнеденко. - М.. 1963. - 204 с.

13. Ц у к а р ь, А. Я. Изучение функций в VII классе с помощью средств образного характера / А. Я. Цукарь // Математика в школе. - 2000. - № 4. - С. 20 - 27.

14. Школьные учебники алгебры для 7-9 классов.

15. http ://wM.km-school.ru/wiki/index.plip/

150