По этому учебнику предлагается решать некоторые задачи на проценты с помощью уравнений. Эти рекомендации относятся к двум видам задач: нахож­дение числа по данному числу его процентов и нахождение процентного отно­шения двух чисел. Примеры этих задач и образцы их решения мы рассмотрим на практических занятиях.

В 6 классе изучаются две основные задачи на дроби: а) нахождение дроби числа; б) нахождение числа по данному значению его дроби. Основным спосо­бом решения этих задач является способ приведения к единице, выраженный правилами:

• чтобы найти дробь от числа, нужно число умножить на эту дробь;

• чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.

Решение задач с помощью пропорций в 6 классе предусматривает ис­пользование понятий «прямая пропорциональность» или «обратная пропорцио­нальность». Поэтому необходимо учить учащихся кратко записывать условно задачи так, чтобы соответствующие однородные величины записывались стол биком друг под другом. Это позволит учащимся увидеть, какие отношения ка­ждой пары положительных чисел равны.

В целом у учащихся 5-6-х классов должны быть сформированы умения составлять числовые и буквенные выражения, пропорции, линейные уравнения по условиям текстовых задач, решать задачи с помощью арифметических приемов (способов) и уравнений.

Любая текстовая задача, сводящаяся к уравнению первой степени, может быть решена арифметическим способом. Поэтому сопоставление арифметичо ского и алгебраического способов решения текстовых задач в процессе форм и рования умений решать эти задачи будет способствовать повышению интереса учащихся к решению задач, а также накоплению ими опыта самостоятельного поиска решений.

3. Этапы решения задач на составление уравнений и их реализация

В методике математики общепринято следующее деление процесса ре­шения задач: 1) анализ текста задачи; 2) поиск способа решения задачи и со­ставление плана решения; 3) осуществление найденного плана; 4) изучение (анализ) найденного решения.

Выделенные этапы представляют норму деятельности человека по ретс нию задач. Однако в реальном процессе решения необязательно явным образом проходить через все указанные этапы. Это зависит от того, насколько решаю щему известен способ решения задачи. Каждый этап имеет свои признаки (ори> ентиры), руководствуясь которыми учитель формирует у учащихся компоненты общего умения решать задачи.

На первом этапе учитель должен добиться того, чтобы учащиеся «при няли» задачу, то есть поняли её смысл, сделав целью своей деятельности. И

itom случае задача становится объектом мышления. Поэтому усвоение текста пэдачи учащимися будет первой важной целью учителя.

Исходным здесь является выделеше в задаче условия, то есть данных и отношений между ними, и требоватя задачи, то есть искомого (искомых) и отношений между ними. Затем выявляется в задаче основное отношение, на­правляющее процесс поиска решения. Это отношение обычно имеет вид функ­циональной зависимости двух типов: а • b = с и а\ + а^ = а^

Важное значение на этом этапе имеют краткая запись текста задачи, со­ставление схем, рисунков. Схемы и рисунки выступают в роли наглядного представления содержания задачи и зависимостей величин, входящих в неё. Гщб большее значение приобретает схема в pom модели, выявляющей скрытые шисимости между величинами. Поэтому составлению кратких записей и схем но тексту задачи необходимо специально обучать.

На первом этапе решения необходимо также актуализировать «базис» Iшшения задачи, то есть теоретическую и практическую основу, необходимую для обоснования решения. Здесь же выясняется, не принадлежит ли задача к и звестному типу задач.

На втором этапе процесса решения задачи выясняется стратегия решения:

1. устанавливается, будет ли неизвестным, относительно которого со- г п шляется уравнение, искомая величина или же промежуточная величина (если находят сначала промежуточную величину, то искомая величина выражается через неё);

2. выясняется, для каких величин соответствующие выражения будут приравниваться.

Затем осуществляется поиск способа решения задачи на основе построе­нии модели поиска. Аналитико-синтетический поиск решения заканчивается получением уравнения. Соответствующий план решения обсуждается с учащи­мися, при этом используется табличная запись поиска решения задачи. Иногда и пап как способ решения задачи оформляется письменно. В этом он выполняет роль ориентировочной основы деятельности учащегося.

На третьем этапе осуществляется найденный план решения, выполня- г гея проверка решения и записывается полученный ответ.

Четвертый этап - изучение (анализ) найденного решения задачи. На этом этапе выделяется главная идея решения, существенные его моменты, про­исходит обобщение решения задач данного типа. Выясняются недостатки ре­шения и производится поиск другого, более рационального решения, выявляются и закрепляются в памяти учащихся приемы, которые были использованы в про­цессе решения задачи. Перед учащимися ставятся вопросы:

1. Какова главная идея решения данной задачи?

2. Нельзя ли указать другие способы решения данной задачи? ■

3. Почему рассмотренный способ решения является рациональным? И т.д.

Формы записи решения

1. Развернутая, когда решение оформляется в виде связного рассказа.

2. Запись-перечень, когда дается перечень величин, выраженных через

113

Количество зерна, т	I элеватор	II элеватор
Сначала	?	?
Потом	? - 750	? + 350

этап (поиск способа решения задачи и составление плана решения). Здесь обсуждается стратегия решения. Затем вводится обозначение иско­мой или другой неизвестной величины в зависимости от стратегии. Пусть х т - количество зерна, которое было во втором элеваторе, тогда модель поиска решения задачи в виде таблицы примет вид: Таблица 3 Количество зерна, т	I элеватор	II элеватор
Сначала	2х	X
Потом	г <^Г\ о	х + 350

2. этап (осуществление найденного плана решения). После построения таблицы 2 делаем пояснение:

Так как в задаче сказано, что в обоих элеваторах зерна стало поровну, то можно составить уравнение:

2х- 750 =х + 350, х = 1100.

О т в е т: в I элеваторе было 2200 т, во II элеваторе -1100т.

114

3. этап (изучение (анализ) найденного решения). На этом этапе можно решить данную задачу с помощью линейной диаграммы. Проиллюстрируем, как реализуются этапы решения задачи в этом случае.

1. этап (построение линейной диаграммы). После прочтения текста задачи обсуждаются следующие вопросы (самими учащимися или с помощью учителя):

1. Сколько ситуаций рассматривается в задаче? (Две: первоначальная и конечная.)

2. С какой ситуации следует начать построение линейной диаграммы? (Можно начать построение с первой ситуации и от неё перейти ко второй, а можно сначала построить линейную диаграмму конечной ситуации и перейти от неё к первоначальной. Рассмотрим первый вариант построения линейной диаграммы.)

3. Что будет представлять собой линейная диаграмма первоначальной си­туации? (Два отрезка, один из которых в 2 раза больше другого. Первый отрезок будет изображать количество зерна в первом элеваторе, а второй - во втором.)

После этого учащиеся строят диаграмму первоначальной ситуации. Затем рассуждения продолжаются.

4. Как перейти на диаграмме от первой ситуации ко второй? (Надо из первого отрезка вычесть отрезок, условно изображающий 750 т, а ко второму отрезку прибавить отрезок, изображающий 350 т.)

5. Произвольно ли берутся эти отрезки? (Нет, следует учитывать, что ниовь полученные отрезки должны быть равны, так как на обоих элеваторах черна стало поровну.)

Выполнив действия с отрезками, учащиеся получают диаграмму конеч­ной ситуации. Первый этап работы над задачей заканчивается обозначением Отрезков и оформлением записей на чертеже.

2. этап (решение получившейся геометрической задачи.)

Построенная линейная диаграмма превращает алгебраическую задачу в

геометрическую, решение которой основано на использовании свойств длины отрезка, а именно: 1) равные отрезки имеют равные длины; меньший отрезок имеет меньшую длину; 2) если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков.

Решение учащиеся записывают на геометрическом языке, используя обо- тимения отрезков, а результат переводят на естественный язык. В данном слу­чае этот перевод осуществляется автоматически за счет переноса терминологии < III этап). Вначале следует делать подробную запись решения с указанием To­rn, что изображает каждый отрезок. Постепенно можно переходить к краткой «и шеи, так как некоторые факты видны на чертеже.

Приведем подробную запись решения задачи 1.

Решение

1. этап. Пусть отрезок АВ изображает количество зерна в первом элева- ТОре (рис. 32), тогда отрезок CD (CD = ~ АВ) будет изображать количество зер­ня но втором элеваторе.

115

АВ = 2 CD - первоначальное распределение зерна между элеваторами. Из первого элеватора вывезли 750 т зерна, а на второй элеватор привезли 350 т, поэтому вычтем из отрезка АВ отрезок ВК, условно изображающий 750 т, а к отрезку CD прибавим отрезок DE, изображающий 350 т. (Отрезки ВК и DE бе­рем не произвольно, а такие, чтобы отрезки АК и СЕ были равны.)

АК= СЕ - конечное распределение зерна между элеваторами.

II этап. 1 способ. CD = = FB (по построению), FB = jFX + ХБ - =350 + 750 = 1100, значит, CD= 1100,^#= 1100 • 2 = 2200.

О т в е т: в первом элеваторе было 2200 т зерна, во втором - 1100 т.

Учащиеся могут делать краткую запись решения задачи, например, она может быть такой:

Решение

АВ = 2CD - первоначальное распределение зерна между двумя элеватора,- ми.АВ-ВК = АК, CD + DE = СЕ,

АК = СЕ -конечное распределение зерна между элеваторами.

CD = AF = FB (по построению), FB = FK + КВ, FB = 350 + 750 = 1100, тогда CD= 1100, ЛЯ = 1100 ■ 2 = 2200.

Ответ: 2200 т, 1100 т.

Как видим, в данном случае ответ получили, не составляя уравнение.

Необходимо заметить, что диаграмма позволяет составить не только арифметическое выражение, но и различные уравнения к задаче, которые уча­щиеся не могут записать без чертежа. Таким образом, появляется возможность решить задачу алгебраически несколькими способами.

Приведем краткую запись других способов решения задачи 1.

2. способ. Пусть АК = СЕ = х, тогда, так как АВ = 2CD, получим:

х + 750 = 2(х- 350), откуда х = 1450, CD = 1450 - 350 = 1000, АВ = 1100 • 2 = 2200.

Ответ: 2200 т, 1100 т.

2. способ. Пусть CD = х, тогда АВ = 2х. Так как АК = СЕ, то имеем:

2х- 750 = х + 350.

(такое же уравнение получается при решении задачи без диаграммы.)

3 а д а ч я 2 (основное отношение а ■ Ъ = с). По плану бригада должна была выполнить заказ за 10 дней. Но фактически она перевыполняла норму на 27 деталей в день и за 7 дней работы не только выполнила предусмотренное планом задание, но и изготовила сверх плана 54 детали. Сколько деталей в день должна была изготовлять бригада по плану?

Величины	По плану	Фактически
11роизводительность бригады, дет. в день	?	? на 27
Время работы, дн.	10	7
< )бъем выполненной работы	?	? на 54

этап (поиск способа решения). Учащиеся выясняют здесь основное отношение: V = р • t, обозначают через х искомую величину и составляют мо­дель поиска решения в виде таблицы 5. Таблица 5 Величины	По плану	Фактически
I! роизводительность бригады, дет. в день (р)	X	х +27 на 27
Время работы, дн. (tp)	10	7
()бъем выполненной работы (Ур)	10х	(х + 27) • 7 на 54

2. этап (осуществление плана решения)

Так как по условию задачи бригада за 7 дней работы не только выполнила Здание, но и изготовила сверх плана 54 детали, то можно составить уравнение:

10х + 54 = (х + 27) • 7,

10* + 54 = 7х+ 189,

Зх = 135, х = 45.

Решение задачи не может заканчиваться решением уравнения: необходимо проверить, удовлетворяет ли полученный корень уравнения условию и требованию щачи, то есть необходимо сделать проверку корня уравнения по смыслу задачи.

Проверка х = 45 - положительное число, х + 27 = 45 + 27 = 72 - положительное число,

(х + 27) • 7 = 72 • 7 = 504 - положительное число,

1. Ох = 10 * 45 = 450 - положительное число,

117

504 - 450 = 54 - положительное число, являющееся данным.

Следовательно, х = 45 удовлетворяет условию задачи, то есть является её решением.

Ответ: бригада должна была изготовлять в день по плану 45 деталей.

IV этап (изучение и анализ найденного решения). На этом этапе можно решить с учащимися задачу геометрическим методом с помощью двумерной диаграммы. Двумерная диаграмма может состоять из площади одного или не­скольких прямоугольников (параллелограммов, треугольников, трапеций).

Решение

D С

Рис. 33

Пусть отрезок АВ изображает производительность бригады в день по пла­ну (рис. 33). AD - срок выполнения заказа по плану, тогда Sabcd определяет весь заказ по выпуску деталей.

AM изображает количество деталей, которое выпускала бригада ежедневно,

АР - срок выполнения заказа, тогда Samnp соответствует количеству деталей, которое выпустила бригада за 7 дней.

По условию задачи бригада выпустила сверх плана 54 детали, поэтому имеем:

Si + S₃ + 54 = S₃ + S₂ или S\ + 54 = S₂, но S₂ = 27 ■ 7 = 189, поэтому

iSj + 54 = 189, откуда S\ = 135.

С другой стороны, Si = ЗАВ, поэтому ЗАВ =135, тогда АВ = 45.

Ответ: бригада должна была изготовлять в день по плану 45 деталей.

(Подробно об использовании двумерных диаграмм при решении тексто­вых задач см. в работе [4].)

Одно из преимуществ геометрического метода состоит в наглядности.

Построение двумерной (или линейной) диаграммы и переход от одного её состояния к другому делает более осязаемым процесс, описываемый в задаче, и тем самым позволяет лучше понять её.

При решении задачи геометрическим методом учащиеся могут опираться на чертеж, использовать геометрические знания и умения. Иногда они могут решить задачу, даже не составляя уравнение, ответ бывает виден на чертеже. Геометрический метод решения задачи можно использовать в качестве провер­ки решения, полученного без чертежа, чисто алгебраически. (Более подробно о

118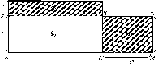

Величины	_ I	Размеры площадки II
Ширина, м	X		х + 4 на 4
Длина, м	840 X		840 — на 5 х + 4
Площадь, м2	840		840

Уравнение 840 х - 5 = 840 х + в данном случае получается путем сравнения двух выражений одной и той же величины (длины), являющейся вторым ком­понентом основного отношения а* Ь = с. При том же выбранном неизвестном уравнение можно составить путем сравнения двух выражений другой величины - площади, являющейся третьим компонентом основного отношения а • Ъ = с. Таблица 7 Величины		I	Размеры площадки II
Ширина, м		X		х + 4 на 4
Длина, м	840 X			840 . . 5 на 5 X
Площадь, м2		840		(М_5Хх + 4) X

,840

Уравнение будет иметь вид; 840 = (_ - 5)(* + 4).

х

Возможен и третий путь Поиска решения. Если через х м обозначить ши­рину площадки, а через у м её длину, то модель поиска решения задачи приве­дет к системе уравнений:

119

j xy = 840,

{(x + 4)(y - 5) = 840.

Эту же задачу можно решить и геометрическим методом с помощью двумерной диаграммы. Причем, геометрическая модель её будет иметь такой же вид, как и в задаче 2, только, в отличие от первого случая, площади S\ и Si будут равны. (Решите задачу геометрическим методом самостоятельно!)

Большие возможности в решении текстовых задач геометрическим мето­дом представляет использование графиков равномерных процессов. Метод ре­шения в этом случае называется графико-геометрическим. Приведем примеры.

Задача 4. С двух аэродромов навстречу друг другу вылетели одно­временно два самолёта. К моменту встречи первый пролетел на 200 км больше второго. Остальной путь до аэродрома первый пролетел за 5/3 часа, а второй за 12/5 часа. Найти расстояние между аэродромами.

L Алгебраический метод решения задачи (без чертежа) приводит к сис­теме уравнений:

^5х _ 12у 3 у 5х 12 5

— v--x = 200,

15 3

где х км/ч - скорость первого самолета, у км/ч - скорость второго самолета.

II. Решим задачу графико-геометрическим методом.

Рассмотрим две прямоугольные системы координат хОу и х О у (рис. 34),

Рис. 34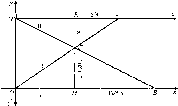

Ох и Ох - оси времени с одинаковыми масштабами. Отрезок 00 изо­бражает расстояние между аэродромами.

Так как движение равномерное, то отрезок О А - график движения пер­вого самолёта. Второй самолет движется навстречу первому, поэтому отре­зок ОЪ - график движения второго самолёта. Пересечение графиков в точке С соответствует моменту встречи самолетов.

120

Обозначим через х км путь, который пролетел второй самолет до встречи, тогда (х + 200) км пролетел до встречи первый самолет.

Рассмотрим две пары треугольников:

А ОМС ~ ААКС (по первому признаку), тогда:

3t х + 200

т⁼—•

АВМС ~ АО КС (по первому признаку), тогда:

12 х + 200

— = . (2)

51 х

Из равенств (1) и (2) получаем:

3/12 ₂ „

у , откуда t =4,

тогда t = 2 (отрицательный корень уравнения не удовлетворяет условию зада- чи). Подставив полученное значение t в (1), получим:

6 х + 200 5 ~ х ’

решая это уравнение, находим: х = 1000, тогда х + 200 = 1000 + 200 - 1200.

Всё расстояние S = 1000 + 1200 = 2200 (км).

Ответ: 2200 км.

Аналогично решаются задачи на совместную работу.

Задача 5. Двое рабочих, выполняя задание вместе, могли бы закон­чить его за 12 дней. Если сначала будет работать только один из них, а когда он выполнит половину всей работы, его сменит второй рабочий, то все зада­ние будет закончено за 25 дней. За сколько дней каждый рабочий в отдельно­сти может выполнить все задание?

1. Алгебраический метод решения задачи (без чертежа) приводит к урав­нению:

1 1 1

12 х 50-х

где х - количество дней, за которое первый рабочий выполнит все задание.

2. Решим задачу графико-геометрическим методом.

Построим графическую модель задачи (рис. 35). Для определенности предположим, что первый рабочий работает быстрее, чем второй. Так как в •додаче работа рассматривается как равномерный процесс, то отрезок AN - график работы первого рабочего, а отрезок BD - график работы второго ра- бочего. AQ - изображает время совместной работы. AQ = 12.

Проведем NK \\BD, тогда АК =50. Затем используем подобие образо- вавшихся треугольников.

ANMA ~ АР КА ~ APCN, отсюда следует, что = ^{12 + х} . (3)

СР х

ANMK ~ APQD ~ АРСВ, отсюда следует, что ~ • (4)

121