- •Цели, содержание и структура курса математики 5-6 классов
- •Значение и место учения о числе в курсе математики общеобразовательной школы
- •5 Класс
- •6 Класс
- •3. Различные пути расширения понятия числа
- •4. Методика изучения натуральных чисел
- •4. Методика изучения натуральных чисел
- •5. Основные вопросы методики изучения дробей
- •5. Основные вопросы методики изучения дробей
- •6. Методика изучения положительных и отрицательных чисел
- •I. Основные типы преобразований и этапы их изучения
- •III этап. Организация целостной системы преобразований (синтез).
- •Буквенной части слагаемых пока остается первой.
- •1. Содержание и роль линии уравнений и неравенств в современном школьном курсе математики
- •2. Основные понятия линии уравнений и неравенств
- •I * hi лаже он и возникает по ходу обсуждения процесса решения, то ответ на не-
- •Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
- •* Последовательность изучения линии уравнений и неравенств
- •I )гапы изучения линии уравнений, неравенств и их систем в основной школе
- •1* Курсе математики 5 класса понятие уравнения трактуется аналогично.
- •Основные классы неравенств изучаются сразу вслед за изучением со- »»I мотствующих классов уравнений.
- •I Ъшить уравнение - это значит найти все его корни или установить, что их нет.
- •Решение квадратных уравнений и неравенств
- •Il Графический метод (I способ)
- •Графический метод
- •Системы уравнений с двумя переменными, в которых одно или оба уравнения второй степени
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Il Графический метод
- •Il Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •1. Цели обучения решению текстовых задач
- •2. Пропедевтика алгебраического и геометрического методов решения текстовых задач
- •3. Этапы решения задач на составление уравнений и их реализация
- •Этап {перевод задачи на геометрический язык).
- •Этап (решение задачи на геометрическом языке).
- •1. Из истории введения понятия функциональной зависимости в школьный курс математики
- •2. Различные трактовки понятия функции
- •3. Методика введения понятия функции
- •Этап. Мотивация введетя понятия.
- •Исследовать функцию на основные свойства.
- •Использовать изученные свойства функций при решении различных задач, в частности уравнений и неравенств.
- •Влияние коэффициентов hub на поведение функции
- •Взаимное расположение графиков линейных функции
- •Б. Интеграция аналитического и графического методов в изучении квадратичной функции
- •1. Цели и задачи курса геометрии основной школы
- •2. Содержание обучения геометрии в 7-9 классах
- •3. Логические основы изложения геометрии в 7-9 классах
- •Аксиомы принадлежности
- •Аксиомы порядка
- •Аксиомы измерения отрезков и углов
- •Рекомендуемая литература
- •1. Методика изучения основных свойств простейших геометрических фигур
- •1. Учебник а. В. Погорелова: § 1 «Основные свойства простейших геометрических фигур»,
- •Определения «через ближайший род и видовые отличия»
- •Измерение отрезков и углов
- •3. Учебник а. Д. Александрова и др,: глава I «Начала геометрииж
- •2. Методика формирования геометрических понятий
- •3, Обучение решению задач на первых уроках геометрии
- •II группа
- •1. Различные подходы к формированию понятия равенства фигур
- •Что нужно знать, чтобы утверждать равенство треугольников abc и dek1
- •На рисунке 55 изображено два равных треуголь- ника. Написать равенство этих треугольников, обозначив их вершины.
- •Если разносторонние треугольники abc и dkm
- •11Ри иодом пример.
- •I (сн тральное место в изучении равных треугольников занимают признаём риионота треугольников.
- •Доказательство:
- •Доказательство:
- •Треугольники вас и cdb равны. Напишите все соотношения, из ко- торых следует равенство указанных треугольников.
- •Напишите соотношение между элемен- тами треугольников abc и adc, из которых следовало бы их равенство.
- •Какие методические подходы существуют к введению понятия ранено гва фигур в школьном курсе геометрии? Какой подход, на Ваш взгляд, милмется наиболее удачным?
- •В чем особенности введения понятия равных треугольников в разных учебниках геометрии?
- •Приведите примеры упражнений на усвоение понятия равных треугольников.
- •I. Цели и этапы изучения взаимного расположения прямых на плоскости
- •1 Различные подходы к введению понятия параллельности прямых на плоскости.
- •I. Методика изучения признаков параллельности прямых.
- •1, Цели и этапы изучения взаимного расположения прямых на плоскости
- •2. Различные подходы к введению понятия параллельности прямых на плоскости
- •4. Методические замечания к изучению перпендикулярности прямых на плоскости
- •В данной плоскости через точку вне данной прямой можно провести только одну прямую, параллельную данной.
- •Сумма внутренних углов треугольника равна 2d.
- •1. Различные подходы к изучению многоугольников
- •2. Методика изучения четырехугольников
- •Если в четырехугольнике противоположные стороны попарно равны,
- •Если в четырехугольнике диагонали пересекаются и точкой пересечении делятся пополам, то этот четырехугольник параллелограмм.
- •Какие из систем неравенств задают на плоскости трапецию и почему? Покажите штриховкой множество точек плоскости, заданное системой неравенств:
- •1 H найти площадь трапеции.
- •1, Имеет1 ли ось симметрии фигура, заданная системой неравенств:
- •Верно ли утверждение: а) любой правильный многоугольник является выпуклым; б) любой выпуклый многоугольник является правильным?
- •Чему равны градусные меры углов: а) правильного пятиугольника; б) правильного двенадцатиугольника; в) правильного тридцатишестиугольника?
- •Множество направленных отрезков плоскости.
- •Множество классов направленных отрезков плоскости.
- •Множество параллельных переносов плоскости.
- •Начертите равнобочную трапецию: а) существуют ли векторы, определяемые её вершинами и равные по длине? б) Сколько пар сонаправленных векторов задают вершины трапеции?
- •Сколько пар сонаправленных (противоположно направленных) векторов определяют вершины параллелограмма?
- •Начертить параллелограмм, обозна- чить его вершины и написать все равные ме- жду собой векторы, началом и концом кото- рых являются вершины параллелограмма.
- •Векторы а и ъ равны, что следует из этого?
- •3. Методика изучения действий с векторами
- •II. Умножение вектора на число
- •Учебник геометрии а. В. Погорелова.
- •Учебник геометрии j1. С. Атанасяна и Др.
- •Построить вектор, представляющий сумму
- •4. Методика обучения решению задач с помощью векторов
- •1. Дан многоугольник abcde. Представьте ad в виде суммы: а) двух; б) I рёх; в) четырех векторов, заданных вершинами этого многоугольника.
- •Представьте вектор ав в виде суммы векторов ас, dc , bd .
- •Вектор cDколлинеарен вектору ав и Выразите один век-
- •Четырехугольник abcd - квадрат. Упростите выражение { ав - 3 вс)2,
- •VI. Упражнения на нахождение длины вектора и величины угла между векторами.
- •Какие действия с векторами изучаются в школьном курсе геометрии?
- •Б) в треугольнике лвс известны длины всех сторон. Определить его углы.
- •II кн. До н. Э.) уже фактически пользовался прямоугольными координатами.
- •Простейшие задачи в координатах на плоскости
- •Уравнения фигур на плоскости
- •4. Особенности применения метода координат
- •5. Методика формирования координатного метода решения задач
- •Решение (координатный метод)
- •Iэтап(оптимальный выбор прямоугольной системы координат). Выберем прямоугольную систему координат так, как показано на рис. 93.
- •Этап (перевод задачи на координатный
- •Так как м середина стороны вс, то л/
- •Этап (решение задачи на координат- ном языке).
- •Рекомендуемая литература
- •Значение тригонометрических функций в школьном курсе математики и различные подходы к их изложению
- •I ермипы «косинус», «котангенс» и др. Появились в XI—XVII вв.
- •Этапы изучения линии уравнений, неравенств и их систем в
- •Системы уравнений с двумя переменными, в которых
- •Цели и этапы изучения взаимного расположения прямых на
- •Различные подходы к введению понятии параллельности пря
В
отличие от алгебраического, графический
метод решения наглядно
показывает
количество корней, их знаки и позволяет
учащимся избежать воз-
можных ошибок.
В данном случае он может применяться
для проверки отве-
та, полученного
аналитически.
Построим
в одной системе координат
графики
функций (рис. 15)
Vi
=
4д/хн-1
иу2-\
2х-1|
+3.
Построение
графиков можно осуществлять
путем
их преобразований, например, график
первой
функции^! строим по цепочке:
у
=
д/х ->/ - л/хП
—>У1=
4д/х + 1,
а
функции^ “ по цепочке:
у-
(2х-
1)
—» у'
= I
2х-1|
—»
У2
-
I
2х-1|
+3.
Из
рисунка найдем абсциссы точек
пересечения
графиков функций: х\
= 0,х2-
3.
О т
в е т: х\
= 0, х2
= 3.
Сами
корни уравнения при графическом методе
можно находить иногда аналитически,
определив по рисунку промежутки, в
которых они находятся. Это позволит
получить более точный результат в
случае, если корни являются дробными
числами.
Решая
уравнения, содержащие степень, можно
решать и соответствующие им
неравенства. Приведем пример.
Пример13.
Решить уравнение х
и
соответствующие ему нера-
3^5
их
< .
венствах
>-
X X
Решение./.
Алгебраический
метод
Найдем
ОДЗ: х Ф
0.
Умножив
обе части уравнения на х, получим: х4
ние
не имеет корней, т.к. х4
>
0
при любом X.
:
-5. Данное уравне-
Решим
неравенство х > —. Преобразуя данное
неравенство, получим: х
х
+ - > 0
или
X
х
+ 5
>
0,
откуда х > 0.
Аналогично,
решая неравенство х < —, получим х <
0.
х
Построим
в одной системе координат графики
функций уi
=
х3
и у2
=
~-
X
(рис.
16). Из рисунка видно, что графики функций
не имеют точек пересече
ния,
значит, уравнение х'
неравенства.
.з
_
не
имеет корней. Решаем соответствующие
х
87
Графический метод

Графический метод
5
График
функции y\
= x3
расположен
выше графика функции у2
= --
х
1
5
при
х
> О, значит, неравенство х
> —
х
выполняется
при х
>
0. Аналогично, по рисунку видим, что
график функции
-5
у\
-
х3
расположен ниже графика функции^ “
при х < 0.
Рис.
16
Таким
образом, графический метод подтверждает
отсутствие корней у дан
ного
уравнения и наглядно показывает решения
соответствующих неравенств. Учащиеся,
сопоставляя оба метода решения, приходят
к выводу:
L
Если
уравнение, содержащее степень,
не
имеет корней, то геометрически это
означает, что графики функций, стоящих
в левой и правой частях уравнения,
не имеют общих точек, т.е. не пересекаются
и не совпадают. Верно и обратное: если
графики функций, стоящих в левой и
правой частях уравнения, содержащего
степень, не имеют общих точек, то данное
уравнение не имеет корней.
Среди
уравнений, содержащих степень, часто
встречаются такие, в которых переменная
содержится под знаком радикала, то есть
входит в подкоренное выражение.
Такие уравнения называются иррациональными.
Одно из таких уравнений мы уже рассмотрели
в примере 12. Так как интеграция
алгебраического и графического
методов при решении иррациональных
уравнений и неравенств имеет особое
значение, то рассмотрим этот вид
уравнений и неравенств подробнее.
Мотивацию
введения понятия иррационального
уравнения можно провести путем
решения задачи.
Задача.
В
треугольнике ABC
(рис.
51) BD
перпендикулярно
AC,
AD
=
2
см, DC
=
5
см, АВ
+ ВС
= 9
см. Найти BD.
такое
уравнение называется иррациональным,
затем формулируется определение самими
учащимися или учителем.
Определение♦
Уравнение,
в котором переменная входит в какое-либо
выражение, стоящее под знаком корня,
называется иррациональным.
Мы
не будем подробно останавливаться на
алгебраических методах
Решение.
Пусть
длина отрезка BD
равна
х см.
По
условию задачи
5
Рис.
17
Учащиеся
видят, что получилось уравнение, в
котором, переменная входит в подкоренное
выражение. Вводится термин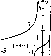
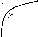
-t—I i'-+В
Тогда
АВ = л]х2+4
и ВС
= /х2
+ 25 .А
2 DС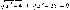
решения
иррациональных уравнений, так как они
описаны в учебниках и учебных пособиях
для учащихся и абитуриентов, а ограничимся
лишь их перечислением: 1)
метод введения вспомогательных
переменных, в результате чего решение
иррационального уравнения сводится к
решению систем уравнений, уже не
содержащих радикалов; 2)
метод изолирования (уединения) радикала
и возведения обеих частей уравнения в
степень, в результате чего приходим к
уравнению, не содержащему радикалов
или содержащему их меньшее число; 3)
метод умножения обеих частей уравнения
на выражение, сопряженное одной из его
частей, и использования свойств
монотонности функций.
Наиболее
часто в школьной практике используется
второй метод.
Следует
заметить, что решение иррациональных
уравнений и неравенств имеет свои
особенности (опасности), в отличие от
ранее рассмотрен- ных видов уравнений
и неравенств, заключающиеся в том, что
в ходе выполнения преобразований
данного уравнения может быть появление
посторонних корней или потеря корней.
Поэтому необходима постоянная проверка
полученных результатов и контроль
выполняемых действий. Здесь интеграция
алгебраического и геометрического
(графического) методов в виде их сочетания
или единства в одном методе не только
желательна, но и необходима. Приведем
примеры.
Пример
14. Решить уравнение yjl-x
=
х и соответствующие ему неравенства
д/ 1
-х
> х и д/ 1-х
<х.
Решение./.
Алгебраический
метод
А) Решим
сначала уравнение д/l
-
х = х.
L
Найдем
ОДЗ:
Сравним
полученные результаты с ОДЗ. Как видим,
х2
< 0, поэтому он является посторонним
корнем.
Б)
Решим неравенство д/l
-
х > х.
Данное
неравенство равносильно совокупности
двух систем рациональных неравенств:
1
- х > О, х > О,
откуда
0
< х < 1.
Возведем
обе части уравнения в квадрат:
-
х = х2.
Решим
полученное уравнение:
2
, 1
л ”1 + J~5
х
+ х - 1
= 0,
откуда Xi
= —,
х2
=
2
89