
- •Цели, содержание и структура курса математики 5-6 классов
- •Значение и место учения о числе в курсе математики общеобразовательной школы
- •5 Класс
- •6 Класс
- •3. Различные пути расширения понятия числа
- •4. Методика изучения натуральных чисел
- •4. Методика изучения натуральных чисел
- •5. Основные вопросы методики изучения дробей
- •5. Основные вопросы методики изучения дробей
- •6. Методика изучения положительных и отрицательных чисел
- •I. Основные типы преобразований и этапы их изучения
- •III этап. Организация целостной системы преобразований (синтез).
- •Буквенной части слагаемых пока остается первой.
- •1. Содержание и роль линии уравнений и неравенств в современном школьном курсе математики
- •2. Основные понятия линии уравнений и неравенств
- •I * hi лаже он и возникает по ходу обсуждения процесса решения, то ответ на не-
- •Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
- •* Последовательность изучения линии уравнений и неравенств
- •I )гапы изучения линии уравнений, неравенств и их систем в основной школе
- •1* Курсе математики 5 класса понятие уравнения трактуется аналогично.
- •Основные классы неравенств изучаются сразу вслед за изучением со- »»I мотствующих классов уравнений.
- •I Ъшить уравнение - это значит найти все его корни или установить, что их нет.
- •Решение квадратных уравнений и неравенств
- •Il Графический метод (I способ)
- •Графический метод
- •Системы уравнений с двумя переменными, в которых одно или оба уравнения второй степени
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Il Графический метод
- •Il Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •Графический метод
- •1. Цели обучения решению текстовых задач
- •2. Пропедевтика алгебраического и геометрического методов решения текстовых задач
- •3. Этапы решения задач на составление уравнений и их реализация
- •Этап {перевод задачи на геометрический язык).
- •Этап (решение задачи на геометрическом языке).
- •1. Из истории введения понятия функциональной зависимости в школьный курс математики
- •2. Различные трактовки понятия функции
- •3. Методика введения понятия функции
- •Этап. Мотивация введетя понятия.
- •Исследовать функцию на основные свойства.
- •Использовать изученные свойства функций при решении различных задач, в частности уравнений и неравенств.
- •Влияние коэффициентов hub на поведение функции
- •Взаимное расположение графиков линейных функции
- •Б. Интеграция аналитического и графического методов в изучении квадратичной функции
- •1. Цели и задачи курса геометрии основной школы
- •2. Содержание обучения геометрии в 7-9 классах
- •3. Логические основы изложения геометрии в 7-9 классах
- •Аксиомы принадлежности
- •Аксиомы порядка
- •Аксиомы измерения отрезков и углов
- •Рекомендуемая литература
- •1. Методика изучения основных свойств простейших геометрических фигур
- •1. Учебник а. В. Погорелова: § 1 «Основные свойства простейших геометрических фигур»,
- •Определения «через ближайший род и видовые отличия»
- •Измерение отрезков и углов
- •3. Учебник а. Д. Александрова и др,: глава I «Начала геометрииж
- •2. Методика формирования геометрических понятий
- •3, Обучение решению задач на первых уроках геометрии
- •II группа
- •1. Различные подходы к формированию понятия равенства фигур
- •Что нужно знать, чтобы утверждать равенство треугольников abc и dek1
- •На рисунке 55 изображено два равных треуголь- ника. Написать равенство этих треугольников, обозначив их вершины.
- •Если разносторонние треугольники abc и dkm
- •11Ри иодом пример.
- •I (сн тральное место в изучении равных треугольников занимают признаём риионота треугольников.
- •Доказательство:
- •Доказательство:
- •Треугольники вас и cdb равны. Напишите все соотношения, из ко- торых следует равенство указанных треугольников.
- •Напишите соотношение между элемен- тами треугольников abc и adc, из которых следовало бы их равенство.
- •Какие методические подходы существуют к введению понятия ранено гва фигур в школьном курсе геометрии? Какой подход, на Ваш взгляд, милмется наиболее удачным?
- •В чем особенности введения понятия равных треугольников в разных учебниках геометрии?
- •Приведите примеры упражнений на усвоение понятия равных треугольников.
- •I. Цели и этапы изучения взаимного расположения прямых на плоскости
- •1 Различные подходы к введению понятия параллельности прямых на плоскости.
- •I. Методика изучения признаков параллельности прямых.
- •1, Цели и этапы изучения взаимного расположения прямых на плоскости
- •2. Различные подходы к введению понятия параллельности прямых на плоскости
- •4. Методические замечания к изучению перпендикулярности прямых на плоскости
- •В данной плоскости через точку вне данной прямой можно провести только одну прямую, параллельную данной.
- •Сумма внутренних углов треугольника равна 2d.
- •1. Различные подходы к изучению многоугольников
- •2. Методика изучения четырехугольников
- •Если в четырехугольнике противоположные стороны попарно равны,
- •Если в четырехугольнике диагонали пересекаются и точкой пересечении делятся пополам, то этот четырехугольник параллелограмм.
- •Какие из систем неравенств задают на плоскости трапецию и почему? Покажите штриховкой множество точек плоскости, заданное системой неравенств:
- •1 H найти площадь трапеции.
- •1, Имеет1 ли ось симметрии фигура, заданная системой неравенств:
- •Верно ли утверждение: а) любой правильный многоугольник является выпуклым; б) любой выпуклый многоугольник является правильным?
- •Чему равны градусные меры углов: а) правильного пятиугольника; б) правильного двенадцатиугольника; в) правильного тридцатишестиугольника?
- •Множество направленных отрезков плоскости.
- •Множество классов направленных отрезков плоскости.
- •Множество параллельных переносов плоскости.
- •Начертите равнобочную трапецию: а) существуют ли векторы, определяемые её вершинами и равные по длине? б) Сколько пар сонаправленных векторов задают вершины трапеции?
- •Сколько пар сонаправленных (противоположно направленных) векторов определяют вершины параллелограмма?
- •Начертить параллелограмм, обозна- чить его вершины и написать все равные ме- жду собой векторы, началом и концом кото- рых являются вершины параллелограмма.
- •Векторы а и ъ равны, что следует из этого?
- •3. Методика изучения действий с векторами
- •II. Умножение вектора на число
- •Учебник геометрии а. В. Погорелова.
- •Учебник геометрии j1. С. Атанасяна и Др.
- •Построить вектор, представляющий сумму
- •4. Методика обучения решению задач с помощью векторов
- •1. Дан многоугольник abcde. Представьте ad в виде суммы: а) двух; б) I рёх; в) четырех векторов, заданных вершинами этого многоугольника.
- •Представьте вектор ав в виде суммы векторов ас, dc , bd .
- •Вектор cDколлинеарен вектору ав и Выразите один век-
- •Четырехугольник abcd - квадрат. Упростите выражение { ав - 3 вс)2,
- •VI. Упражнения на нахождение длины вектора и величины угла между векторами.
- •Какие действия с векторами изучаются в школьном курсе геометрии?
- •Б) в треугольнике лвс известны длины всех сторон. Определить его углы.
- •II кн. До н. Э.) уже фактически пользовался прямоугольными координатами.
- •Простейшие задачи в координатах на плоскости
- •Уравнения фигур на плоскости
- •4. Особенности применения метода координат
- •5. Методика формирования координатного метода решения задач
- •Решение (координатный метод)
- •Iэтап(оптимальный выбор прямоугольной системы координат). Выберем прямоугольную систему координат так, как показано на рис. 93.
- •Этап (перевод задачи на координатный
- •Так как м середина стороны вс, то л/
- •Этап (решение задачи на координат- ном языке).
- •Рекомендуемая литература
- •Значение тригонометрических функций в школьном курсе математики и различные подходы к их изложению
- •I ермипы «косинус», «котангенс» и др. Появились в XI—XVII вв.
- •Этапы изучения линии уравнений, неравенств и их систем в
- •Системы уравнений с двумя переменными, в которых
- •Цели и этапы изучения взаимного расположения прямых на
- •Различные подходы к введению понятии параллельности пря
Решая
первую систему, находим: 0 < х
<
-1
+ /5
.
Решением второй
системы
является промежуток х < 0. Объединяя
оба решения, получаем от-
.
-l
+ Vs
вет:
х < ——-—.
2
В) Решим
неравенство д/l
-
х < х.
Данное
неравенство равносильно системе
неравенств:
f
1
- х > 0,
*
X < х2.
1
+ л[5 .
1
Решая
данную систему, находим: — <х < I.
Ответ:
-lH-Vs
<х<
I.
Укажем
недостатки алгебраического метода
решения. При решении урав-
нения д/l
—
х = х
учащиеся,
найдяХ\
их2,
забывают
сравнить их значения с ОДЗ.
Решая
неравенство д/l-х
> х,
они
испытывают трудности в составлении
сис-
тем неравенств. Составив первую
систему, часто забывают о второй
системе.
Ошибки возникают и при
решении систем.
Построим
в одной системе координат графики
функций^ = д/ 1-х
и
^2
= * (рис. 18).
А)
На геометрическом языке
решить
уравнение д/l
-
х = х
-
это
значит, найти абсциссы точек
пересе-
чения графиков указанных
функций
или установить, что таких
точек нет.
Как
видим из рисунка, корень
уравнения
единственный и он лежит в
интервале
(0; 1). Можно найти его
приближённо по
рисунку, если не
требуется большой
точности, или
найти его аналитически,
решив урав-
нение 1
- х
=
х2,
то
есть х2
+
х
- 1
= 0.
Решение
дает два корня:
_-l
+ Vs -1 - т/5.
Xi
~ —,
х2
= —-.
2
2
Так
как х2
<
0 и не принадлежит интервалу (0; 1), то это
посторонний корень. Как он получается,
можно показать учащимся на рисунке.
Прямая у2
= х
пересекается
с графиком функции уз~
-
д/l
-
х в точке с абсциссой х2
(график
функции^ на рис. изображен пунктиром).
Б-В)
Для решения неравенства д/l-
х
>х (Л/1
-~х: <х) замечаем, что
Графический метод

график
функции у\
= л]
1-х
лежит выше (ниже) графика функции у2
= х на
интервале
х < xi
(xi <
х <
1).
Преимущество
графического метода решения в его
наглядности. Во-
первых, отпадает
необходимость в дополнительных
исследованиях по опре-
делению
постороннего корня х2.
Во-вторых, есть возможность наглядно
по-
казать учащимся, почему в результате
решения уравнения д/l
-
х = х
появля-
ется посторонний корень х2
и почему он отрицательный.
Пример
15. Решить неравенство д/х ^2 £ д/Зх -6.
Решение./.
Алгебраический
метод
Найдем
ОДЗ: \х
- 2 > О,
[Зх-6>0.
Решая
данную систему неравенств, получаем:
х
> 2.
Возведем
обе части неравенства в квадрат:
х
— 2 > Зх - 6,
откуда х < 2.
Сравнивая
полученное решение с ОДЗ, имеем: х = 2.
О
т в е т: х = 2.
Построим
в одной системе координат графики
функцийу\
= д/х - 2
и
у2
=
д/Зх - 6
(рис. 19).
Используя
рисунок, найдем те значения х, при
которых график функ-
ции
у\
расположен не ниже графика функ-
ции
у2-
Очевидно, что при х > 2 функция у\
=
д/х-2
принимает значения, меньшие
значений
функции у2
= д/Зх - 6
(график
функции при х > 2
расположен ниже
графика функции
у2).
При х = 2
значения
функций равны (графики
функций имеют
общую точку).
О
т в е т: х = 2.
2
Пример
16. Решить неравенство Jx-2
+
3 < -.
X
Часто
подходя к решению неравенства формально,
учащиеся преобразуют его и приходят
к неравенству третьей степени х3
- 11х2
+ 12х - 4 < 0, которое они не могут решить
без специальной подготовки.
Данное
неравенство можно решить и методом
оценки его левой и правой частей.
Учитывая ОДЗ: х > 2, замечаем, что левая
часть неравенства всегда больше или
равна 3, а правая - всегда меньше или
равна 1,
а это значит, что левая часть неравенства
не может быть больше правой. Поэтому
получаем ответ: решений нет.
Графический
метод
Построим
в одной системе координат графики
функций:
у\-Jx-2
+
3 иу2
= —
(рис. 20).
х
91
Графический метод

Область
определения первой
функции: х > 2.
Графиком второй
функции является
гипербола. Функ-
ция^ х-
2
+ 3 возрастающая на
всей области
определения (то есть
2
при
х > 2),
а функция у2
=
— убы-
х
вающая
на этом же промежутке.
Графики
функций, как видно из ри-
сунка, не
имеют точек пересечения,
так как
самая нижняя точка графика
функции
ух
есть точка (2;
3), а ветвь
2
гиперболы
у2
= - при х
> 0
располо-
X
жена
ниже координат этой точки.
Ветвь
гиперболы при х
< 0 рассматривать нет смысла, так как
функция ух
при х < 0
не существует.
2
Из
рисунка видно, что график функции у2
= — при х > 2
всегда распо-
Рис.
20
ложен
ниже графика функции у\
=^ х - 2
+ 3, это значит, функция ух
не может принимать значения, большие
значений функции^? поэтому данное
неравенство не имеет решений.
Ответ:
решений нет.
Как
видим, графический метод сопровождается
здесь рассуждениями, обоснованиями
своих выводов, сделанных на основе
рисунка, что положительно сказывается
на развитии мышления учащихся и
предупреждает формализм, присущий
иногда алгебраическому методу решения
подобных неравенств.
Рассмотрим
пример иррационального неравенства,
содержащего корень третьей степени.
Пример
17. Решить неравенство \j
х2
+ 8 >2-х.
Решение./.
Алгебраический
метод
ОДЗ:
х-любое.
Возведем
в куб обе части неравенства и преобразуем
его:
х2
+ 8 > 8 - 12х + 6х2
- х3,
х3
- 5х2+
12х
> 0, х(х2
- 5х + 12) > 0.
Разложим
на множители квадратный трехчлен х2
- 5х + 12. Для этого решим уравнение х2
- 5х + 12 = 0. Дискриминант уравнения Д = 25
- 48 = -23, -23
0,
значит, трехчлен х2
- 5х + 12 > 0 при любом значении х (ветви
параболы нааправлены вверх, и она не
пересекается с осью ОХ).
Так
как х2
— 5х + 12 > 0 при любом х, то решением
неравенства
х(х2
-
5х
+
12)
> 0 будет
промежуток х
> 0.
О т
в е т: х > 0.
92
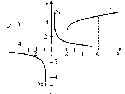
V У* \4- |
1 л |
|
|
1 | 1 2 1 ~ 1 |
1 1 «V t 1 • 1 1 |
1 1 1 1 ^ л -4 2 0. Рис |
1 1 L 1 tO 4^- Ю |
1.
Построим в одной системе коор-
динат
графики функций (рис. 21)
У1
=
\]x?+S
иу2
= 2-
-X.
Графиком
первой функции являет-
ся кривая,
симметричная относительно
оси OY,
с
вершиной в точке (0; 2). Гра-
фиком
второй функции является прямая,
проходящая
через точку (0;
2).
2.
Из рисунка видно, что график
функции
у\
расположен выше прямой
у2
~ 2
— х при х>0
.
Отв
ет:х>0.
Интеграция
алгебраического и
геометрического
(графического) мето-
дов
особенно необходима при решении
иррациональных уравнений и нера-
венств
с параметром. Здесь она часто выступает
в виде единства, слияния
данных:
методов в одном методе. Приведем пример.
Пример
18. Решить неравенство х
- ^ а-х2
>
1.
Решение.
Графический
метод
Преобразуем
данное неравенство к виду х - 1 > у[а-
х2
.
Построим
в одной системе координат графики
функций: у\=х-
1 и
У2
х2.
Графиком первой функции является
прямая, графиком второй
функции
- полуокружность (расположенная в
верхней полуплоскости) с центром в
точке х = 0
и радиусом Ja
(рис.
22).
Очень
важно построить на одном и том же чертеже
график у2
при
различных значениях параметра а.
Тогда легко заметить, что графики у\
и у2
пересекаются, т.е. данное уравнение
имеет действительное решение х0,
если а>
1.
Если
а~
1, то решение х0
= 1 и оно единственно.
Если
а
>
1, решение уравнения также единственно
и оно лежит в интервале (1;
Ja).
Решением
данного неравенства являются те значения
х, при которых график функции ух
(прямая) лежит выше графика функции у2
(полуокружности). Рисунок показывает,
что х0
< х < .
Решив
уравнение
==
:
- д/ а
- х2
—
1,
получаем
два корня: Х\
= , я2
= — . х2
- посторонний ко-
\
+ ^2a-l
_
l-^2a-l
,Х2
2
рень,
так как он не входит в интервал (1; /я).
Итак, решением данного нера венства
является промежуток [-+-
—-,-у[а].
Следует заметить, что с увеличением
а
он увеличивается.
Графический
метод в данном случае содержит в себе
и элементы аналитического метода
(решение уравнения). Он требует от
учащихся более высокого уровня
образного мышления, умение представить
графическую модель в динамике в
зависимости от изменений параметра а.
Ещё
большую эффективность графический
метод имеет при решении уравнений и
неравенств, содержащих модуль. Рассмотрим
этот вопрос подробнее.
4
Уравнения и неравенства, содержащие
модуль
В
школьном курсе математики часто
встречаются уравнения и неравенства,
содержащие переменную под знаком
абсолютной величины (под знаком модуля).
Для решения таких уравнений и неравенств
необходимо разбить числовую ось на
отдельные промежутки так, чтобы на
каждом из них можно было записать
уравнение (неравенство), не используя
знака абсолютной величины.
Аналитический
метод решения уравнений и неравенств,
содержащих модуль, требует часто
утомительных рассмотрений уравнения
или неравенства на интервалах
знакопостоянства функций, стоящих под
знаком модуля. Причем, полученный на
каждом интервале результат необходимо
постоянно проверять, входит он в заданный
интервал или нет (что часто забывают
делать учащиеся). Поэтому наиболее
эффективен при решении подобных
уравнений и неравенств графический
метод. Обучение при этом целесообразно
вести одновременно аналитическому и
графическому методам, что позволит
проводить их сравнение, выбор среди
них наиболее рационального. Графический
метод будет способствовать к тому же
осознанию и осмыслению решений
уравнения (неравенства), полученных
аналитическим путем.
Начинать
обучение следует с решения простейших
уравнений и неравенств, содержащих
модули, предварительно познакомив
учащихся с построением графиков
функций у
= \ х \,
у = \ fa
+
b
\,
у = \ ах2
+ Ьх + с \ и др.
Рассмотрим
примеры.
Пример
19. Решить уравнение | Зх
+ 21
=
1.
Решение./.
Алгебраический
метод
Приравняем
к нулю выражение, стоящее под знаком
модуля:
Зх
+ 2 = 0, откудах
=
2
Разобьем
всю числовую ось на два промежутка
(-оо;--)и(--;+оо).
94
