
- •Алгебра Підручник для 7 класу
- •Юні друзі!
- •§ 1. Рівняння
- •1. Поняття рівняння
- •Приклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •2. Розв’язування рівнянь. Властивості рівнянь
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •3. Лінійні рівняння з однією змінною
- •Підсумок
- •Д ля тих, хто хоче знати більше Рівняння з модулями
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •4. Розв’язування задач за допомогою рівнянь
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 1
- •Завдання для самоперевірки № 1
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 2. Цілі вирази
- •5. Вирази зі змінними. Цілі вирази
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •6. Тотожно рівні вирази. Тотожності
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 2
- •Завдання для самоперевірки № 2
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 3. Одночлени
- •7. Степінь з натуральним показником
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •8. Властивості степеня з натуральним показником
- •1. Множення степенів з однаковими основами.
- •2. Ділення степенів з однаковими основами.
- •3. Піднесення степеня до степеня.
- •4. Піднесення добутку до степеня.
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •9. Одночлен та його стандартний вигляд
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 3
- •Завдання для самоперевірки № 3
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 4. Многочлени
- •10. Многочлен та його стандартний вигляд
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •11. Додавання і віднімання многочленів
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •12. Множення одночлена на многочлен
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •13. Множення многочлена на многочлен
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •14. Розкладання многочленів на множники способом винесення спільного множника за дужки
- •П риклади розв’язання вправ
- •Р івень а
- •Рівень б
- •Р івень в
- •Вправи для повторення
- •15. Розкладання многочленів на множники способом групування
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 4
- •Завдання для самоперевірки № 4
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 5. Формули скороченого множенея
- •16. Множення різниці двох виразів на їх суму
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •17. Квадрат суми і квадрат різниці двох виразів
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •18. Розкладання на множники різниці квадратів двох виразів
- •П риклади розв’язання вправ
- •Р івень а
- •Рівень б
- •Р івень в
- •Вправи для повторення
- •19. Розкладання многочленів на множники з використанням формул квадрата суми і квадрата різниці
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •20. Різниця і сума кубів двох виразів
- •П риклади розв’язання вправ
- •Рівень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •21. Застосування кількох способів для розкладання многочленів на множники
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Д ля тих, хто хоче знати більше
- •22. Застосування перетворень виразів
- •1. Порівняння значень многочлена з нулем.
- •2. Знаходження найбільшого і найменшого значень виразів.
- •3. Розв’язування задач на подільність.
- •4. Знаходження значень многочлена за допомогою мікрокалькулятора.
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 5
- •Завдання для самоперевірки № 5
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 6. Функції
- •23. Функція. Способи задання функції
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •24. Графік функції. Функція як математична модель реальних процесів
- •П риклади розв’язання вправ
- •Р івень а
- •Рівень б
- •Р івень в
- •Вправи для повторення
- •25. Лінійна функція
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 6
- •Завдання для самоперевірки № 6
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 7. Системи лінійних рівнянь із двома змінними
- •26. Рівняння із двома змінними
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •27. Графік лінійного рівняння із двома змінними
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •28. Системи двох лінійних рівнянь із двома змінними
- •1. Системи лінійних рівнянь із двома змінними та їх розв’язки.
- •2. Розв’язування систем лінійних рівнянь графічним способом.
- •П риклади розв’язання вправ
- •29. Розв’язування систем лінійних рівнянь способом підстановки
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •30. Розв’язування систем лінійних рівнянь способом додавання
- •Д ля тих, хто хоче знати більше
- •Вправи для повторення
- •31. Розв’язування задач за допомогою систем рівнянь
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 7
- •Завдання для самоперевірки № 7
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •Задачі за курс алгебри 7 класу
- •Задачі підвищеної складності До § 1. Лінійні рівняння з однією змінною
- •До § 2. Цілі вирази
- •До § 3. Одночлени
- •До § 4. Многочлени
- •До § 5. Формули скороченого множення
- •До § 6. Функції
- •До § 7. Системи лінійних рівнянь із двома змінними
- •Логічні задачі
- •Вітчизняні математики
- •Відомості з курсу математики 5–6 класів Подільність натуральних чисел
- •Найбільший спільний дільник
- •Найменше спільне кратне
- •Десяткові дроби
- •Звичайні дроби
- •Додатні та від’ємні числа
- •Відповіді
- •Завдання для самоперевірки № 1
- •Завдання для самоперевірки № 2
- •Завдання для самоперевірки № 3
- •Завдання для самоперевірки № 4
- •Завдання для самоперевірки № 5
- •Завдання для самоперевірки № 6
- •Завдання для самоперевірки № 7
- •Задачі за курс алгебри 7 класу
- •Задачі підвищеної складності
- •Предметний покажчик
- •Розділ і. Лінійні рівняння з однією змінною
- •Розділ іі. Цілі вирази
- •Розділ ііі. Функції
- •§ 6. Функції
- •Розділ іv. Системи лінійних рівнянь із двома змінними
- •§ 7. Системи лінійних рівнянь із двома змінними
- •Навчальне видання
- •Алгебра
- •46010, М. Тернопіль, вул. Поліська, 6а. Тел. 8-(0352)-43-10-31, 43-15-15, 43-10-21.
Додатні та від’ємні числа
22. Модулем додатного числа і нуля є це ж число; модулем від’ємного числа є протилежне йому число:

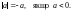
Наприклад: 5,3 = 5,3; 0 = 0; –1,8 = 1,8.
23. Щоб додати два від’ємних числа, потрібно додати їх модулі й поставити перед отриманим числом знак «–».
Щоб додати два числа з різними знаками, потрібно знайти модулі чисел, від більшого модуля відняти менший модуль і поставити перед отриманим числом знак того доданка, модуль якого більший.
Наприклад:
–1,6 + (–2,3) = –3,9; –0,7 + 0,7 = 0; 3,2 + (–4,7) = –(4,7 – 3,2) = –1,5.
24. Щоб від одного числа відняти інше, досить до зменшуваного додати число, протилежне від’ємнику.
Наприклад: –15 – (–9) = –15 + 9 = –6.
25. Щоб знайти добуток двох від’ємних чисел, досить перемножити модулі цих чисел.
Щоб знайти добуток двох чисел з різними знаками, досить перемножити їх модулі і поставити перед одержаним числом знак «–».
Наприклад: (–1,1) · (–0,9) = 1,1 · 0,9 = 0,99;
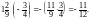
26. Щоб знайти частку двох від’ємних чисел, досить поділити модуль діленого на модуль дільника.
Щоб знайти частку чисел з різними знаками, досить поділити модуль діленого на модуль дільника і поставити перед одержаним числом знак «–».
Наприклад: –105 : (–21) = 105 : 21 = 5;
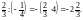
27. Щоб розкрити дужки, перед якими стоїть знак «+», потрібно опустити дужки і знак «+», що стоїть перед ними, і записати всі доданки, які були в дужках, зі своїми знаками:
a + (–b + c) = a – b + c.
Щоб розкрити дужки, перед якими стоїть знак «–», потрібно опустити дужки і знак «–», що стоїть перед ними, і записати всі доданки, які були в дужках, з протилежними знаками:
a – (b – c) = a – (+b – c) = a – b + c.
28. Щоб звести подібні доданки, потрібно додати їх коефіцієнти і результат помножити на спільну буквену частину.
Наприклад: 7a – 9a + 4a = (7 – 9 + 4)a = 2a.
Відповіді
§ 1
15. a = 3.
16. a = 23.
17. Вказівка.
Обґрунтуйте, що для х = 2
значення лівої частини рівняння є
непарним числом. 20. 375 грн.
21. 148 т.
32. а) 16;
б) 1,125;
в)  г)
г) 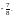 33. а) 0,2;
б)
33. а) 0,2;
б) 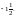 34. а) –1;
б)
34. а) –1;
б) 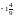 35. а)
35. а) 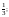 б) 6.
36. а) –3;
–2;
–1;
б) 0;
1; 2; 3;
б) 6.
36. а) –3;
–2;
–1;
б) 0;
1; 2; 3;
 39. а) 54 080 жителів;
б) 50 000 жителів.
48. а) 2;
б) 35;
в) 10,2;
г) 4.
49. а) 2;
б) 0,7;
в) 0,1;
г) 6.
50. а) 5;
б) 2,5;
в) 2,5;
г) 3,5;
д) 4;
е) коренів
немає. 51. 0.
52. 4. 53. 3.
54. а) 1;
б) 5;
в) 2;
г) коренем
рівняння є будь-яке число. 55. а)
39. а) 54 080 жителів;
б) 50 000 жителів.
48. а) 2;
б) 35;
в) 10,2;
г) 4.
49. а) 2;
б) 0,7;
в) 0,1;
г) 6.
50. а) 5;
б) 2,5;
в) 2,5;
г) 3,5;
д) 4;
е) коренів
немає. 51. 0.
52. 4. 53. 3.
54. а) 1;
б) 5;
в) 2;
г) коренем
рівняння є будь-яке число. 55. а)  б)
б) 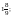 в)
в) 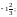 г) 0.
56. а) 10;
б) 1;
в) 8;
г)
г) 0.
56. а) 10;
б) 1;
в) 8;
г) 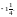 57. г) –2;
9; д) 2,5;
5; е)
57. г) –2;
9; д) 2,5;
5; е) 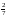 .
58. а) –4;
4; б) –2;
2; в) коренів
немає. 59. а) –4;
4; б) –5;
11; в) коренів
немає; г) 7;
д) –3;
3; е) –16;
16. 60. а) 1;
б)
.
58. а) –4;
4; б) –2;
2; в) коренів
немає. 59. а) –4;
4; б) –5;
11; в) коренів
немає; г) 7;
д) –3;
3; е) –16;
16. 60. а) 1;
б)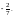 61. а) 8; 12;
б) 6; 2;
в) 1; 1;
г) 0,5;
1,5. 62. а) 5;
б) –3;
2; в) 4;
г) коренів
немає; д) коренем
рівняння є будь-яке недодатне число;
е) коренем
рівняння є будь-яке невід’ємне число.
63. а) 0;
б) коренів
немає; в) коренів
немає. 64. 19.
69. 30 яблук.
70. 40 кг;
28 кг. 71. 18
і 15 комп’ютерів. 72. 784 га;
224 га. 73. 36
і 12 років. 74. 16
і 20 деталей. 75. 300 сторінок.
76. 90 км.
77. а) 9 см; 6 см; 10 см;
б) 10,5 см;
5,5 см; 9 см. 78. Олег
— 2 грн.; Сергій — 6 грн.; Віталій
— 4 грн. 79. 130 кг;
150 кг; 180 кг. 80. 52,5 кг;
45 кг; 37,5 кг. 81. 20 км/год;
16 км/год; 12 км. 82. 66
і 54 яблук. 83. 400 км.
84. 200 км.
85. 30 км.
86. 21 км/год.
87. 40 км.
88. 56 км/год;
60 км/год. 89. 56,
14 і 11 років. 90. 60
і 35 книжок. 91. 80 семи-
класників.
92. 90 деталей.
93. 350 грн.
94. 10 хв;
40 хв. 95. 28 учнів.
96. 8 ц,
2 ц. 97. 40 л;
30 л. 98. 500 г.
99. 38 т.
102. 34.
105. 30 способами.
109. в) 2;
г) 5;
д) 2,6;
е) 4.
110. а) 5;
б) 1.
111. а) коренів
немає; б) 2;
2. 112. а) 0;
4; б) 2;
1. 113. а) 7;
б) –0,6.
114. а = 0.
115. Не
існує. 116. 108 см2.
117. 8 см;
12 см; 10 см. 118. 70 га.
119. 15 км.
120. 1,2 год.
121. 3 кг;
7 кг. 122. 40 л.
61. а) 8; 12;
б) 6; 2;
в) 1; 1;
г) 0,5;
1,5. 62. а) 5;
б) –3;
2; в) 4;
г) коренів
немає; д) коренем
рівняння є будь-яке недодатне число;
е) коренем
рівняння є будь-яке невід’ємне число.
63. а) 0;
б) коренів
немає; в) коренів
немає. 64. 19.
69. 30 яблук.
70. 40 кг;
28 кг. 71. 18
і 15 комп’ютерів. 72. 784 га;
224 га. 73. 36
і 12 років. 74. 16
і 20 деталей. 75. 300 сторінок.
76. 90 км.
77. а) 9 см; 6 см; 10 см;
б) 10,5 см;
5,5 см; 9 см. 78. Олег
— 2 грн.; Сергій — 6 грн.; Віталій
— 4 грн. 79. 130 кг;
150 кг; 180 кг. 80. 52,5 кг;
45 кг; 37,5 кг. 81. 20 км/год;
16 км/год; 12 км. 82. 66
і 54 яблук. 83. 400 км.
84. 200 км.
85. 30 км.
86. 21 км/год.
87. 40 км.
88. 56 км/год;
60 км/год. 89. 56,
14 і 11 років. 90. 60
і 35 книжок. 91. 80 семи-
класників.
92. 90 деталей.
93. 350 грн.
94. 10 хв;
40 хв. 95. 28 учнів.
96. 8 ц,
2 ц. 97. 40 л;
30 л. 98. 500 г.
99. 38 т.
102. 34.
105. 30 способами.
109. в) 2;
г) 5;
д) 2,6;
е) 4.
110. а) 5;
б) 1.
111. а) коренів
немає; б) 2;
2. 112. а) 0;
4; б) 2;
1. 113. а) 7;
б) –0,6.
114. а = 0.
115. Не
існує. 116. 108 см2.
117. 8 см;
12 см; 10 см. 118. 70 га.
119. 15 км.
120. 1,2 год.
121. 3 кг;
7 кг. 122. 40 л.
